1.4 三角函数的图像与性质
一、选择题：
1．满足tanα≥cotα的角的一个取值区间是（ ）
A.(0, ) B. [0,] C. [,] D. [,]
2．函数的定义域是（ ）
A.{xx≠, x∈R} B. {xx≠,x∈R}
C. {xx≠kπ +,x∈R} D. {xx≠kπ +,x∈R}
3．下列函数中周期为的奇函数是（ ）
A.y=cos(2x+) B.y=tan C.y=sin(2x+) D.y= - cotx
4．若sinα>tanα>cotα(-<x<)，则α的取值范围是（ ）
A.(- ,) B. (-,0) C.(0, ) D.( ,)
二、填空题
5．比较大小：tan222°_________tan223°.
6．函数y=tan(2x+)的单调递增区间是__________．
7．函数 y=sinx 与 y=tanx 的图象在区间[0，2π]上交点的个数是________．
8．函数 y=f(x) 的图象右移，横坐标缩小到原来的一半，得到y=tan2x的图象，
则y=f(x)解析式是_______________．
9．函数y=lg的奇偶性是__________．
10．函数的y=tan(2x-)周期是___________．
三、解答题
11．作函数y=cotxsinx的图象.
12．作出函数y=tanx的图象，并根据图象求其单调区间
13． 求函数y=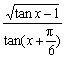
的定义域.
14． 求下列函数的值域：
（1）y=2cos2x+2cosx－1；
（2）y=
.
15．求函数y=3tan（
－
）的周期和单调区间.
参考答案
一、选择题：
1.C 2.D 3.C 4.B
二 、填空题：
5．< 6.( kπ+, kπ+) (k∈Z) 7. 5
8. y=tan(x+) 9. 奇函数 10.
三、解答题
11．分析：首先将函数的解析式变形，化为最简形式，然后作函数的图象.
解：当sinx≠0，即x≠kπ（k∈Z）时，有y=cotxsinx=cosx，即y=cosx（x≠kπ，k∈Z）.其图象如下图.
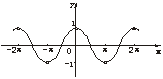
12．解：由于y=tanx=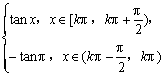
（k∈Z），
所以其图象如图所示，单调增区间为［kπ，kπ+
］（k∈Z）；单调减区间为（kπ－，kπ）（k∈Z）.
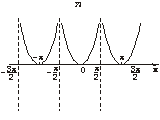
13．解：根据自变量x满足的条件列出不等式组，解之即可.
由题意得
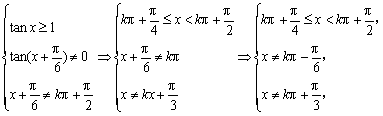
所以定义域为［kπ+
，kπ+
）∪（kπ+，kπ+）（k∈Z）.
14．解：（1）y=2（cosx+
）2－
.
将其看作关于cosx的二次函数，注意到－1≤cosx≤1，
∴当cosx=－时，ymin=－；
当cosx=1时，ymax=3.
∴y∈［－，3］.
本题结合了二次函数求最值这一知识，但应注意cosx的取值范围.
（2）由原式得cosx=
.
∵－1≤cosx≤1，∴－1≤≤1.
∴y≥3或y≤
.
∴值域为{yy≥3或y≤}.
15．解：y=3tan（－）=－3tan（－），
∴T=
=4π.
由kπ－＜－＜kπ+（k∈Z）得
4kπ－
＜x＜4kπ+
（k∈Z）.
∵3tan（－）在（4kπ－，4kπ+）（k∈Z）内单调递增，
∴y=－3tan（－）在（4kπ－，4kπ+）（k∈Z）内单调递减.
故原函数的周期为4π，递减区间为（4kπ－，4kπ+）（k∈Z）.