高三年级数学(理科)第一次调研考试
2008.3
一、 选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个备选项中,有且只有一项是符合要求的.
1.
设全集![]() ,集合
,集合![]() ,集合
,集合![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.
复数![]() ,
,![]() ,则复数
,则复数![]() 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.
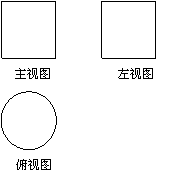 如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 ( )
如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
4.
设![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.
已知等差数列![]() 的公差
的公差![]() ,它的第1、5、17项顺次成等比数列,则这个等比数列的公比是 ( )
,它的第1、5、17项顺次成等比数列,则这个等比数列的公比是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.
函数![]() 的零点所在的大致区间是 ( )
的零点所在的大致区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.
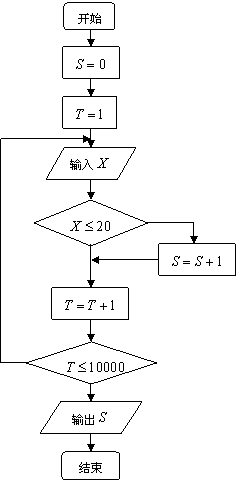
为调查深圳市中学生平均每人每天参加体育锻炼时间![]() (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是 ( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是 ( )
A.3800 B.6200 C.![]() D.
D.![]()
 |
8.
如图,已知![]() 、
、![]() ,从点
,从点![]() 射出的光线经直线
射出的光线经直线![]() 反向后再射到直线
反向后再射到直线![]() 上,最后经直线
上,最后经直线![]() 反射后又回到
反射后又回到![]() 点,则光线所经过的路程是 ( )
点,则光线所经过的路程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

二、 填空题:本大题共7小题,每小题5分,共30分.其中13~15小题是选做题,考生只能选做两题,若三题全答,则只计算前两题得分.
9.
在![]() 中,
中,![]() 、
、![]() 分别为角
分别为角![]() 、
、![]() 的对边,若
的对边,若![]() ,
,![]() ,
,![]() ,则边
,则边![]() 的长等于 .
的长等于 .
10. 某高三学生希望报名参加某6所高校中的3所学校的自主招生考试,由于其中两所学校的考试时间相同,因此该学生不能同时报考这两所学校.该学生不同的报考方法种数是
.(用数字作答)
11.
在![]() 中,两直角边分别为
中,两直角边分别为![]() 、
、![]() ,设
,设![]() 为斜边上的高,则
为斜边上的高,则![]() ,由此类比:三棱锥
,由此类比:三棱锥![]() 中的三条侧棱
中的三条侧棱![]() 、
、![]() 、
、![]() 两两垂直,且长度分别为
两两垂直,且长度分别为![]() 、
、![]() 、
、![]() ,设棱锥底面
,设棱锥底面![]() 上的高为
上的高为![]() ,则 .
,则 .
12.
 已知定义在区间
已知定义在区间![]() 上的函数
上的函数![]() 的图像如图所示,对于满足
的图像如图所示,对于满足![]() 的任意
的任意![]() 、
、![]() ,给出下列结论:
,给出下列结论:
①
![]() ;
;
②
![]() ;
;
③
![]() .
.
其中正确结论的序号是 .(把所有正确结论的序号都填上)
13.
(坐标系与参数方程选做题)在极坐标系中,圆![]() 的圆心的极坐标是 ,它与方程
的圆心的极坐标是 ,它与方程![]() (
(![]() )所表示的图形的交点的极坐标是 .
)所表示的图形的交点的极坐标是 .
14.
(不等式选讲选做题)已知点![]() 是边长为
是边长为![]() 的等边三角形内一点,它到三边的距离分别为
的等边三角形内一点,它到三边的距离分别为![]() 、
、![]() 、
、![]() ,则
,则![]() 、
、![]() 、
、![]() 所满足的关系式为 ,
所满足的关系式为 ,![]() 的最小值是 .
的最小值是 .
15.
(几何证明选讲选做题)如图,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 的平分线分别交直线
的平分线分别交直线![]() 、
、![]() 于
于![]() 、
、![]() 两点,已知
两点,已知![]() ,
,![]() ,则
,则![]() ,
,![]() .
.

三、 解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
16. (本小题满分12分)
已知向量![]() ,
,![]() ,函数
,函数![]() .
.
(Ⅰ)求![]() 的最大值及相应的
的最大值及相应的![]() 的值;
的值;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
17. (本小题满分12分)
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在
下落的过程中,将3次遇到黑色障碍物,最后落入![]() 袋或
袋或![]() 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是![]() .
.
(Ⅰ)求小球落入![]() 袋中的概率
袋中的概率![]() ;
;
(Ⅱ)在容器入口处依次放入4个小球,记![]() 为落入
为落入![]() 袋中的小球个数,试求
袋中的小球个数,试求![]() 的概率和
的概率和![]() 的数学期望
的数学期望![]() .
.

18. (本小题满分14分)
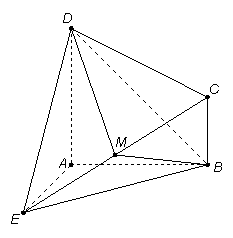
如图所示的几何体![]() 中,
中,![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,
![]() ,
,![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
19. (本小题满分14分)
在平面直角坐标系中,已知点![]() 、
、![]() ,
,![]() 是平面内一动点,直线
是平面内一动点,直线![]() 、
、
![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
20. (本小题满分14分)
已知![]() ,
,![]() (
(![]() ),直线
),直线![]() 与函数
与函数![]() 、
、![]() 的图像都
的图像都
相切,且与函数![]() 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(Ⅰ)求直线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)若![]() (其中
(其中![]() 是
是![]() 的导函数),求函数
的导函数),求函数![]() 的最大值;
的最大值;
(Ⅲ)当![]() 时,求证:
时,求证:![]() .
.
21. (本小题满分14分)
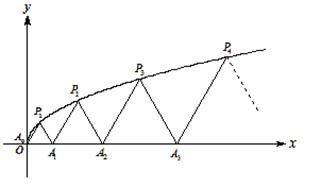
如图,![]() 、
、![]() 、…、
、…、![]() (
(![]() )是曲线
)是曲线![]() :
:![]()
(![]() )上的
)上的![]() 个点,点
个点,点![]() (
(![]() )在
)在![]() 轴的正半轴上,且
轴的正半轴上,且![]() 是正三角形(
是正三角形(![]() 是坐标原点).
是坐标原点).
(Ⅰ)写出![]() 、
、![]() 、
、![]() ;
;
(Ⅱ)求出点![]() (
(![]() )的横坐标
)的横坐标![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅲ)设![]() ,若对任意的正整数
,若对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
高三年级数学(理科)第一次调研考试
数学(理科)参考答案
一、 选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个备选项中,有且只有一项是符合要求的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | A | A | C | B | B | C | A |
二、 填空题:本大题共7小题,每小题5分,共30分.其中13~15小题是选做题,考生只能选做两题,若三题全答,则只计算前两题得分.
9.![]() 10.
10.![]() 11.
11.![]()
12.②③ 13.![]() ,
,![]()
14.![]() ,
,![]() 15.
15.![]() ,
,![]()
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
16. 解:(Ⅰ)因为![]() ,
,![]() ,所以
,所以
![]()
![]() .
.
因此,当![]() ,即
,即![]() (
(![]() )时,
)时,![]() 取得最大值
取得最大值![]() ;
;
(Ⅱ)由![]() 及
及![]() 得
得![]() ,两边平方得
,两边平方得
![]() ,即
,即![]() .
.
因此,![]() .
.
17. 解:(Ⅰ)记“小球落入![]() 袋中”为事件
袋中”为事件![]() ,“小球落入
,“小球落入![]() 袋中”为事件
袋中”为事件![]() ,则事件
,则事件![]() 的对立事件为
的对立事件为![]() ,而小球落入
,而小球落入![]() 袋中当且仅当小球一直向左落下或一直向右落下,故
袋中当且仅当小球一直向左落下或一直向右落下,故
![]() ,
,
从而![]() ;
;
(Ⅱ)显然,随机变量![]() ,故
,故
![]() ,
,
![]() .
.
18.  解: 建立如图所示的空间直角坐标系,
解: 建立如图所示的空间直角坐标系,
并设![]() ,则
,则
(Ⅰ)![]() ,
,![]() ,
,
所以![]() ,从而得
,从而得
![]() ;
;
(Ⅱ)设![]() 是平面
是平面![]() 的
的
法向量,则由![]() ,
,![]() 及
及
![]() ,
,![]()
得
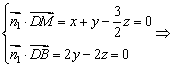 可以取
可以取![]() .
.
显然,![]() 为平面
为平面![]() 的法向量.
的法向量.
设二面角![]() 的平面角为
的平面角为![]() ,则此二面角的余弦值
,则此二面角的余弦值
![]() .
.
19. 解:(Ⅰ)依题意,有![]() (
(![]() ),化简得
),化简得
![]() (
(![]() ),
),
这就是动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)依题意,可设![]() 、
、![]() 、
、![]() ,则有
,则有
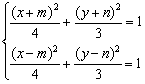 ,
,
两式相减,得 ,由此得点
,由此得点![]() 的轨迹方程为
的轨迹方程为
![]() (
(![]() ).
).
设直线![]() :
:![]() (其中
(其中![]() ),则
),则
![]() ,
,
故由![]() ,即
,即![]() ,解之得
,解之得![]() 的取值范围是
的取值范围是![]() .
.
20. 解:(Ⅰ)依题意知:直线![]() 是函数
是函数![]() 在点
在点![]() 处的切线,故其斜率
处的切线,故其斜率
![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
又因为直线![]() 与
与![]() 的图像相切,所以由
的图像相切,所以由
 ,
,
得![]() (
(![]() 不合题意,舍去);
不合题意,舍去);
(Ⅱ)因为![]() (
(![]() ),所以
),所以
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
因此,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;
;
(Ⅲ)当![]() 时,
时,![]() .由(Ⅱ)知:当
.由(Ⅱ)知:当![]() 时,
时,![]() ,即
,即![]() .因此,有
.因此,有
![]() .
.
21. 解:(Ⅰ)![]() ,
,![]() ,
,![]() ;
;
(Ⅱ)依题意,得![]() ,
,![]() ,由此及
,由此及![]() 得
得
![]() ,
,
即![]() .
.
由(Ⅰ)可猜想:![]() (
(![]() ).
).
下面用数学归纳法予以证明:
(1)当![]() 时,命题显然成立;
时,命题显然成立;
(2)假定当![]() 时命题成立,即有
时命题成立,即有![]() ,则当
,则当![]() 时,由归纳假设及
时,由归纳假设及
![]()
得![]() ,即
,即
![]() ,
,
解之得
![]() (
(![]() 不合题意,舍去),
不合题意,舍去),
即当![]() 时,命题成立.
时,命题成立.
由(1)、(2)知:命题成立.
(Ⅲ)![]()
![]()
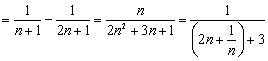 .
.
令![]() (
(![]() ),则
),则![]() ,所以
,所以![]() 在
在![]() 上是增函数,故当
上是增函数,故当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,即当
,即当![]() 时,
时,![]() .
.
![]() (
(![]() ,
,![]() )
)
![]() ,即
,即![]() (
(![]() )
)
![]() .
.
解之得,实数![]() 的取值范围为
的取值范围为![]() .
.