高三数学教学质量检测（一）
数 学 试 题（文科）
本试卷分选择题和非选择题两部分，共4页. 满分150分. 考试时间120分钟.
注意事项：
1.答卷前，考生要务必填写答题卷上的有关项目.
2.选择题每小题选出答案后，用黑色字迹的钢笔或签字笔把答案代号填在答题卷对应的表格内;答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卷的整洁.考试结束后，将答题卷和答题卡交回.
第一部分 选择题（共50分）
一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．
（ ）．
A．
B．
C．
D．
2．已知集合
，则
= （ ）．
A．
B．
C．
D．
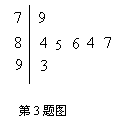
3．如图是
年元旦晚会举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的众数和中位数分别为（ ）．
A．
，
B．，
C．， D．，
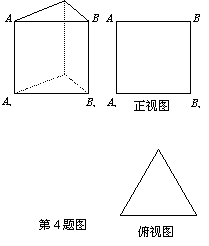
4．如图，三棱柱的棱长为2，底面是边长为2的
正三角形，
，正视图是边长为2的
正方形,则左视图的面积为（ ）．
A. 
B. 
C. 
D. 
5．在平面直角坐标系中，不等式组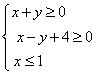
表示的平面区域面积是（ ）．
A．
B．
C． 
D．
6．在△ABC中，角A、B、C的对边分别为
则
（ ）．
A． 1 B. 2
C. —1
D.
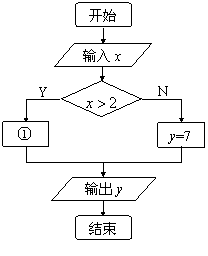
7．在佛山市禅城区和南海区打的士收费办法如下：不超过2公里收7元，超过2.公里的里程每公里收2.6元，另每车次超过2公里收燃油附加费1元（其他因素不考虑）．相应收费系统的流程图如图所示，则①处应填（ ）．
A．
B．
C．
D．
8. 椭圆
的两个焦点为F1、F2，过F1作垂直于x轴的直线与椭圆相交，一个交点为P，则
到F2 的距离为（ ）．
A．
B．
C．
D．4
9. 若数列
满足
（
为正常数，
），则称为“等方差数列”．
甲：数列是等方差数列； 乙：数列是等差数列，则（
）．
A．甲是乙的充分条件但不是必要条件
B．甲是乙的必要条件但不是充分条件
C．甲是乙的充要条件
D．甲既不是乙的充分条件也不是乙的必要条件
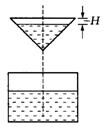10．如图所示，液体从一圆锥形漏斗漏入一圆柱形桶中，开始时，漏斗盛满液体，经过3分钟漏完．已知圆柱中液面上升的速度是一个常量，H是圆锥形漏斗中液面下落的距离，则H与下落时间t（分）的函数关系表示的图象只可能是（ ）．
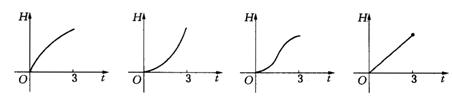
A． B． C． D．
第二部分 非选择题（共100分）
二、填空题（本大题共5小题，其中11—13题是必做题，14—15题是选做题.每小题5分，满分20分）
11．函数
的值域是_________.
12．若三点
共线，则
.
13．观察：
；
； 
；….对于任意正实数
，试写出使
成立的一个条件可以是
____.
▲ 选做题：在下面二道小题中选做一题，二题都选只计算前一题的得分.
14．(坐标系与参数方程)在直角坐标系中圆
的参数方程为
（
为参数），以原点
为极点，以
轴正半轴为极轴建立极坐标系，则圆的圆心极坐标为_________．
|
、
是圆的两条弦，且AB是线段CD的中垂线，已知AB=6，CD=
，则线段AC的长度为 _．
三、解答题（本大题共6题，共80分，解答应写出文字说明、证明过程或演算步骤）
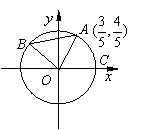16．（本题满分12分）
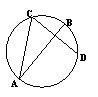
如图A、B是单位圆O上的点，且
在第二象限. C是圆与轴正半轴的交点，A点的坐标为
，△AOB为正三角形.
（Ⅰ）求
；
|
.
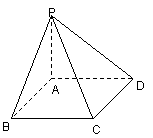17、（本题满分12分）
如图，四棱锥
的底面是边长为1的正方形，
（Ⅰ）求证:
平面
；
|
的体积.
18.（本小题满分14分）
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图，解答下列问题：
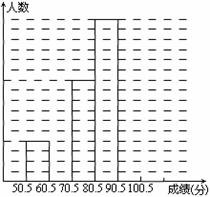
（Ⅰ）填充频率分布表的空格(将答案直接填在表格内)；
（Ⅱ）补全频数条形图；
（Ⅲ）若成绩在75.5~85.5分的学生为二等奖，问获得二等奖的学生约为多少人？
19．（本小题满分14分）
抛物线
的准线的方程为
，该抛物线上的每个点到准线的距离都与到定点N的距离相等，圆N是以N为圆心，同时与直线
相切的圆，
（Ⅰ）求定点N的坐标；
（Ⅱ）是否存在一条直线
同时满足下列条件：
① 分别与直线
交于A、B两点，且AB中点为
；
② 被圆N截得的弦长为2；
20．（本小题满分14分）
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
… … … …
… … … … …
假设第
行的第二个数为
，
（Ⅰ）依次写出第六行的所有个数字；
（Ⅱ）归纳出
的关系式并求出
的通项公式；
（Ⅲ）设
求证：
…
21．（本小题满分14分）
已知函数
取得极小值
.
（Ⅰ）求a，b的值；
（Ⅱ）设直线
. 若直线l与曲线S同时满足下列两个条件：
（1）直线l与曲线S相切且至少有两个切点；
（2）对任意x∈R都有
. 则称直线l为曲线S的“上夹线”.
试证明：直线
是曲线
的“上夹线”.
高三数学教学质量检测（一）
数学试题（文科）参考答案和评分标准
一、选择题（每题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | A | B | D | B | D | C | D | B |
二、填空题（每题5分，共20分,两空的前一空3分，后一空2分）
11．
12．4
13．
14．
15. 
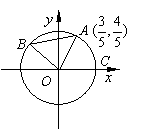三、解答题（本大题共6小题，共80分）
16．（本题满分12分）
如图A、B是单位圆O上的点，且在第二象限. C是圆与轴正半轴的交点，A点的坐标为，△AOB为正三角形.
（Ⅰ）求；
（Ⅱ）求.
|
，根据三角函数定义可知
---4分
（2）因为三角形AOB为正三角形，所以
，
，
，
-----------------------------6分
所以=
-------------------------10分
=
.
--------------------------------------12分
17、（本题满分12分）
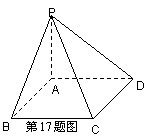如图，四棱锥的底面是边长为1的正方形，
（Ⅰ）求证:平面；
（Ⅱ）求四棱锥的体积.
（Ⅰ）因为四棱锥的底面是边长为1的正方形，
所以
，所以
------------4分
又
，
所以平面
--------------------------------------8分
（Ⅱ）四棱锥的底面积为1，
因为平面，所以四棱锥的高为1，
所以四棱锥的体积为
.
--------------------12分
18.（本小题满分14分）
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图，解答下列问题：
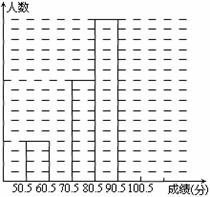
（Ⅰ）填充频率分布表的空格(将答案直接填在表格内)；
（Ⅱ）补全频数条形图；
（Ⅲ）若成绩在75.5~85.5分的学生为二等奖，问获得二等奖的学生约为多少人？
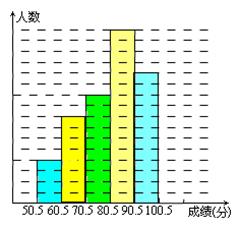解：(1)
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | 0.24 |
| 合计 | 50 | 1.00 |
---------------------4分
(2) 频数直方图如右上所示--------------------------------8分
(3) 成绩在75.5~80.5分的学生占70.5~80.5分的学生的
，因为成绩在70.5~80.5分的学生频率为0.2 ，所以成绩在76.5~80.5分的学生频率为0.1 ，---------10分
成绩在80.5~85.5分的学生占80.5~90.5分的学生的
，因为成绩在80.5~90.5分的学生频率为0.32 ，所以成绩在80.5~85.5分的学生频率为0.16 -------------12分
所以成绩在76.5~85.5分的学生频率为0.26，
由于有900名学生参加了这次竞赛，
所以该校获得二等奖的学生约为0.26´900=234（人） ------------------14分
19．（本小题满分14分）
抛物线的准线的方程为，该抛物线上的每个点到准线的距离都与到定点N的距离相等，圆N是以N为圆心，同时与直线 相切的圆，
（Ⅰ）求定点N的坐标；
（Ⅱ）是否存在一条直线同时满足下列条件：
① 分别与直线交于A、B两点，且AB中点为；
② 被圆N截得的弦长为2；
解：（1）因为抛物线的准线的方程为
所以
，根据抛物线的定义可知点N是抛物线的焦点，
-----------2分
所以定点N的坐标为
----------------------------3分
（2）假设存在直线满足两个条件，显然斜率存在，
-----------4分
设的方程为
，
------------------------5分
以N为圆心，同时与直线 相切的圆N的半径为
， ----6分
方法1：因为被圆N截得的弦长为2，所以圆心到直线的距离等于1， -------7分
即
，解得
，
-------------------------------8分
当
时，显然不合AB中点为的条件，矛盾！
--------------9分
当
时，的方程为
----------------------------10分
由
，解得点A坐标为
，
------------------11分
由
，解得点B坐标为
，
------------------12分
显然AB中点不是，矛盾！
----------------------------------13分
所以不存在满足条件的直线．
------------------------------------14分
方法2：由
，解得点A坐标为
，
------7分
由
，解得点B坐标为
， ------------8分
因为AB中点为，所以
，解得
， ---------10分
所以的方程为
，
圆心N到直线的距离
，
-------------------------------11分
因为被圆N截得的弦长为2，所以圆心到直线的距离等于1，矛盾！ ----13分
所以不存在满足条件的直线．
-------------------------------------14分
方法3：假设A点的坐标为
，
因为AB中点为，所以B点的坐标为
，
-------------8分
又点B 在直线
上，所以
，
----------------------------9分
所以A点的坐标为
，直线的斜率为4，
所以的方程为，
-----------------------------10分
圆心N到直线的距离，
-----------------------------11分
因为被圆N截得的弦长为2，所以圆心到直线的距离等于1，矛盾！ ---------13分
所以不存在满足条件的直线．
----------------------------------------14分
20．（本小题满分14分）
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
… … … …
… … … … …
假设第行的第二个数为，
（Ⅰ）依次写出第六行的所有个数字；
（Ⅱ）归纳出的关系式并求出的通项公式；
（Ⅲ）设求证：
解：（1）第六行的所有6个数字分别是6，16，25，25，16，6； --------------2分
（2）依题意
，
-------------------------------5分
------------------------7分
，
所以
； -------------------------------------9分
（3）因为所以
-------------11分
---14分
21．（本小题满分14分）
已知函数取得极小值.
（Ⅰ）求a，b的值；
（Ⅱ）设直线. 若直线l与曲线S同时满足下列两个条件：（1）直线l与曲线S相切且至少有两个切点；（2）对任意x∈R都有. 则称直线l为曲线S的“上夹线”.
试证明：直线是曲线的“上夹线”.
解：（I）因为
，所以
---------------1分
，
-------------------------------2分
解得
，
--------------------------------------------------------------------3分
此时
，
当
时
，当
时
，
-------------------------5分
所以
时
取极小值，所以符合题目条件；
----------------6分
（II）由
得
，
当
时，，此时
，
，
，所以
是直线与曲线
的一个切点；
-----------8分
当
时，，此时
，
，
，所以
是直线与曲线的一个切点；
-----------10分
所以直线l与曲线S相切且至少有两个切点；
对任意x∈R，
，
所以
---------------------------------------------------------------------13分
因此直线是曲线的“上夹线”.
----------14分