北京市西城区2001年抽样测试高三数学试卷（文科）
2001.5
学校_______ ____ 班级________ ___ 姓名 _____ ______
| 题号 | 一 | 二 | 三 | 总分 | |||||
| （17） | （18） | （19） | （20） | （21） | （22） | ||||
| 分数 | |||||||||
一、选择题：本大题共12小题；每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合要求的。每小题选出答案后，用铅笔在下表中将对应答案标号涂黑。
| 题 号 | （1） | （2） | （3） | （4） | （5） | （6） | （7） | （8） | （9） | （10） | （11） | （12） |
| 答 案 | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D | A B C D |
1、已知集合
，
，则（ ）.
(A)
(B)P=Q (C)
(D)
2、
，
均为第二象限角，且
，则下列不等式成立的是（ ）.
(A)
(B) 
(C) 
(D) 
3、如右图，正方体ABCD–
中，EF是异面直线AC和
的公垂线，则EF和
的关系是（ ）.
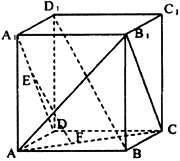
（A）相交不垂直 （B）相交垂直 （C）异面直线 （D）互相平行
4、设
，
，
，则有（ ）.
(A) a>b>c (B)a<b<c (C)a<c<b (D)b<c<a
5、设圆
与x轴交于A，B两点，则
的长为（ ）.
(A)
(B)
(C)
(D) 3
6、甲，乙，丙三个单位分别需要招聘工作人员2名、1名、1名，现从10名应聘人员中招聘4人到甲，乙，丙三个单位，那么不同的招聘方法共有（ ）.
(A) 1260种 (B)2025种 (C) 2520种 (D) 5040种
7、设
，
中
的系数为
，则
等于（ ）.
(A)
（B）
（C）
（D）2
8、直线
绕原点按顺时针方向旋转30°所得直线与圆
的位置关系是（ ）.
(A)直线与圆相切 (B) 直线与圆相交但不过圆心
(C)直线与圆相离 (D) 直线过圆心
9、若
时，不等式
恒成立，则a的取值范围是（ ）.
(A) (0,1) (B) (1,2) (C) 
(D) 
10、某产品的总成本y（万元）与产量x（台）之间的函数关系式是
，若每台产品的售价为25万元，则生产者不亏本时（销售收入不小于总成本）的最低产量是（ ）.
(A) 100台 (B) 120台 (C)150台 (D) 180台
11、已知方程
表示焦点y轴上的椭圆，则m的取值范围是（ ）.
(A) m<2
(B) 1<m<2 (C) m<–1或1<m<2 (D)m<–1或
12、对于已知直线a，如果直线b同时满足下列三个条件：（1）与a是异面直线；（2）与a所成的角为定值
；（3）与a的距离为定值d. 那样，这样的直线b有（ ）.
(A) 1条 (B) 2条 (C) 3条 (D) 无数条
二、填空题：本大题共4小题，每小题4分。共16分，把答案填在题中横线上。
13、已知
，则
的值是__________。
14、过抛物线
的焦点，且倾斜角为
的直线交抛物线于P、Q两点，O是坐标原点，则
的面积等于___________.
15、将一个圆形纸片沿其两个半径剪开，得到两个扇形，它们的圆心角之比为1∶2，再将它们当作圆锥侧面卷成两个圆锥，则这两个圆锥的体积之比是______________.
16、定义在
上的偶函数满足：
，且在
上是增函数，下面是关于的判断：
①是周期函数；
②的图象关于直线x=1对称；
③在
上是增函数；
④在上是减函数；
⑤
.
其中正确的判断是___________________(把你认为正确的判断都填上).
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
17、（本小题满分12分）
已知由正数组成的等比数列
，若前
项之和等于它前项中的偶数项之和的11倍，第3项与第4项之和为第2项与第4项之积的11倍，求数列的通项公式.
18、（本小题满分12分）
已知复数
，
的幅角主值分别为
，求
的最大值及对应的x的值.
19、（本小题满分13分）
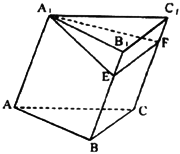
如图，已知三棱柱
的底面是边长为2的正三角形，侧棱
与AB，AC均成45°角，且
于E，
于F.
（I）
求证：平面
平面
；
（Ⅱ）求点A到平面的距离；
（Ⅲ）当
多长时，点
到平面ABC与平面的距离相等？
20、（本小题满分12分）
某乡为提高当地群众的生活水平，由政府投资兴建了甲、乙两个企业，1997年该乡从甲企业获得利润320万元，从乙企业获得利润720万元。以后每年上交的利润是：甲企业以1.5倍的速度递增，而乙企业则为上一年利润的
.根据测算，该乡从两个企业获得的利润达到2000万元可以解决温饱问题，达到8100万元可以达到小康水平。
（1）若以1997年为第一年，则该乡从上述两个企业获得利润最少的一年是那一年，该年还需要筹集多少万元才能解决温饱问题？
（2）试估算2005年底该乡能否达到小康水平？为什么？
21、（本小题满分12分）
椭圆中心是坐标原点O，集点在x轴上，
，过椭圆左焦点F的直线交椭圆于P，Q两点，
且
，求此椭圆的方程。
22、（本小题满分13分）
设是定义在
上的奇函数，
的图象与的图象关于直线
对称，而当
时，
（c为常数）
（1）求的表达式；
（2）对于任意
，
且
，求证：
.