北京市海淀区高三数学第二学期期中练习参考答案与评分标准(理科)
2001.5
一、选择题:
(1)C;(2)D;(3)A;(4)A;(5)C;(6)B;
(7)C;(8)C;(9)B;(10)C;(11)D;(12)D.
二、填空题:
(13)12;(14)![]() (15)x∈(0,2];(16)
(15)x∈(0,2];(16)![]() 中选一即可
中选一即可
三、解答题:
(17)解:(Ⅰ)设z=x + yi(x,y∈R)
依题意,![]()
∴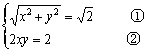 …………………………………………3分
…………………………………………3分
故![]()
∴![]()
∴x=±1,
∴![]()
∴z=1+i或z= –1–i………………………………………………5分
![]()
∴![]() ……………7分
……………7分
(Ⅱ)当z=1+i时,![]()
∴A(1,1)、B(0,2)、C(1,–1)
∴AC=2
![]() ………………………………………………10分
………………………………………………10分
当z=–1–i时,![]()
A(–1,–1)、B(0,2)、C(–1,–3)
则![]()
综上△ABC的面积为1.…………………………………………12分
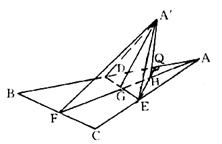
(18)解:(Ⅰ)∵△ABC是正三角形,AF是BC边的中线
∴AF⊥BC
又D、E分别是AB、AC的中点
∴BE![]()
![]()
|
∴![]()
![]() ⊥DE,GF⊥DE
⊥DE,GF⊥DE
∴DE⊥平面![]() …………………………4分
…………………………4分
又DE![]()
∴平面![]() ⊥平面BCED……………6分
⊥平面BCED……………6分
(Ⅱ)∵![]() ⊥DE,GF⊥DE
⊥DE,GF⊥DE
∴∠![]() 是二面角A′–DE–B的平面角……………………7分
是二面角A′–DE–B的平面角……………………7分
∵平面![]() ∩平面BCED=AF
∩平面BCED=AF
作![]() ⊥AG于H
⊥AG于H
∴![]() ⊥平面BCED………………………………………………9分
⊥平面BCED………………………………………………9分
假设![]() ⊥BD,连EH并延长交AD于Q
⊥BD,连EH并延长交AD于Q
∴EQ⊥AD……………………………………………………………10分
∵AG⊥DE
∴H是正三角形ADE的垂心,也是中心.
∵AD=DE=AE=![]()
∴![]()
在Rt△![]() 中,
中,![]()
∵∠![]() =π–∠
=π–∠![]() GH
GH
∴![]()
∴![]() 时…………………………………………11分
时…………………………………………11分
即当![]() ……………………………12分
……………………………12分
(19)解:(Ⅰ)∵当n≥2时,![]() 成等差数列
成等差数列
∴![]()
∴![]() ………………………………………………2分
………………………………………………2分
∴![]() ∵
∵![]() ,∴
,∴![]()
类似地![]() ∴
∴![]()
![]() ∴
∴ ![]() ……………………………4分
……………………………4分
(Ⅱ)∵当≥2时,![]() ,即
,即![]()
∴![]()
②–①,得![]()
∴![]() 为常数………………………………………………6分
为常数………………………………………………6分
∴![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…成等比数列.
,…成等比数列.
其中![]() ………………………………………………7分
………………………………………………7分
故![]()
∴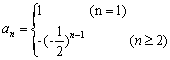 …………………………………………9分
…………………………………………9分
(Ⅲ)∵![]()
=![]()
∴![]()
=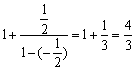 ………………………………12分
………………………………12分
(20)解:(Ⅰ)由已知数据,易知函数y=f(t)的周期T=12 ……………………1分
振幅A=3………………………………………………………………2分
b=10……………………………………………………………………3分
∴![]() ……………………………………………………4分
……………………………………………………4分
(Ⅱ)由题意,该船进出港时,水深应不小于5+6.5=11.5(米)
∴![]() …………………………………………………6分
…………………………………………………6分
∴![]()
解得,![]() …………………………8分
…………………………8分
![]()
在同一天内,取k=0或1
∴1≤t≤5或13≤t≤17………………………………………………10分
∴该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时
…………………………………………………………………………12分
(21)解:(Ⅰ)∵y=f(x)是以5为周期的周期函数
∴f(4)=f(4–5)=f(–1)……………………………………………1分
又y=f(x),(–1≤x≤1)是奇函数
∴f(1)= –f(–1)= –f(4)
∴f(1)+f(4)=0…………………………………………………3分
(Ⅱ)当x∈[1,4]时,由题意,可设
f(x)=![]() (a≠0)……………………………………………………5分
(a≠0)……………………………………………………5分
由f(1)+f(4)=0
得![]()
解得a=2
∴![]() (1≤x≤4)…………………………………………7分
(1≤x≤4)…………………………………………7分
(Ⅲ)∵y=f(x) (–1≤x≤1)是奇函数
∴f(0)= –f(–0) ∴f(0)=0………………………………………………8分
又y=f(x) (0≤x≤1 )是一次函数
∴可设f(x)=kx (0≤x≤1)
∵![]()
又f(1)=k·1=k
∴ k=–3
∴当0≤x≤1时 f(x)=–3x……………………………………………………9分
当–1≤x<0时,0<–x≤1
∴f(x)= –f(–x)= –3x
∴当–1≤x≤1时,f(x)=–3x………………………………………………11分
当4≤x≤6时,–1≤x–5≤1
∴f(x)=f(x–5)=–3(x–5)=–3x+15
当6<x≤9时 1<x–5≤4
![]()
![]()
∴f(x)=![]() …………………………………………12分
…………………………………………12分
|
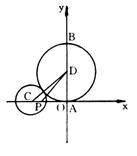
∴圆D半径r=5–2=3
此时,A、B坐标分别为(0,0)、(0,6)
PA在x轴上,BP斜率k=2
∴tg∠APB=2…………………………3分
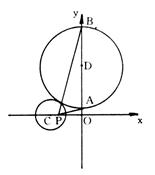
(Ⅱ)设D点坐标为(0,a),圆D半径为r,则![]()
A、B坐标分别为(0,a–r)、(0,a+r)设PA、PB斜率分别为![]() ,
,![]() ,则
,则
|
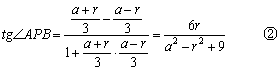
…………………………………………………6分
由①解出![]() 代入②,得
代入②,得![]() ,而8r–6为单调增函数,
,而8r–6为单调增函数,![]() .
.
∴![]()
∠APB的最大值为![]() ;……………………………………9分
;……………………………………9分
(Ⅲ)假设存在Q点,设Q(b,0),QA、QB斜率分别为![]() ,
,![]() ,则
,则![]()
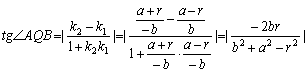 ……………………11分
……………………11分
将![]() 代入上式,得
代入上式,得
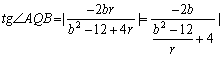
欲使∠AQB大小与r无关,当且仅当![]() ,即
,即![]() ,
,
此时![]()
∴存在Q点,当圆D变动时,∠AQB为定值![]() ,Q点坐标为(
,Q点坐标为(![]() )
)
…………………………………………………………………………………………14分
注:其他正确解法可按相应步骤给分