北京市海淀区高三数学第二学期期末练习参考答案与评分标准
2001.6
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | B | A | A | C | C | D | B | D | D | A |
二、填空题:
(13)![]() ;(14)
;(14)![]() ;(15)x = 0或15x + 8y – 32 = 0(写出一个方程给2分);(16)4.
;(15)x = 0或15x + 8y – 32 = 0(写出一个方程给2分);(16)4.
三、解答题:
(17)解:原不等式等价于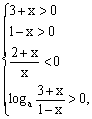 …………………………………………………3分
…………………………………………………3分
即
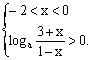
当a > 1时,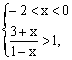
解得–1< x < 0;…………………………………………………………………………7分
当0 < a < 1时,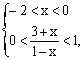
解得–2 < x <–1.………………………………………………………………………11分
所以当a > 1时原不等式的解集为![]() ;
;
当0 < a < 1时原不等式的解集为![]() .……………………………12分
.……………………………12分
(18)
(理科)
解:由已知得:![]()
∴![]() .……………………………………………………3分
.……………………………………………………3分
由正弦定理得a sinB = b sinA,
∴a cosA = b cosB.
又由正弦定理得2RsinA=a,2RsinB=b,
∴2RsinAcosA=2RsinBcosB,……………………………………………………………8分
即sin2A=sin2B
由已知A、B为三角形内角且A≠B,
∴2A+2B=180°.
即A+B=90°.
∴△ABC为直角三角形.……………………………………………………………12分
(文科)
解:(Ⅰ)由已知得![]() ,
,
∴b=1.……………………………………………………………………………3分
由余弦定理![]()
∴a=3.……………………………………………………………………………6分
(Ⅱ)由正弦定理得2RsinA=a,2RsinB=b,
∴2RsinAcosA=2RsinBcosB,……………………………………………………9分
即sin2A=sin2B.
由已知A、B为三角形内角,
∴A+B=90°或A=B,
∴△ABC为直角三角形或等腰三角形.………………………………………12分
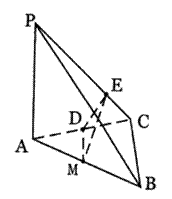 (19)
(19)
解:(Ⅰ)由已知PA⊥平面ABC,PA=AC=1,
∴△PAC为等腰直角三角形,且PC=CB=![]() ,
,
在Rt△PAB中∠PBA=30°,
∴PB=2,
∴△PCB为等腰直角三角形.
∵PA⊥平面ABC,PC⊥BC,
∴AC⊥BC,又![]() ,
,
∴BC⊥平面PAC,
∵![]() 平面PBC,
平面PBC,
∴平面PBC⊥平面PAC.…………………………………………………4分
(Ⅱ)三个侧面及底面都是直角三角形,求得侧面PAC面积值为![]() ,侧面PAB面积值为
,侧面PAB面积值为![]() ,侧面PCB面积值为1,底面积值为
,侧面PCB面积值为1,底面积值为![]() .
.
三个侧面面积的算术平均数为![]() .…………………………………7分
.…………………………………7分
∵![]() ,
,
其中![]() ,
,
∴三个侧面面积的算术平均数大于底面积的数值.……………………8分
(Ⅲ)如图,过M作MD⊥AC,垂足为D.
∵平面PAC⊥平面ABC且相交于AC,
∴MD⊥平面PAC.
过D作DE⊥PC,垂足为E,连结ME,则DE是ME在平面PBC上的射影,
∵DE⊥PC,∴ME⊥PC,ME的长度即是M到PC的距离.
在Rt△ABC中,MD∥BC,MD=![]() BC=
BC=![]() ,在等腰Rt△PAC中,DE=DCsin45°=
,在等腰Rt△PAC中,DE=DCsin45°=![]()
∴ME=![]() ,即点M到PC的距离为
,即点M到PC的距离为![]() .…12分
.…12分
(20)
解:(1)定义域为![]() ,……………………2分
,……………………2分
值域为![]() .……………4分
.……………4分
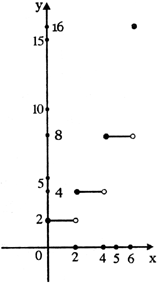
(2)如图:…………………………………8分
(3)n为偶数时:![]() ,……………10分
,……………10分
n为奇数时:![]() ,……………12分
,……………12分
(21)
解:(1)由已知得已知双曲线的离心率为![]() ,解得
,解得![]() ,所以已知双曲线方程为
,所以已知双曲线方程为![]() ,它的渐近线
,它的渐近线![]() 、
、![]() 的方程为
的方程为![]() .…………3分
.…………3分
(2)因为![]() ,所以AB=10.
,所以AB=10.
设A在![]() 上,B在
上,B在![]() 上,则可以设A
上,则可以设A![]() 、B
、B![]() ,
,
∴![]() ①…………………………………………5分
①…………………………………………5分
设:AB的中点M(x,y),则![]() .
.
∴![]() ,………………………………………………9分
,………………………………………………9分
代入①得![]() ,
,
即![]() 为中点M的轨迹过程,
为中点M的轨迹过程,
轨迹为椭圆.…………………………………………………………………12分
(22)
解:原函数可化为:![]() ……………………………………………………2分
……………………………………………………2分
(Ⅰ) y = 1时,可求得![]() ,即
,即![]() ,
,
∴![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
∴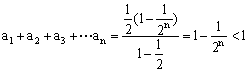 .………………………………7分
.………………………………7分
(Ⅱ)同理可以求![]() 、
、![]() 的横坐标,可得
的横坐标,可得![]() 、
、![]() 的坐标分别为
的坐标分别为![]() .因此
.因此![]() .
.
因此![]()
![]() 中点C到y轴距离
中点C到y轴距离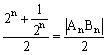 ,
,
∴以C为圆点、![]()
![]() 为直径的圆必与定直线y轴相切,这条定直线的方程为x=0.由点C的纵坐标为0,可知从点C到y轴作垂线的垂足就是原点即切点,所以切点坐标为(0,0).………………………………………………………………………………………14分
为直径的圆必与定直线y轴相切,这条定直线的方程为x=0.由点C的纵坐标为0,可知从点C到y轴作垂线的垂足就是原点即切点,所以切点坐标为(0,0).………………………………………………………………………………………14分
(说明:囿于篇幅,本答案只给出一种解法,其他解法可相应给分.)