63.球
一、典型例题
1. 把地球看作半径为R的球,A、B是北纬a度圈上的两点,它们的经度差为b,求A、B两点间的球面距离。[2Rarcsin(xosa·sinb/2)]
2. 圆锥和一个球面相交,球心是圆锥的顶点,半径等于圆锥的高,若圆锥的侧面积被球与圆锥侧面的交线所平分,求圆锥母线与底面所成角的大小。[45°]
3.
过半径为R的球面上一点作三条两两垂直的弦MA、MB、MC,①求证:MA2+MB2+MC2为定值;②求三棱锥M-ABC体积的最大值。[4R2、![]() ]
]
4.
已知球的半径为R,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?[![]() ]
]
5.
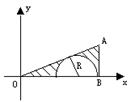 如图,A为直线y=
如图,A为直线y=![]() x上一点,AB⊥x轴于B,半圆的圆心
x上一点,AB⊥x轴于B,半圆的圆心![]() 在x轴的正半轴上,且半圆与AB、AO相切,已知⊿ABO绕x轴旋转一周形成的几何体的体积为
在x轴的正半轴上,且半圆与AB、AO相切,已知⊿ABO绕x轴旋转一周形成的几何体的体积为![]() ,求阴影部分旋转成的几何体积和表面积。[5
,求阴影部分旋转成的几何体积和表面积。[5![]() 、39p]
、39p]
6.
已知一个圆锥和一个圆柱的底面在同一个平面内,且有一个公共的内切球,①求证:它们的体积不可能相等;②若V锥=kV柱,求k的取值范围。[![]() ]
]
7. 正四面体的内切球和外接球的半径分别是r和R,求r∶R。[1∶3]
8. 如果球、正方体与等边圆柱的体积相等,求它们的表面积S球、S正方体、S柱的大小关系。[S球< S柱< S正方体]