高三数学综合训练(7)
1．选择题
(1)已知
,x是第二象限角,那么tgx的值等于
A 5/12 B 12/5 C –5/12 D -12/5
(2)在等差数列{an}中,a1+a4+a7=39,a2+a5+a8=33,则a3+a6+a9等于
A 30 B 27 C 24 D 21
(3)长方体共顶点的三条棱的长分别为3,4,5,且它的八个顶点都在一个球面上,则这个球的表面积是
A
B 
C 
D 
(4)已知全集I=R,集合A为函数
的定义域,集合B={x
},则
为
A
(1,2)
B 
C
D 
(5)已知定直线l:f (x,y)=0及其外一点P (x0,y0),则方程f (x,y)- f (x0,y0)=0表示的直线
A 过P且与l斜交 B 过P且与l垂直 C 过P且与l平行 D 可能不过P
(6)(理)极坐标方程4sin2θ表示的曲线是
A 双曲线 B 两条相交直线 C 圆 D 两条射线
(文)方程
表示的图形是
A 双曲线的一部分 B 圆的一部分 C 两个圆 D 椭圆的一部分
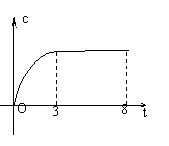(7)某工厂8年来某种产品的总产量c与时间t (年)的函数关系如右图,下列四种说法:①前三年,产量增长的速度越来越快; ②前三年中,产量增长的速度越来越慢; ③第三年后,这种产品停止生产; ④第三年后,年产量保持不变.其中说法正确的是:
A ②,③ B ②,④ C ①,③ D ①,④
(8)(理)已知arctgx=arccos(-1/3),则x的值为
A
B 
C 
D 以上都不对
(文)下列不等式中成立的一个是
A ctg3>ctg4 B tg3>tg4 C cos3>cos4 D sin3>sin4
(9)圆锥底面半径为
,高为1,过顶点的截面面积的最大值是
A
B 2
C 
D 4
(10)已知z≤1,则arg (z-2i)的最大值是
A 2π/3 B 4π/3 C 5π/3 D 11π/6
(11)在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O是底面AC的中心,P为棱A1B1上任意一点,则直线OP与AM所成的角等于
A 90° B 60° C 45° D 30°
(12)椭圆x2/a2+y2/b2=1
(a>b>0)的半焦距是c,A,B分别是长轴、短轴的一个端点,若△AOB(O是原点)的面积是
,则此椭圆的离心率是
A
B 
C 1/2
D 
(13)5个身高均不相同的学生站成一排合影,高个子站中间,从中间到两边一个比一个矮,则这样的排法共有
A 4种 B 6种 C 8种 D 16种
(14)如果函数y=sin2x+acos2x的图像关于直线x=-π/8,那么a等于
A
B 
C 1
D -1
(15)函数y=f (x) 在(0,2)上是减函数,且关于x的函数y=f (x+2)是偶函数,那么有
A f (1/2)<f (5/2)<f (3) B f (3)<f (5/2)<f (1/2) C f (3)<f (1/2)<f (5/2) D f (5/2)<f (3)<f (1/2)
2.填空题
(16)函数y=sinπx/2sinπ(x-1)/2的最小正周期是
(17)(4x3-3x2+1)8的展开式中x2的系数是 (用数字作答)
(18)若抛物线y2-mx-2y+4m+1=0的准线与椭圆x2/25+y2/9=1的右准线重合,则m的值是
(19)关于三直线a,b,c和三平面α、β、γ有下列命题:
①α∥β,β∥γ,则α∥β; ②a⊥γ,b⊥γ,则a∥b; ③a⊥γ,β⊥γ,则a∥β;
④a⊥c,b⊥c,且a,b共面,则a∥b; ⑤a∥α, a⊥β,则α⊥β.
其中正确的命题的序号是 .(注:把你认为正确的命题序号都填上.)
3.解答题
(20)在△ABC中,其周长为10,且BC=4,求tgB/2tgC/2之值.
(21)数列{an}对一切自然数n满足 a1+a2/ r+a3/ r2+…+ an/ rn-1=9-bn,其中r为常数,且r>1.
( I )求数列{an}的通项公式; (II)若bn =an· sin nπ/2, Sn =b1+b2+b3+…+ bn-3求
.
(22)三棱台ABC-A1B1C1中A1B1是A1C与B1C1的公垂线,已知AB=3 A1B1=2,A1A=AC=5,二面角A1-AB-C为60°.
(I) 求证:平面A1BC⊥平面ABC; (II)求二面角A1-AC-B的正切值;(III)求三棱台ABC-A1B1C1的体积.
(23)从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形(如图),再将四边向上折起,做成一个无盖的长方形铁盒,要求长方体的高度x与底面正方形边长的比不超过常数t.
(I)把铁盒的容积V表示为x的函数,并指出其定义域; (II)x取何值时,容积V有最大值?
(24)已知双曲线C1:2x2-y2=2m2(m>0),抛物线C2的顶点在原点,焦点F与C1的左焦点重合.
(I)求证:C1与C2总有两个不同的交点;
(II) (理)直线l过点F且与C2相交于A,B,试问:是否存在使△OAB的面积为6的直线l?如果存在,求出m的取值范围;如果不存在,说明理由.
(文)直线l过点F且与C2相交于A,B,当m=1, △OAB的面积为12时,求直线l的方程.
(25)(理)已知奇函数f (x)在
上有意义,且在
上是减函数, f (3)=0,又有
,若
,集合
，求
.
(文)已知奇函数在上是增函数,是否存在这样的实数m,使
对所有的
均成立?若存在,则求出所有适合条件的实数m;若不存在,说明理由.