福州市高三数学质量检测试题答案
一、1.C 2.D 3.C 4.A 5.C 6.C 7.C 8.B 9.C 10.D 11.B 12.A
二、13.![]() 14.420 15.2
14.420 15.2![]() 16.
16. ![]()
三、17.解:(理)∵![]()
∴cos(-α)+isin(-α)+cos(-β)+isin(-β)= ![]() -
-![]() i 2分
i 2分
∴(cosα+cosβ)-(sinα+sinβ)i=![]() -
- ![]() i
i
![]() ∴ cosα+cosβ=
∴ cosα+cosβ=![]() ①
①
sinα+sinβ=![]() ② 4分
② 4分
①2+②2得:2+2cos(α-β)= ![]() 即cos(α-β)=-
即cos(α-β)=-![]() 6分
6分
由①得:2cos![]() cos
cos![]() =
=![]() ③
③
由②得:2sin![]() cos
cos![]() =
=![]() ④ 8分
④ 8分
④÷③得:tg![]() =
=![]() 10分
10分
∴cos(α+β)= 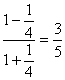 12分
12分
(文)(Ⅰ)由y=2x+a 2x=y-a x=log2(y-a) 2分
∴f-1(x)=log2(x-a) 4分
定义域为{xx>a} 5分
(Ⅱ)由已知得1=log2(x+a-a)且2=log2(x-2a)
![]() 即 log2x=1
即 log2x=1
log2(x-2a)=2 7分
即![]() 9分
9分
∴P(1,1)、Q(3,2).则PQ的中点R坐标是(2,![]() ) 12分
) 12分
18.证明:(Ⅰ)取PD中点Q,连EQ、AQ,则∵QE∥CD,CD∥AB,∴QE∥AB,
又QE=![]() CD=AB
CD=AB
∴ABEQ是平行四边形,∴BE∥AQ
又AQ![]() 平面PAD
平面PAD
∴BE∥平面PAD 3分
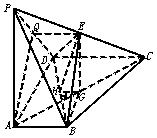 (Ⅱ)∵PA⊥底面ABCD ∴CD⊥PA,又CD⊥AD
(Ⅱ)∵PA⊥底面ABCD ∴CD⊥PA,又CD⊥AD
∴CD⊥平面PAD ∴AQ⊥CD
若PA=AD,∵Q为PD中点
∴AQ⊥PD
∴AQ⊥平面PCD
∵BE∥AQ,∴BE⊥平面PCD 7分
(Ⅲ)连结AC,取AC的中点G,连EG,EG∥PA
∵PA⊥平面ABCD,∴EG⊥平面ABCD
过G作GH⊥BD,连EH,则EH⊥BD
∴∠EHG是二面角E—BD—C的平面角 10分
设AB=1,则PA=AD=DC=2AB=2.
∴EG=![]() PA=1,DB=
PA=1,DB=![]() ,
,
又∵∠CAB=∠ACD, ![]() ,
,
∴△ACD∽△ABG,∴BG=![]() AD=1,∠ABG=∠ADC=90°,
AD=1,∠ABG=∠ADC=90°,
∴BG∥AD,∠GBH=∠ADB,∴△ABD∽△HBG.
∴![]()
∴HG=![]()
∴tgEHG=![]() . 12分
. 12分
19.解:(Ⅰ)∵Sn=![]() (n2-n+2) ∴a1=S1=1;
(n2-n+2) ∴a1=S1=1;
当n≥2时,
an=Sn-Sn-1=![]() (n2-n+2)-
(n2-n+2)- ![]() [(n-1)2-(n-1)+2]=n-1
[(n-1)2-(n-1)+2]=n-1
∴an=![]() 3分
3分
又b1=1且bn-bn-1=![]() (n≥2)
(n≥2)
∴bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1) 5分
=1+![]() +
+![]() 7分
7分
(Ⅱ)(i)当n=1时,∵a1=1,b1=1 ∴a1>5b1不成立;
(ii)当n≥2时,若an>5bn恒成立
即n-1>5(2-![]() )恒成立
)恒成立
只须n>11-![]() 恒成立 11分
恒成立 11分
由于n≥2时,11-![]() <11
<11
∴令n0=11,则当n≥11时,恒有an>5bn 12分
20.解:(Ⅰ)q=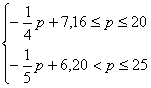 3分
3分
(Ⅱ)设月利润为W(万元),则
W=(p-16)q-6.8=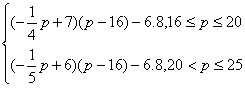 5分
5分
当16≤p≤20,W=-![]() (p-22)2+2.2
(p-22)2+2.2
当p=20时,Wmax=1.2 7分
当20<p≤25,W=-![]() (p-23)2+3
(p-23)2+3
当p=23时,Wmax=3
∴当售价定为23元/件时,月利润最多为3万元 9分
(Ⅲ)设最早n个月后还清转让费,则
3n≥58,n≥20,∴企业乙最早可望20个月后还清转让费 12分
21.解:(Ⅰ)设A(![]() ,y1),B(
,y1),B(![]() ,y2) 1分
,y2) 1分
∵∠AQP=∠BQP
∴tgAQP=tgBQP
∴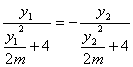 3分
3分
∴y1y2(y1+y2)=-8m(y1+y2)
∵l不垂直于x轴,∴y1+y2≠0
∴y1y2=-8m 4分
∵O点是PQ的中点,且Q(-4,0),∴P(4,0)
又kAP=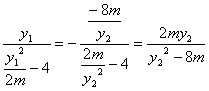
kAP=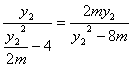 6分
6分
∴kAP=kBP
∵AP与BP都过P点 ∴A、P、B三点共线 8分
(Ⅱ)假设l′存在,设其方程为x=n
设A(x1,y1)则y12=4x1
∵以AP为直径的圆的圆心C(![]() )
)
∴直线l′被圆截得的弦长为
![]() 10分
10分
![]()
∴当n=3时,弦长为定值2![]()
∴存在直线l′:x=3满足要求 12分
22.解:(Ⅰ)f(x)的反函数是f-1(x)=log2(x-a)(x>a)
∵P、Q、R是f-1(x) 图象上不同三点
∴y1=log2x,y2=log2(x-a),y3=1 2分
∵是不同三点,∴a≠0(即x≠2) 3分
已知y1、y2、y3成等差数列,即y1+y3=2y2
∴1+log2x=2log2(x-a),即log2![]() =log2(x-a)
=log2(x-a)
x-a=![]() x>0且x>a
x>0且x>a
∴a=x-![]() (x>0且x≠2) ① 5分
(x>0且x≠2) ① 5分
|
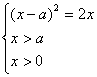 又等价于
又等价于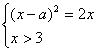
方程②等价于x2-2(a+1)x+a2=0 ④
Δ=[2(a+1)]2-4a2=8a+4 8分
1°当a=-![]() 时,Δ=0,方程④仅有一个实数解x=
时,Δ=0,方程④仅有一个实数解x=![]() 且满足③
且满足③
∴a=-![]() 满足①有惟一解
满足①有惟一解
2°当a>-![]() 时,Δ>0,方程②有二个相异实数解
时,Δ>0,方程②有二个相异实数解
x1=a+1+![]() ,x2=a+1-
,x2=a+1-![]()
又x1=a+1+![]() >a ∴x1>a满足条件③
>a ∴x1>a满足条件③
∴x1是方程①的解 11分
要使方程①有惟一解,则x2不能是①的解
∴x2=a+1-![]() ≤a
≤a
![]() ≥1,
≥1, 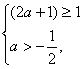 a≥0.
a≥0.
∵a≠0
∴a>0 综合1°,2°,a的取值范围是a=-![]() 或a>0 14分
或a>0 14分