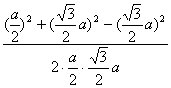数学文科:模拟试卷八
一、选择题：
1. 满足关系{1}真包含于M,且M真包含于{1,2,3,4}的集合M有（ ）
（Ａ） 5个 （Ｂ） 6个
（Ｃ） 7个 （Ｄ） 8个
2. 函数
(x∈R)的值域是（ ）
（Ａ） (0，1] （Ｂ） (0,+∞)
（Ｃ） (1,+∞) （Ｄ） [1,+∞)
3. 若a ＜ 0, b＞0且a
＞b，则下列不等式正确的是（ ）
（Ａ） a＞-b＞b＞-a （Ｂ） -a＞b＞-b＞a
（Ｃ） b＞-a＞a＞-b （Ｄ） -b＞a＞-a＞b
4. 过点M(2，1)的直线l与x轴、y轴分别相交于P、Q两点，且｜MP｜=｜MQ｜
则直线l的方程是（ ）
（Ａ） x-2y+3=0 （Ｂ） 2x-y-3=0
（Ｃ） 2x+y-5=0 （Ｄ） x+2y-4=0
5. 一梯子共有11条横档，相邻两档间的距离都相等，已知最下一档长为50cm，
最上一档长为40cm，则从下到第7档的横档长为（ ）
（Ａ） 43cm （Ｂ） 44cm
（Ｃ） 45cm （Ｄ） 46cm
6. 给出命题：
(1)异面直线是指空间两条既不平行又不相交的直线
(2)两条异面直线a,b，如果a∥平面α,那么b不平行平面α
(3)两条异面直线a,b,如果a⊥平面α，那么b不垂直平面α
(4)两条异面直线在同一平面内射影不可能是两条平行线。
对于以上四个命题,以下判断中正确的是（ ）
（Ａ） (1)(3)对，(2)(4)错 （Ｂ） (1)(2)对，(3)(4)错
（Ｃ） (2)(3)对，(1)(4)错 （Ｄ） (3)(4)对，(1)(2)错
7. 设等比数列
,(q＞1,n∈N)的前n项和为Sn，则 
（ ）
（Ａ） 0 （Ｂ） 1
（Ｃ） q
（Ｄ） q
8. 已知cos(α+β)+cos(α-β)=a,cos(α+β)-cos(α-β)=b
则(1-cos4α)(1-cos4β)的值为（ ）
（Ａ）a-b
（Ｂ） -2ab
（Ｃ）4ab
（Ｄ） 
9. 若复数z满足｜z+1｜-｜z-i｜=1，则z在复平面内表示的图形是（ ）
（Ａ） 圆 （Ｂ） 椭圆
（Ｃ） 双曲线 （Ｄ） 直线
10. 抛物线y=
关于直线x-y=0对称的抛物线的焦点坐标是（ ）
（Ａ）(1，0) （Ｂ）(0，1)
（Ｃ）(0，
)
（Ｄ）(,0)
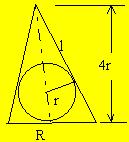
11. 如果一个球的外切圆锥的高是这个球的直径的2倍，那么这个圆锥的全面积
与球面积的比为（ ）
（Ａ） 2:1 （Ｂ） 4:1
（Ｃ） 2:3 （Ｄ） 4:3
12. 已知
P(x,y) 是函数 y=32x
的图象在第一象限上的一点，则 x+y 的
最小值是（ ）
（Ａ） 3 （Ｂ） 4
（Ｃ） 5 （Ｄ） 6
13. 自然数n，是方程x-1997x+64=0两根的等比中项，那么
展开式中x
的系数是（ ）
（Ａ） 14 （Ｂ） -14
（Ｃ） 56 （Ｄ） -56
14. 已知P是椭圆
上的一点，F1、F2是该椭圆的两个焦点，且∠F1PF2=90°，
则△F1PF2的面积是（ ）
（Ａ） 
（Ｂ）
（Ｃ） 1 （Ｄ） 4
15. 已知不等式x-2ax+a＞0对于任意实数x恒成立，则不等
式
＜
＜1的解集为（ ）
（Ａ） (1，2)
（Ｂ） (
,2)
（Ｃ） (-2,2) （Ｄ） (-3,2)
二、填空题：
16. 方程：
·
=2的解是（ ）
[分析解答]
17. 有四个不同的红球，六个不同的白球，假设取出一个红球记2分，取出一个白
球记1分，如果每次取4个球，使总分不少于5分，这样的取法有（ ）。
[分析解答]
18. 设复数ω适合｜ω｜=1,复数z适合 z+
=6 ，则｜ω-z｜的最小值是( $W*2$ )
[分析解答]
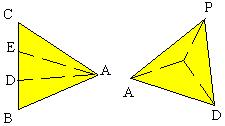
19. 如图已知△ABC为等边三角形，边长为a，D、E是BC边上的两个三等分点，沿AE、
| AD折起，使B、C点重合为一点P，那么P点到平面ADE的距离是( )。
（Ａ）  （Ｂ） （Ｃ） |
（Ｄ）
[分析解答]
三、解答题
20. 已知复数z满足｜z｜-z=
，若u=z，求复数 u 的代数形式。( )
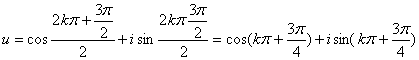(k=0,1)
[分析解答]
21. 已知
求tgx的值( $W*1$ )。
[分析解答]
|
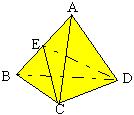
22. 正四面体A—BCD中的棱长为a，E是AB的中点。 (1) 求证平面ABC⊥平面CED。 |
[分析解答]
(2) 求异面直线DE与BC所成的角的余弦值( )。
（Ａ）
（Ｂ）
。
（Ｃ）
（Ｄ）
。
[分析解答]
23. 已知函数 
(1+x)(a＞0且a≠1)对于任意x1＞0,x2＞0，试判断
与 
的大小关系( )。
（Ａ）＞
（Ｂ）≤
（Ｃ）＜
（Ｄ）≥
[分析解答]
24. 已知数列 {an}
的前n项和为Sn 且 
(n∈N)
(1) 判断数列 {an} 是怎样的数列，并说明理由。
[分析解答]
(2) 试用 n 表示Sn。
[分析解答]
25. 设抛物线 C 的准线方程为
，点(6，2)在其对称轴上，且直线l:y=x-1
被抛物线 C 截得的弦长为 
，求抛物线 C 的方程( )。
（Ａ）(y-2)=x+1
（Ｂ）(y-4) =x-1
（Ｃ）(y-2) =x-1
（Ｄ）(y+2) =x-1
[分析解答]
参 考 答 案
一、
1. B
[分析解答] 由{1}＜M＜{1,2,3,4}知，集合M是集合{1}的真子集，又是集合{1,2, 3,4}的真子集，而集合{1,2,3,4}比集合{1}多3个元素，于是符合要求的集合M的个数是 2
-1-1=6个。
2. D
[分析解答]
｜x+1｜ ≥ 0
3. B
[分析解答] a＜0, b＞0, a＞b
(-a) ＞b
=> -a＞b
-a＞0, b＞0
∴ => ∴-a＞b＞-b＞a。
b＞0, ∴ b＞-b
-a＞b, -b＞a
4. D
[分析解答]
设所求直线方程为
a=4
b=2
∴
∴x+2y-4=0
5. B
[分析解答]
a1=50,a11=40 ∴ 40=50+10d d=-1
所求a7=50+(7-1)×(-1)=44
6. A
7. D
[分析解答] q＞1, ∴ 
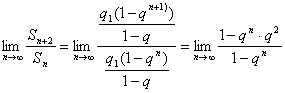
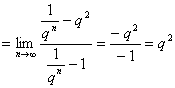
8. C
[分析解答]
cos(α+β)+cos(α-β)=a
∴2cosαcosβ=a cos(α+β)-cos(α-β)=b ∴-2sinαsinβ=b
(1-cos4α)(1-cos4β) = 2sin2α·2sin2β
= 4(2cosαcosβ) (2sinαsinβ) = 4a(-b) = 4ab
9. D
[分析解答]
设z=x+yi,｜z+1｜-｜z-i｜=1
∴(x+1) +y-x-(y-1) =1
∴x+2x+1+y-x-y+2y-1=1
∴2x+2y-1=0表示直线。
10. C
[分析解答]
y=
x关于x-y=0对称，得x=
,
∴ 
该抛物线
的焦点为(0，)
11. A
[分析解答]
|
 9R |
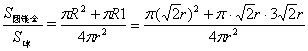
12. D
[分析解答]
y=32x,(x,y) 点在第一象限，∴x＞0,y＞0,xy=32
≥
又解：
(x,y＞0)
≥ 
13. B
[分析解答] x1x2=64,n=±
=±8,n∈N, n=8
, 
∴16-3r=7 3r=9 r=3
x系数为(-1)·2
14. C
[分析解答]
∠F1PF2=90°，设P点的两条焦点半径为r1,r2,
那么(2c) =
+
=(r1+r2) -2r1r2
r1+r2=2a=2×2=4. 
∴ 
r1r2=
S△F1PF2=
r1r2=·2=1
15. A
[分析解答]
x-2ax+a＞0,x∈R
∴△=4a-4a＜0 a(a-1)＜0 0＜a＜1
a
＜a
＜1
2x+1＞0 x＞
x+2x-3＞0 (x+3)(x-1)＞0,x＜-3或x＞1
2x+1＞x+2x-3 x＜4, -2＜x＜2
x＞
x＜-3或x＞1 1＜x＜2 -2＜x＜2
二、
16. ( x=0 )
[分析解答]
2
+1=2 2=1 x=0
17. ( 195 )
[分析解答]
取四个球，不能同时取4个全是白球，此时总分为4分而小于5分，所以
18. ( 2 )
[分析解答]
|
｜ω｜=1,ω对应点为单位圆 又z=x+yi 那么 z+ ∴ z=3+yi z对应的点为(3，0)点且与x轴垂直的直线。 显然｜ω-z｜最小值是z与ω的最短距离是2。 |
19. D
[分析解答] 
取DE中点O，连AO、PO。
正△ABC中，
,
PA=AB=AC=a,
正△PDE中，
△POA中：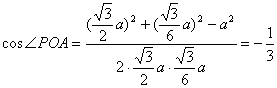
作PH⊥AO,∴PH为P点到平面ADE的距离
三、
20. 对
[分析解答] ｜z｜-z=
设z=x+yi ∴ 
y=-1代入上式
-y=1
x+1=1+2x+x x=0
x=0
∴z=-i
y=-1
u=z ∴u=-i u=cos
+isin
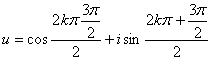
,(k=0,1)
21. 1
[分析解答]
, tgx+sin2x=2+2cos2x
tgx+tgx+2tgx=2+2tgx+2-2tgx
∴tgx+3tgx-4=0
tgx-tgx+tgx-tgx+4tgx-4=0
(tgx-1)(tgx+tgx+4)=0
tgx+tgx+4恒大于零
∴tgx-1=0
tgx=1
22.(1)
[分析解答] 证：
正四面体A—BCD中，△ABC，△ABD为正三角形。
E为AB中点，∴AB⊥CE,AB⊥DE ∴AB⊥平面CED
∵AB在平面ABC内， ∴平面ABC⊥平面CED。
(2) B
[分析解答] 作EF∥BC,E是AB中点，EF=
，
|
连结DF，正△DAC中，  ,同样 △DEF中，cos∠DEF= |
∴异面直线DE、BC成角∠DEF的余弦值为。
23. D
[分析解答] (1+x)(a＞0且a≠1)
x1,x2∈(0,+∞) ∴
≤ 
∴a＞1时
≤ 
≤
0 ＜ a ＜ 1时 ≥
≥
24. (1)
[分析解答]
3an=-2an+2an-1 ∴5an=2an-1
又S1=a1 ∴ a1=1-
, 
{an} 是首项为 
，公比为 
的等比数列。
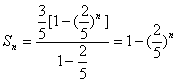
(2)
[分析解答]
Sn=1-
an,an=Sn-Sn-1 ∴Sn=1-(Sn-Sn-1)
3Sn=3-2Sn+2Sn-1 5Sn-2Sn-1=3
由 得 
数列
}为首项
,公比为的等比数列。
数列
的前n-1项的和为
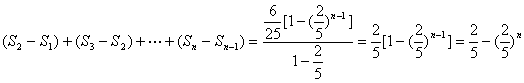
即
由
即得 
(n ≥ 2)
∴ 
(N∈N) ∴{an}为首项 ,公比为 的等比数列。
25. C
[分析解答]
所求抛物线准线为
, 点(6，2)在对称轴上 ∴抛物线的对称轴为y=2
又抛物线被直线y=x-1所截 ∴抛物线必开口向右设抛物线顶点为(xO,2)，
且xO＞
∴ 
抛物线方程为
(y-2) =(4x0-3)(x-x0) y=x-1
∴(x-3) =(4x0-3)(x-x0) x-6x+9=4x0x-3x-
+3x0
∴x-(3+4x0)x+-3x0+9=0 被直线所截得的弦长为,
得
9+24x0+
-+12x0-36=9
36x0-36=0
x0=1 所求抛物线方程为：(y-2) =x-1