上学期高三第二次月考-数学（理）

耀华中学2005届高三第二次月考

数学试卷（理科）

一、选择题：（每小题5分，共60分）

1. 集合　x│0＜│x-1│＜4，xN的真子集的个数为（　　）

A. 32　　  B. 31　　　 C. 16　　  D.　15

2. 复数的值为（　　  ）

　　A. –2i　　 B.　0　　　 C.　2i　　　D.　-i

3. 已知集合A=（x，y）│x+y=1　 ，映射：f∶A→B，在f 作用下，点（x，y）的象为（2^x，2^y），则集合B为（　　　　 ）

　A.（x，y）│x+y=2，x＞0，y＞0　　　　B. （x，y）│x·y=1，x＞0，y＞0　　　　

　　C. （x，y）│x·y=2，x＜0 ，y＜0　　  D. （x，y）│x·y=2，x＞0，y＞0

4. 采用简单随机抽样从含有6个个体的总体中抽取一个容量为3的样本，个体a前两次未被抽到，第3次被抽到的概率为（　　）

　　A. 　　　　　 B. 　　　　　　 C. 　　　　 D.

5. 已知f（x）=x²+2x·f＇（1），则f＇（0）等于（　　  ）

　 A. 0　　　　　　　 B. –4　　　　  C. –2　　　　　  D. 2

6. 函数f（x），g（x）在区间[a，b]上恒有：g（x）＞0及f＇(x)·g（x）＞g（x）·g＇(x)，则对任意x（a，b）都有（　　　）

　　A. f（x）·g（x）＞f（a）·g（a）　 B. f（x）·g（x）＞f（b）·g（b）

　  C. f（x）·g（a）＞f（a）·g（x）　 D. f（x）·g（b）＞f（b）·g（x）

7. 数列{a_n}是公差不为零的等差数列，并且a₅，a₈，a₁₃是等比数列{b_n}相邻三项，若b₂=5，则b_n等于（　　 ）

　　A. 5·　　B. 3·　　　 C. 3·　　D. 5·

8. 已知a＞0，a≠1，函数y=a│x²-x-2│的图象与函数y=│log_ax│的图像的交点个数是（　 ）

　　A. 1个　　　B. 2个　　　　  C. 3个　　　　  D. 4个

9. 已知f（x）=log₃x+2，x[1，3]，则函数F（x）=[f（x）]²+f（x²）的最大值为（　　）

　　A. 13　　　　B. 16　　　　　 C. 18　　　　　 D.  

10.数列1，2，2，3，3，3，4，4，4，4，5，5，5，5，5，6，……的第1000项的值是（　　）

　　A. 42　　　 B. 44　　　　　  C. 45　　　　  D. 51

11. 某商场对顾客实行购物优惠活动，规定一次购物：

①如不超过200元，则不予优惠；

②如超过200元，但不超过500元，按9折优惠；

③如超过500元，其中500元的按9折给予优惠，超过500元的部分按8折给予优惠，

某人两次去购物，分别付款168元和423元，若他只去一次购买同样价值的商品，则应付款（　　 ）

A. 472.8　　　B. 510.4　　　　　 C. 522.8　　　  D. 560.4

12. 在任意两个正整数m，n间定义某种运算（用×表示运算符号），当m，n都为正偶数或都为正奇数时，m×n=m+n，如4×6=4+6=10，3×7=3+7=10，当m，n中一个为正奇数，另一个为偶数时，m×n=mn，如3×4=34=10，4×3=43=12则上述定义下，集合

M=（a，b）│a×b=36，a，bN*　中元素个数为（　　　）

　　A. 24　　B.　35　　C.　41　  D. 23

二、填空题：（每小题4分，共16分）

13. 函数f（x）=log（x²-5x+6）的单调递增区间为_________________.

14. 一个盒子装有8个红球和2个白球，从中每次取出一个球，取后放回，共取两次，若取出红球的次数为ξ，且η=2ξ+1，则Eη=_____________Dη=_____________.

15. 在数列{a_n}中，a_n+s_n=n（n≥1），其中s_n=a₁+a₂+…a_n， 则a_n=_________________.

=_______________.

16. 设数集M= x│m≤x≤m+　　，N==x│n-≤x≤n，且M，N都有是集合

x│0≤x≤1　 的子集，如果把b-a叫做集合x│a≤x≤b　的“长度”，那么集合M∩N的“长度”的最小值是________________.

三、解答题：（共74分）

17. （本题12分）一批零件有5个合格品及2个次品，安装机器后，从这批零件中任意取出1个，如果每次取出的次品不再放回去，已知取得合格品之前已取出的次品率为ξ，

求（Ⅰ）ξ的概率分布列；

（Ⅱ）Eξ。

18.（本题12分）定义在R上的单调函数f（x）满足f（3）=log₂3，且对任意x，yR都有f（x+y）=f（x）+f（y）,

（1）求证f（x）为奇函数；

（2）若f（k·3^x）+f （3^x-9^x-2）＜0对任意xR恒成立，求实数k的取值范围。

19. （本题12分）这是一个计算机程序的操作说明：

①初始值x=1，y=1，z=0，n=0；

②n=n+1（将当前n+1的值赋予新的n）

③x=x+2（将当前x+2的值赋予新的x）

④y=2y（将当前2y的值赋予新的y）

⑤z=z+xy（将当前z+xy的值赋予新的z）

⑥如果z＞7000则执行语句⑦，否则回到语句②继续进行：

⑦打印n，z;

⑧程序终止。

由语句⑦打印出的数值为_____________、_______________

并写出计算过程。

20.（本题12分）已知≤a≤1，若函数f（x）=ax²-2x+1在区间[1，3]上的最大值为M（a），最小值为N（a），令g（a）=M（a）-N（a）

（Ⅰ）求g（a）的函数表达式；

（Ⅱ）判断函数g（a）在区间[，1]上的单调性，并求出g（a）的最小值。

21. （本题12分）已知f（x）=，（x≠-，a＞0），f（1）=log₁₆2，f（-2）=1,

（Ⅰ）求f（x）得表达式；

（Ⅱ）若数列{x_n}满足x_n=[1-f（1）]·[1-f（2）]…[1-f（n）]，试求x₁，x₂，x₃，x₄的值，并由此猜想出x_n的表达式，并证明你的结论。

22. （本题14分）已知f（x）=x³+bx²+cx+d在（-，0）上是增函数，在[0，2]上是减函数，且方程f（x）=0有三个根，它们分别为α，2，β。

（Ⅰ）求c的值；

（Ⅱ）求证f（1）≥2;

（Ⅲ）求│α-β│的取值范围。

耀华中学2005届高三第二次月考数学试卷（文科）参考答案：

一、选择题：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	A	D	C	B	C	B	C	D	C	D	C

二、填空题：13.（-，2）。　14. Eη=21/5 ；Dη=32/25。 15　a_n=1-；　16. 1/12。

三、解答题：17. （Ⅰ）　　　　　　　　　　 （Ⅱ）Eξ=

ξ	0	1	2
P	5/7	5/21	1/21

18. （Ⅰ）令x=y=0，得f（0）=0；令y= -x，则f（x-x）=f（x）+f（-x）=f（0）=0，

得函数f（x）为奇函数；（Ⅱ）单调函数f（x）满足f（3）=log₂3＞0 = f（0），函数f（x）为单调递增函数，f（k·3^x）＜f（-3^x+9^x+2），k·3^x＜9^x-3^x+2，k＜3^x+-1

设u（x）=3^x+-1≥2-1　得k＜2-1

19.

执行程序次数	N	X	y	z
1	1	3	2	3·2
2	2	5	22	3·2+5·22
3	3	7	23	3·2+5·22­+7·22
…	…	…	…
n	n	2n+1	2n	3·2+5·22+7·22+…+（2n+1）·2n

设n=Ii时，x，y，z的值分别为x_i，y_i，z_i，依题意，x₀=1，x_n=x_n-1+2，所以{x_n}是等差数列，且x_n=2n+1，Y₀=1，y_n=2y_n-1，所以{y_n}是等比数列，且y_n=2ⁿ，z₀=0，z_n=z_n-1+x_ny_n，

所以z_n=x₁y₁+x₂y₂+…+x_ny_n=3×2+5×2²+7×2³+…（2n+1）×2ⁿ

用错位相减法求和得：z_n=（2n-1）2ⁿ⁺¹+2

当z_n=（2n-1）2ⁿ⁺¹+2＞7000时，取n=8，此时z=7682。

20. （Ⅰ）f（x）=a（x-）²+1-，由于≤a≤1，所以1≤≤3，

y_小=N（a）=1-，当≤a≤1，即1≤≤2时，y_大=f（3）=9a-5，

当≤a≤，即2≤≤3时，y_大=f（1）=a-1，g（a）=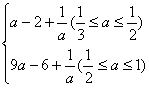

（Ⅱ）g＇（a）=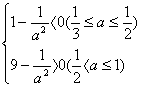

a时，g（a）为减函数；a时，g（a）为增函数，（也可以利用函数y=x+的图像及性质来判断此函数的单调性）。当a=时，g（a）的最小其值为。

21. （Ⅰ）f（1）=log₁₆2=　　f（-2）==1，得a=1，b=0，

f（x）=，（x≠-1）；

（Ⅱ）x₁=3/4，x₂=4/6，x₃=5/8，x₄=6/10。猜想x_n=，并用数学归纳法证明（略）

22. （Ⅰ）f＇（x）=3x²+2bx+c│_x=0=c=0；

（Ⅱ）f（2）=0，8+4b+d=0，d=-8-4b,f＇（x）=3x²+2bx=x（3x+2b）

因为f（x）在（-，0）上是增函数，在[0，2]上是减函数，所以2≤-，b≤-3，

f（1）=1+b-8-4b=-3b-7≥2。

（Ⅲ）f（x）=x³+bx²-4b-8=（x-2）[x²+（b+2）x+4+2b]

│α-β│=

│α-β│的取值范围为[3，+）。