数学能力专题训练（数学归纳法）

数学能力专题训练 (数学归纳法)

要点:

1.数学归纳法是证明有关自然数n的命题的一种数学方法,证明步骤与格式的规范是数学归纳法证题的鲜明特征。

 2.由n=k时命题成立推证n=k+1时命题成立。一是要注意使用归纳假设,

二是要看准目标,有的放矢进行变形。

3.注意不完全归纳法与数学归纳法的区别与联系,初步形成“观察—归纳—猜想—

证明”的思维方法,既能发现结论,又能证明结论,这是分析问题、解决问题能力

的重要内容,也是近年来高考考查的重点。

能力训练:

 1.用数学归纳法证明:“1+++…+<n (n>1)”时,由n=k(k>1)不等式成立,推

证n=k+1时,左边应增加的项数是　　　　　　　　　　　　　　　  (　　)

(A)2^k-1　　　 (B)2^k-1 　　　　(C) 2^k  (D) 2^k+1

 2.球面上有n个大圆,其中任何三个都不相交于同一点,设球面被这n个大圆所分

成的部分为f(n),则下列猜想:①f(n)=n, ②f(n)=f(n-1)+2n, ③f(n)=n²-n+2

中,正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

(A) ①与②　　(B) ①与③　　(C) ②与③　 (D)只有③

3.用数学归纳法证明:当n∈N,1+2+2²+2³+…+2^5n-1是31倍数时,当n=1时,原式为

___________________.从n=k到n=k+1时需增添的项是_______________________.

4.用数学归纳法证明(a,b是非负实数,n∈N⁺)时,假设n=k

时不等式 (*)成立,再推证n=k+1时不等式也成立的关键是将(*)式

__________________.

　 5.求最大的正整数m,使得f(n)=(2n+7)•3ⁿ+9对任意的自然数n,都能被m整除,并

证明你的结论.

6.当n∈N时,S_n=1-+-+…+-,T_n=++…+.对于

相同的n,试比较 S_n与 T_n的大小关系,并证明你的结论.

7.已知函数f(x)=-2+2 (x≥4)

　⑴试求反函数f^-1(x),并指出其定义域;

　⑵如果数列{a_n} (a_n≥0)中a₁=2,前n项和为S_n (n∈N)且S_n=f^-1(S_n-1),求{a_n}的

通项公式;

　⑶求的值.

　　

　

8.设函数y= (n∈N)的最小值为a_n,最大值为b_n,且c_n=,

　⑴求数列{c_n}的通项公式;

　⑵记S_n=++…+,求证:2(-1)<S_n<2

9.设{a_n}是等差数列,b_n=a_na_n+1a_n+2　(n∈N),{b_n}的前n项和用S_n表示,若

{a_n}的公差d=a₁,证明对于任意自然数n都有S_n=(d≠0).

10.在自然数集N上定义函数y=f(n)满足f(n+1)=　(n∈N),

且f(1)=2,是否存在实数a、b,使f(n)=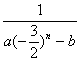+1对任意自然数n恒成

立?并证明你的结论.