北京市海淀区2006年1月高三数学期末考试卷（文科）

北京市海淀区2006年1月高三数学期末考试卷（文科）

一．选择题：

1．已知sin570°的值为（　）

　　（A）　 （B）－　 （C）　 （D）－

2．若直线ax+y－1=0与直线4x+(a－3)y－2=0垂直，则实数a的值等于（　）

　　（A）－1　 （B）4　 （C）　 （D）－

3．函数f(x)= sinxcosx－sin²x的最小正周期为（　）

　　（A）　 （B）　 （C）π　 （D）2π

4．已知向量，满足：=2，=1，，那么向量与的夹角为（　）

　　（A）30°　 （B）45°　 （C）60°　 （D）90°

5．已知两不重合的直线a，b及两不重合的平面α、β，那么下列命题中正确的是（ ）

（A）　 （B）　

（C）　 （D）

6．若椭圆的离心率为，则实数m等于（　）

　　（A）或　 （B）　 （C）　 （D）或

7．甲、乙两人独立地解同一问题，甲解决这个问题的概率是P₁，乙解决这个问题的概率是P₂，则其中至少有一个人解决这个问题的概率为（　）

　　（A）P₁+P₂　 （B）P₁·P₂　 （C）1－P₁·P₂　 （D）1－(1－P₁)(1－P₂)

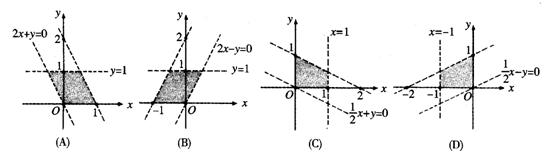
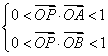8．向量=(1，)，=(0，1)，若动点P(x，y)满足条件：，则P(x，y)的变化范围（不含边界的阴影部分）是（　）

二．填空题：

9．抛物线x²=ay的准线方程是y=2，则实数a的值为　　　　　  。

10．函数y=的图象F按向量平移后，得到图象F’的解析式为，则向量的坐标是　　　　　　 。

11．圆(x+1)²+y²=4上的动点P到直线x+y－7=0的距离的最小值等于　　　　　  。

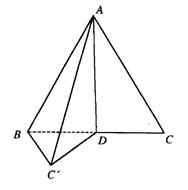12．如图，等边三角形ABC的边长为4，D为BC中点，沿AD把△ADC折叠到△ADC’处，使二面角B－AD－C ’为60°，则折叠后点A到直线B的距离为　　　　　　 ；二面角的正切值为　　　　　  。

13．等腰直角三角形ABC的三个顶点在同一球面上，∠BAC=90°，AB=AC=，若球心O到平面ABC的距离为1，则该球的半径为　　　　  ；球的表面积为　　　　  。

14．对于任意实数x，函数f(x)取x、、7－x三者中的最小值，那么f(x)的最大值是　　　　　　　　　　　  .

三．解答题：　

15．△ABC中角A、B、C的对边分别为a、b、c，，△ABC的面积为且c=， 3cosC－2sin²C=0，求

　　（1）角C的大小；　 （2）a、b的值。

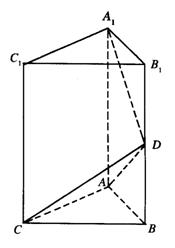16．如图直三棱柱ABC－A₁B₁C₁中，∠BAC=90°，AB=AC=a，AA₁=2a， D为棱BB₁的中点，

（1）证明：A₁C₁//平面ACD；

（2）求异面直线AC与A₁D所成角的大小；

（3）证明：A₁D⊥平面ADC.

17．已知圆C：x²+y²+2x－4y+3=0，

（1）求圆心C的坐标及半径r的大小；

（1）已知不过原点的直线l与圆C相切，且在x轴和y轴上的截距相等，求直线l的方程；

（2）从圆C外一点P(x₁，y₁)向该圆引一条切线，切点为M，O为坐标原点，且有PM=PO，求点P的轨迹方程。

18．数列{a_n}(n∈N^*)中，a₁=1，且a_n+1=2a_n+1，又设b_n=a_n+1，

（1）求证：数列{b_n}是等比数列；

（2）求数列{a_n}的通项公式；

（3）设(n∈N^*)，求数列{c_n}的前n项和S_n.

19．函数f(x)=，在x₁，x₂处有极值f(x₁)、f(x₂)，其中x₁∈(0，1)，x₂∈(1，2)，

（1）证明：f(x₁)为f(x)的极大值；f(x₂)为f(x)的极小值；

（2）求实数a的取值范围.

20．已知双曲线(a>0，b>0)的左右顶点分别为A、B，右焦点为F(c，0) (c>0)，右准线为l：x=，AF=3，过点F作直线交双曲线右支与P、Q两点，延长PB交右准线l于M点，

（1）求双曲线的方程；

（2）若，求△PBQ的面积S；

（3）若，问是否存在实数μ，使得：，若存在，求出μ的值；若不存在，请说明理由。