北京市八中2005—2006学年度上学期高三调研模拟试卷
数学(理科)
一、选择题:
1.若集合![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.复数![]() 的值是
的值是
A .2 B.![]() C.
C.![]() D.
D.![]()
3.设函数 在点
在点![]() 处连续,则
处连续,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.“![]() 且
且![]() ”是“
”是“![]() 且
且![]() ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
5.已知![]() 在区间
在区间![]() 上递增,则实数
上递增,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.![]() ,则
,则![]() 等于天星 教育网
等于天星 教育网
A.1 B.0 C.3 D.![]()
7.曲线![]() 上的点到直线
上的点到直线![]() 的最短距离是
的最短距离是
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
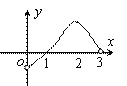 8.已知函数
8.已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() 的图象如图所示,则不等式
的图象如图所示,则不等式![]() 的解集是
的解集是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.设函数![]() 给出下列四个命题:
给出下列四个命题:
①![]() 时,
时,![]() 是奇函数;
是奇函数;
②![]() 时,方程
时,方程![]() 只有一个实根;
只有一个实根;
③![]() 的图象关于
的图象关于![]() 对称;
对称;
④方程![]() 至多有两个实根.
至多有两个实根.
其中正确的命题是
A.①④ B.①③ C.①②③ D.①②④
10.正实数![]() 及函数
及函数![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为
A.4 B.2 C.![]() D.
D.![]()
二、填空题:
11.国家准备出台调整个人收入所得税方面的政策,各地举行各行业收入的入户调查.某住宅小区约有公务员120,公司职员200人,教师80人,现采用分层抽样的方法抽取容量为20人的样本进行调查,则公务员、公司职员、教师各抽取的人数为 .
12.已知函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() ,
,![]() 的反函数是
的反函数是![]() ,则
,则![]() =
.
=
.
13.曲线![]() 在点
在点![]() 处的切线方程为
.
处的切线方程为
.
14.购买手机的“全球通”卡,使用须付“基本月租费”(每月须交的固定费用)50元,在市区通话时每分钟另收话费0.40元;购买“神州行”卡,使用时不收“基本月租费”,但在市区通话时每分钟话费0.60元,若某用户每月手机费预算为120元,则在这两种手机卡中,购买 卡较合算.
三、解答题:
15.已知集合![]() ,集合
,集合![]() ,若
,若![]() ,求实数
,求实数![]() 的值.
的值.
16.某校一个研究性学习团队从网上查得,某种植物种子在一定条件下的发芽成功的概率为![]() ,于是该学习团队分两个小组进行验证性实验.
,于是该学习团队分两个小组进行验证性实验.
(1)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;
(2)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则就继续进行下次实验.直到种子发芽成功为止,但实验的次数不超过5次.求这一小组所做的种子发芽实验次数![]() 的分布列和期望.
的分布列和期望.
17.已知命题![]() :复数
:复数![]() 对应的点落在复平面的第二象限;命题
对应的点落在复平面的第二象限;命题![]() :以
:以![]() 为首项,公比为
为首项,公比为![]() 的等比数列的前
的等比数列的前![]() 项和极限为2.若命题“
项和极限为2.若命题“![]() 且
且![]() ”是假命题,“
”是假命题,“![]() 或
或![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围.
的取值范围.
18.设函数![]() 是奇函数(
是奇函数(![]() 都是整数,且
都是整数,且![]() ,
,![]() ,
,![]() 在
在![]() 上是单调递增.
上是单调递增.
(1)求![]() 的值;
的值;
(2)当![]() ,
,![]() 的单调性如何?用单调性定义证明你的结论.
的单调性如何?用单调性定义证明你的结论.
19.函数![]() 对任意实数
对任意实数![]() 都有
都有![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值,猜想
的值,猜想![]() 的表达式并用数学归纳法证明你的结论;
的表达式并用数学归纳法证明你的结论;
(3)若![]() ,求证:
,求证:![]() .
.
天星 教育网
20.已知![]() 函数
函数![]() 的图像与函数
的图像与函数![]() 的图象相切.
的图象相切.
(1)求b与c的关系式(用c表示b);
(2)设函数![]() ,
,
(ⅰ)当![]() 时,在函数
时,在函数![]() 的图像上是否存在点
的图像上是否存在点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(ⅱ)若函数![]() 在
在![]() 内有极值点,求c的取值范围.
内有极值点,求c的取值范围.
北京八中理科参考答案及评分标准
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | D | A | B | D | A | B | C | C |
11.6、10、4 12. -2 13. y=2x 14.神州行
15. ![]() ,
, ![]()
![]()
则有![]() 或
或![]()
16.(1)至少有3次成功包括3次、4次和5次成功,即
![]()
(2)依题意有
| | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
![]()
17.命题![]() 有:
有: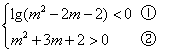
由①得:![]()
由②得:![]()
由上得满足P的m的取值范围是:![]() 或
或 ![]()
对命题![]() ,有:
,有:![]() , 又
, 又![]() ,得:
,得:![]() 且
且![]()
又命题“![]() 且
且![]() ”是假命题,“
”是假命题,“![]() 或
或![]() ”是真命题,则
”是真命题,则
m的范围是 ![]()
18.(1)由![]() 是奇函数,得
是奇函数,得![]() 对定义域内x恒成立,则
对定义域内x恒成立,则
![]() 对对定义域内x恒成立,即
对对定义域内x恒成立,即![]()
(或由定义域关于原点对称得![]() )
)
又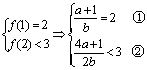 由①得
由①得![]() 代入②得
代入②得![]() ,
,
又![]() 是整数,得
是整数,得![]()
(2)由(1)知,![]() ,当
,当![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.下用定义证明之.
上单调递减.下用定义证明之.
设![]() ,则
,则![]()
![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() 在
在![]() 上单调递增;
上单调递增;
同理,可证![]() 在
在![]() 上单调递减.
上单调递减.
19.(1)令![]() 得
得![]()
(2)![]() ,
, 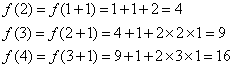
猜想![]() ,下用数学归纳法证明之.(略)
,下用数学归纳法证明之.(略)
(3)![]() ,则
,则![]()
假设![]() 时命题成立,即
时命题成立,即![]() ,则
,则
![]() ,
,
由上知,则![]() . 天星 教育网
. 天星 教育网
20.(1)依题意,令![]()
![]()
(2)![]()
(ⅰ)当![]() 时,
时,![]() ,
,![]()
![]() ,若存在满足条件的点M,则有:
,若存在满足条件的点M,则有:
![]() ,
,![]() ,即这样的点M存在,且坐标为
,即这样的点M存在,且坐标为![]()
(ⅱ)![]()
令![]() (x)=0,即3x2+4bx+b2+c=0;而
(x)=0,即3x2+4bx+b2+c=0;而![]() =16b2-12(b2+c)=4(b2-3c),
=16b2-12(b2+c)=4(b2-3c),
若![]() =0,则
=0,则![]() (x)=0有两个相等的实根,设为x0,此时
(x)=0有两个相等的实根,设为x0,此时![]() (x)的变化如下:
(x)的变化如下:
| x |
| x0 | ( |
|
| + | 0 | + |
于是![]() 不是函数
不是函数![]() 的极值点.
的极值点.
![]() 的变化如下:
的变化如下:
| x |
| x1 |
|
| ( |
|
| + | 0 | — | 0 | + |
由此,x=x1是函数F(x)的极大值点,x=x2是函数F(x)的极小值点.
综上所述,当且仅当![]()
