河北省石家庄市高中毕业班复习教学质量检测(二)
数学试卷
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.方程![]() 、
、![]() )的解集为( )
)的解集为( )
A.![]() B.{0}
B.{0}
C.![]() D.
D.![]()
2.复数![]() ,则
,则![]() 在复平面内的对应点位于( )
在复平面内的对应点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.设![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() 等于( )
等于( )
A.3 B.9 C.21 D.39
4.对于直线![]() 、
、![]() 和平面
和平面![]() 、
、![]() ,
,![]() 的一个充分条件为( )
的一个充分条件为( )
A.![]() ∥
∥![]() ∥
∥![]() B.
B.![]()
C![]() ∥
∥![]() D.
D.![]() ∥
∥![]()
5.在锐角![]() 中,若
中,若![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.(1,
B.(1,![]() )
)
C.![]() D.(―1,1)
D.(―1,1)
6.函数![]() 的一条对称的方程为
的一条对称的方程为![]() ,则以向量
,则以向量![]() 为方向向量的直线的倾斜角为( )
为方向向量的直线的倾斜角为( )
A.45° B.60° C.120° D.135°
7.若椭圆![]() 按向量
按向量![]() 平移后所得方程为
平移后所得方程为![]() ,则向量
,则向量![]() 等于( )
等于( )
A.(1,-2) B.(1,2)
C.(-1,2) D.(―1,―2)
8.与双曲线![]() 有共同的渐近线,且经过点(-3,
有共同的渐近线,且经过点(-3,![]() )的双曲线方程是( )
)的双曲线方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.给出以下四个命题:
①若![]() ,则
,则![]() 的取值范围是(1,
的取值范围是(1,![]() ) ②函数
) ②函数![]()
![]() 的单调递减区间为
的单调递减区间为![]() ③不等式
③不等式![]() 的解集为(0,1) ④若
的解集为(0,1) ④若![]() ,则
,则![]()
以上四个命题中正确命题的序号为( )
A.①④ B.③④ C.②③ D.①②
10.在正方体![]() 中,
中,![]() 是底面
是底面![]() 的中心,
的中心,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,则直线
的中点,则直线![]() ( )
( )
A.是![]() 和
和![]() 的公垂线
的公垂线
B.垂直于![]() ,但不垂直于
,但不垂直于![]()
C.垂直于![]() ,但不垂直于
,但不垂直于![]()
D.与![]() 、
、![]() 都不垂直
都不垂直
11.(理)设定义域、值域均为![]() 的函数
的函数![]() 的反函数为
的反函数为![]() ,且
,且![]() ,则
,则![]() 的值为( )
的值为( )
A.2 B.0 C.-2 D.![]()
(文)已知![]() ],则此函数的反函数为( )
],则此函数的反函数为( )
A.![]()
B.![]()
C.![]()
D.![]()
12.某科研单位,欲拿出一定的经费奖励科研人员,第一名得全部奖金的一半多一万元,第二名得剩下的一半多一万元,以名次类推都得到剩下的一半多一万元,到第七名恰好将奖金分完,则需拿出奖金( )
A.250万元 B.252万元
C.254万元 D.256万元
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
13.设![]() 、
、![]() 是两个不共线的向量,则向量
是两个不共线的向量,则向量![]() 与向量
与向量![]() 共线的充要条件是____________.
共线的充要条件是____________.
14.已知点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 、
、![]() 是圆
是圆![]() 的两条切线,
的两条切线,![]() 为切点,
为切点,![]() 为圆心,则当四边形
为圆心,则当四边形![]() 的面积最小时点
的面积最小时点![]() 的坐标为__________.
的坐标为__________.
15.已知两变量![]() 、
、![]() 之间的关系为
之间的关系为![]() ,则以
,则以![]() 为自变量函数
为自变量函数![]() 的最小值为__________.
的最小值为__________.
16.四个不同的球,放入四个不同的盒子中,恰有两个空盒的放法种数是___________.
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
(理)一袋中装有6张同样的卡片,上面分别标有1,2,3,4,5,6,现从中随机取出3张卡片,以![]() 表示取出的卡片中的最大标号.
表示取出的卡片中的最大标号.
(1)求![]() 的分布列;
的分布列;
(2)求![]() .
.
(文)某班甲、乙、丙三名同学竞选班委,甲当选的概率为![]() ,乙当选的概率为
,乙当选的概率为![]() ,丙当选的概率为
,丙当选的概率为![]() .
.
(1)求甲、乙、丙恰有一名同学当选的概率;
(2)求甲、乙、丙至多两人当选的概率.
18.(本小题满分12分)
已知![]() ,若
,若![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
19.(本小题满分12分)
如右图,正三棱柱![]() 的所有棱长均为2,
的所有棱长均为2,![]() 是棱
是棱![]() 上的一动点.
上的一动点.
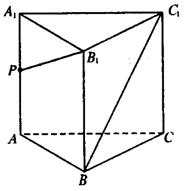
(1)当![]() 在棱
在棱![]() 上运动时,
上运动时,![]() 是否有能与平面
是否有能与平面![]() 垂直,说明理由;
垂直,说明理由;
(2)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)在(2)的条件下,求二面角![]() 的大小.(文科只需求出该角的一个三角函数值).
的大小.(文科只需求出该角的一个三角函数值).
20.(本小题满分12分)
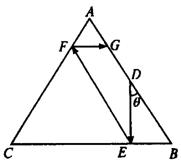
一张形状为等边三角形的球桌,设其顶点为![]() 一个球从
一个球从![]() 边的中点
边的中点![]() 击出,击中
击出,击中![]() 边上的某点
边上的某点![]() ,并且依次碰出
,并且依次碰出![]() 边于点
边于点![]() ,最后击中
,最后击中![]() 边于点
边于点![]() ,设
,设![]() ,求
,求![]() 的取值范围.
的取值范围.
(文科只需求出![]() 的取值范围)
的取值范围)
21.(本小题满分12分)
设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线分别交椭圆和
垂直的直线分别交椭圆和![]() 轴正半轴于
轴正半轴于![]() ,
,![]() 两点,且
两点,且![]() 分向量
分向量![]() 所成的比为8∶5.
所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() :
:![]() 相切,求椭圆方程.
相切,求椭圆方程.
22.(本小题满分14分)
(理)给定正整数![]() 和正数
和正数![]() ,对于满足条件
,对于满足条件![]() 的所有无穷等差数列
的所有无穷等差数列![]() ,试求
,试求![]() 的最大值,并求出
的最大值,并求出![]() 取最大值时
取最大值时![]() 的首项和公差.
的首项和公差.
(文)给定正整数![]() 和正数
和正数![]() ,对于满足条件
,对于满足条件![]() 的所有无穷等差数列
的所有无穷等差数列![]() ,试求
,试求![]() 的最大值,并求出
的最大值,并求出![]() 取最大值时
取最大值时![]() 的首项和公差.
的首项和公差.
参考答案
一、1.C 2.D 3.D 4.C 5.A 6.D 7.C 8.A 9.B 10.A 11.(理)B (文)C 12.C
二、13.![]() 14.(-3,-3) 15.4 16.84
14.(-3,-3) 15.4 16.84
三、17.(理)解:(1)![]() ;
;
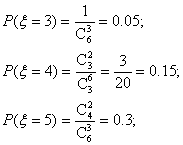
![]() . 4分
. 4分
所以![]() 的分布列为
的分布列为
|
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 0 | 0 | 0.05 | 0.15 | 0.3 | 0.5 |
8分
(2)![]() . 12分
. 12分
(文)解:设甲、乙、丙当选的事件分别为![]() 、
、![]() 和
和![]() .
.
(1)![]() . 3分
. 3分
因为事件![]() 相互独立,恰有1名同学当选的概率为
相互独立,恰有1名同学当选的概率为
![]()
![]()
![]() 8分
8分
![]() .
.
答:恰有一名同学当选的概率为![]() . 9分
. 9分
(2)至多有两人当选的概率为
![]()
![]() . 12分
. 12分
18.解:当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 恒成立. 2分
恒成立. 2分
设![]() ,
,
则![]() . 4分
. 4分
由![]() 得
得![]() 或
或![]() . 5分
. 5分
∴当![]() 时,
时,![]() ,此时
,此时![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,此时
,此时![]() 为减函数; 7分
为减函数; 7分
当![]() 时,
时,![]() ,此时
,此时![]() 为增函数. 8分
为增函数. 8分
∴![]() ,
,
又∵![]() .
.
∴当![]() 时,
时,![]() 有最大值2. 10分
有最大值2. 10分
由![]() 得
得![]() 或
或![]() . 12分
. 12分
19.解:(1)无论![]() 在
在![]() 的任何位置
的任何位置![]() 都不能与平面
都不能与平面![]() 垂直.
垂直.
反证法:假设![]() 平面
平面![]() ,则
,则![]() ,必有
,必有![]() 与
与![]() 重合;
重合;![]() 平面
平面![]() ,则必有
,则必有![]() ,即
,即![]() 与
与![]() 矛盾. 3分
矛盾. 3分
(2)连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,又
,又![]() , 4分
, 4分
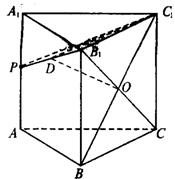
∴![]() 平面
平面![]() ,且垂足为
,且垂足为![]() .
.
∴![]() .取
.取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() 面
面![]() 而
而![]() 为
为![]() 在面
在面![]() 内的射影,由三垂线逆定理知
内的射影,由三垂线逆定理知![]() ,而四边形
,而四边形![]() 为正方形, 7分
为正方形, 7分
∴易见![]() 为棱
为棱![]() 的中点.
的中点.
∴![]() . 8分
. 8分
(3)由(2)知,![]() 面
面![]() ,过
,过![]() 作
作![]() 于
于![]() ,连
,连![]() 则
则![]() 所求二面角的平面角, 9分
所求二面角的平面角, 9分
在![]() 中(如右图)
中(如右图)![]() ,
,
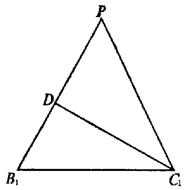
∴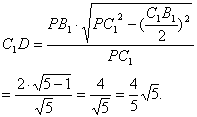
在![]() 中,
中,![]() ,
,
![]() . 11分(文12分)
. 11分(文12分)
∴所求二面角大小是![]() . 12分
. 12分
20.解:由![]() 为等边三角形及入射角等于反射角易见
为等边三角形及入射角等于反射角易见![]() ∽
∽![]() ∽
∽![]() ,2分
,2分
∴![]() . 3分
. 3分
不失一般性,设等边![]() 的边长为2,且
的边长为2,且![]() ,
,
则有![]() ,且
,且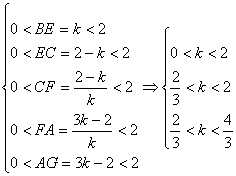
![]() . 8分
. 8分
在![]() 中,由正弦定理得
中,由正弦定理得
![]()
![]() . 10分
. 10分
而![]() , (文12分)
, (文12分)
即![]() . 12分
. 12分
21.解:(1)设点![]() 其中
其中![]() .
.
由![]() 分
分![]() 所成的比为8∶5,得
所成的比为8∶5,得![]() , 2分
, 2分
∴![]() .①, 4分
.①, 4分
而![]() ,
,
∴![]() .
.![]() .②, 5分
.②, 5分
由①②知![]() .
.
∴![]() . 6分
. 6分
(2)满足条件的圆心为![]() ,
,
![]() , 8分
, 8分
圆半径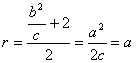 . 10分
. 10分
由圆与直线![]() :
:![]() 相切得,
相切得,![]() ,
,
又![]() .
.
∴椭圆方程为![]() . 12分
. 12分
22.(理)解:设![]() 公差为
公差为![]() ,则
,则![]() . 3分
. 3分
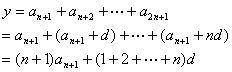
![]() 4分
4分
![]()
![]() . 7分
. 7分
又![]() .
.
∴![]() ,当且仅当
,当且仅当![]() 时,等号成立. 11分
时,等号成立. 11分
∴![]() . 13分
. 13分
当数列![]() 首项
首项![]() ,公差
,公差![]() 时,
时,![]() ,
,
∴![]() 的最大值为
的最大值为![]() . 14分
. 14分
(文)解:设![]() 公差为
公差为![]() ,则
,则![]() . 3分
. 3分
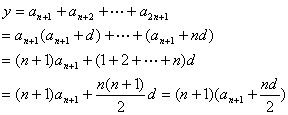
![]() , 6分
, 6分
又![]() .
.
∴![]() .
.
当且仅当![]() 时,等号成立. 11分
时,等号成立. 11分
∴![]() . 13分
. 13分
当数列![]() 首项
首项![]() ,公差
,公差![]() 时,
时,![]() .
.
∴![]() 的最大值为
的最大值为![]() . 14分
. 14分