中山市桂山中学06届高三11月月考数学试题
时间:100分钟 命题人:肖定涛
第Ⅰ卷 (试题卷)
一,选择题 (每小题5分共50分)
1,已知平面向量![]() ,
,![]() ,且
,且![]() ⊥
⊥![]() , 则
, 则![]()
![]() 3
3 ![]()
![]() -1
-1![]()
![]() -3
-3
2,如果复数![]() 的实部与虚部互为相反数,那么实数
的实部与虚部互为相反数,那么实数![]() 等于
等于
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
3,从五名学生中选出4名分别参加数学、物理、化学、英语竞赛,则不同参赛方案种数为
![]()
![]()
![]()
![]()
4,设![]() 为三角形的一个内角,且
为三角形的一个内角,且![]() ,则
,则![]()
![]()
![]()
![]()
![]()
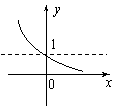

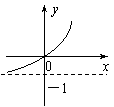
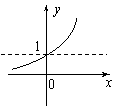 5,函数
5,函数![]() 的反函数图象是
的反函数图象是
![]()
![]()
![]()
![]()
6,已知直线![]() 、m,平面
、m,平面![]() 、β,且
、β,且![]() 给出下列命题
给出下列命题
①若![]() ∥β,则
∥β,则![]() ②若
②若![]() ,则
,则![]() ∥β ③若
∥β ③若![]() ⊥β,则
⊥β,则![]() //m
//m
④若![]() ∥m,则
∥m,则![]() ⊥β,其中正确命题的个数是
⊥β,其中正确命题的个数是
![]()
![]()
![]()
![]()
7,设函数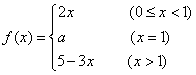 在区间
在区间![]() 上连续,则实数
上连续,则实数![]() 的值为
的值为
![]()
![]()
![]()
![]()
8,为了得到函数![]() 的图象,可以将函数
的图象,可以将函数![]() 的图象
的图象
![]() 向右平移
向右平移![]() 个单位长度
个单位长度 ![]() 向右平移
向右平移![]() 个单位长度
个单位长度
![]() 向左平移
向左平移![]() 个单位长度
个单位长度 ![]() 向左平移
向左平移![]() 个单位长度
个单位长度
本试卷共4页之第1页
9,{![]() }满足
}满足![]() ,
,![]() ,则
,则![]() 等于
等于
![]()
![]()
![]()
![]()
![]()
![]()
![]() 以上都不对
以上都不对
10,设函数![]() 为定义在实数集上单调递增的奇函数,若
为定义在实数集上单调递增的奇函数,若![]() 时,不等式
时,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
![]()
![]()
![]()
![]()
二,填空题 (每小题4分共16分)
11, 函数![]() 的单调递减区间为
;(用区间表示)
的单调递减区间为
;(用区间表示)
12,在![]() 内形如
内形如![]() 的所有整数的和为
;(用具体数字表示)
的所有整数的和为
;(用具体数字表示)
13,已知![]() 是锐角,且
是锐角,且![]() ,则
,则![]() ;
;
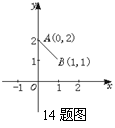
14,设函数![]() 是最小正周期为2的偶函数,它在区间
是最小正周期为2的偶函数,它在区间![]() 上的图象
上的图象
为如图所示的线段,则在区间[1,2]上![]() ;
;
本试卷共4页之第2页
三,解答题 (共84分)
15,(满分14分)已知函数![]()
![]()
(1)求函数![]() 的最小正周期与最大值; (7分)
的最小正周期与最大值; (7分)
(2)当![]() 时,求函数
时,求函数![]() 的单调递增区间; (7分)
的单调递增区间; (7分)
16,(满分14分)从4名男生和2名女生中任选3人参加演讲比赛,设随机变量![]() 表示所选3人中女生的人数,
表示所选3人中女生的人数,
(1)求所选3人中女生人数为0的概率;(4分)
(2)求![]() 的分布列;并求
的分布列;并求![]() 的数学期望;(6分)
的数学期望;(6分)
(3)求“所选3人中女生人数![]()
![]() ”的概率;(4人)
”的概率;(4人)
17,(满分14分)如图:在四棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为正方形,
为正方形,![]() 分别是
分别是![]() 的中点,
的中点,
(1)求证:![]() ⊥
⊥![]() ;(4分)
;(4分)
(2)在平面![]() 内求一点
内求一点![]() ,使
,使![]() ⊥平面
⊥平面![]() ,并证明你的结论;(5分)
,并证明你的结论;(5分)
(3)求![]() 与平面
与平面![]() 所成角的大小;(用反正弦表示)(5分)
所成角的大小;(用反正弦表示)(5分)

本试卷共4页之第3页
18,(满分14分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
![]()
(1)求数列![]() 的通项公式,并求
的通项公式,并求![]() ;(7分)
;(7分)
(2)设![]() ,求
,求![]() ;(7分)
;(7分)
19,(满分14分)已知![]() ,
,
(1)求函数![]() 的定义域;(4分)
的定义域;(4分)
(2)判断函数的奇偶性并加以证明;(5分)
(3)判断函数![]() 在
在![]() 内的单调性并加以证明;(5分)
内的单调性并加以证明;(5分)
20,(满分14分) 已知函数![]() ,
,
(1)求函数![]() 的值? (4分)
的值? (4分)
(2)若数列![]() 的通项公式为
的通项公式为![]() ,
,![]() ,
,
求数列![]() 的前100项和
的前100项和![]() ; (5分)
; (5分)
(3)若数列![]() 的通项公式为
的通项公式为![]() ,
,![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() ,又设数列满足:
,又设数列满足:![]() ,且
,且![]() ,若
,若![]() 满足对任意不小于2的正整数
满足对任意不小于2的正整数![]() ,都有
,都有![]() 恒成立,试求
恒成立,试求![]() 的最大值? (5分)
的最大值? (5分)
![]() 中山市桂山中学2006届高三11月月考数学试卷
中山市桂山中学2006届高三11月月考数学试卷
二、填空题(每小题4分,共16分)
11、 (1, 2) 12、 2046
13、 ![]() 14、
14、 ![]()
三、解答题:(共84分,每小题14分, 解答题要写出解题过程,注意适当的文字叙述。)
15,(1)解:![]() (2分)
(2分)
![]() (5分)
(5分)
故![]() , (6分)
, (6分) ![]() (7分)
(7分)
(2)解:![]() (10分)
(10分)
![]() (12分)
(12分)
故增区间为![]() (14分)
(14分)
16,(1)解:设“所选3人中女生人数为![]() ”,则 (1分)
”,则 (1分)
![]() (3分)
(3分)
答:所选人数中女生人数为0时的概率为![]() (4分)
(4分)
(2)解:![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
|
|
|
|
|
![]() (1分)
(1分)
![]() (2分)
(2分)
![]() (3分) 列出表格(6分)
(3分) 列出表格(6分)
(3)解:设“所选3人中女生人数![]() ”为事件“
”为事件“![]() ”(1分)则
”(1分)则
![]() (3分)
(3分)
答:所选3人中女生人数![]() 的概率为
的概率为![]() (4)
(4)
本答题卷共4页之第1页
 17(1)解:如图所示建立直角坐标系
17(1)解:如图所示建立直角坐标系
![]()
![]() (2分)
(2分)
![]() ⊥
⊥![]() (4分)
(4分)
(2)解:设![]() (1分)
(1分)
又![]()
故![]()
![]() 故
故 ![]() (4分)
(4分)
所以点![]() 为线段
为线段![]() 的中点
(5分)
的中点
(5分)
(3)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又![]()
故而有
![]() (2分)
(2分)
设![]() ,则
,则![]()
所以![]() (3分)
(3分)
又因为![]() ,设
,设![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
则![]() (4分)
(4分)
故所求线面角为 ![]() (5分)
(5分)
本答题卷共4页之第2页
18,(1)解:当![]() 时,
时,
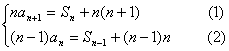 (2分)
(2分)
![]()
![]()
![]()
![]() (3分)
(3分)
当![]() 时,
时,![]() 所以
所以 ![]()
故![]() 为等差数列 ,得出
为等差数列 ,得出![]() (5分)
(5分)
![]() (7分)
(7分)
(2)解:
![]() (5分)
(5分)
所以![]() (7分)
(7分)
19 (1)解:由题意得
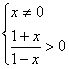 (2分)
(2分)
![]() (4分)
(4分)
(2)解:(1)判断:函数在定义域上为奇函数 (1分)
(2)证明:
由上述可知函数的定义域为 ![]() (2分)
(2分)
因为 ![]()
所以函数在定义域上为奇函数 (5分)
(3)解:(1)判断:函数在![]() 上为减函数
(1分)
上为减函数
(1分)
(2) 证明
![]()
![]() 函数
函数![]() 在
在![]() 上为减函数
(5分)
上为减函数
(5分)
本答题卷共4页之第3页
20 (1)
解:![]() (4分)
(4分)
(2)
解:![]() (1)
(1)
![]() (2)
(2)
![]()
![]() (4分)
(4分)
故而 ![]() (5分)
(5分)
(3)解:
由(2)式的方法,得出![]() (1分)
(1分)
![]()
![]() ,
,
所以数列![]() 为递增的正数数列
为递增的正数数列
故而![]() 的最小值为
的最小值为 ![]() (2分)
(2分)
又因为![]() ,所以
,所以 ![]() (3分)
(3分)
所以![]() 恒成立即只要
恒成立即只要![]() 即可
即可
从而有 ![]()
![]() (4分)
(4分)
所以![]() 的最大值为
的最大值为 ![]() (5分)
(5分)
一,选择题答案为
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | C | B | B | B | B | A | A | C |
本试卷共4页之第4页