江苏省车桥高级中学2006届高三阶段测试
数 学 2005.1120
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. .若直线![]() 和直线
和直线![]() 关于直线
关于直线![]() 对称,
对称,
那么直线![]() 恒过定点
( )
恒过定点
( )
A.(2,0) B.(1,-1) C.(1,1) D.(-2,0)
2圆2x2+2y2=1与直线xsinθ+y-1=0(θ≠![]() +kπ,k∈Z)的位置关系
( )
+kπ,k∈Z)的位置关系
( )
A.相交 B.相切 C.相离 D.不确定
3.设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于
( )
等于
( )
A.18 B.36 C.45 D.60
4.函数![]() 的反函数
( )
的反函数
( )
A.在![]() 上单调递增 B.在
上单调递增 B.在![]() 上单调递减
上单调递减
C.在![]() 上单调递增 D.在
上单调递增 D.在![]() 上单调递减
上单调递减
5.设![]() 均为非空集合,且满足
均为非空集合,且满足![]() ,则下列各式中错误的是 ( )
,则下列各式中错误的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.命题![]() :
:![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
命题![]() :在
:在![]() 中,如果
中,如果![]() ,那么
,那么![]() 为直角三角形.则 ( )
为直角三角形.则 ( )
A.“![]() 或
或![]() ”为假 B.“
”为假 B.“![]() 且
且![]() ”为真 C.
”为真 C.![]() 假
假![]() 真 D.
真 D.![]() 真
真![]() 假
假
7. 经过点M(0,2)且和x轴相切的面积最小圆为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.函数![]()
![]() 的图象的大致形状是
( )
的图象的大致形状是
( )
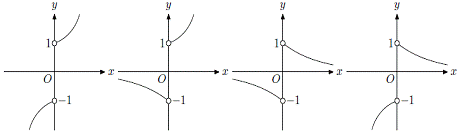
A B C D
9.过(2,1)点的直线中被x2+y2-2x+4y=0截得的最长弦所在的直线方程是 ( )
A.3x-y-5=0 B.3x+y-7=0 C.x+3y-3=0 D.x-3y+1=0
10.在![]() 中,
中,![]() ,则
,则![]() 边上的高为
( )
边上的高为
( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
11. P(x,y)是曲线(x+1)2+y2=1上任意一点,则(x-2)2+(y+4)2的最大值是多少 ( )
A.36 B.6 C.26 D.25
12. 已知函数![]() 为奇函数,函数
为奇函数,函数![]() 为偶函数,且
为偶函数,且![]() ,则
,则![]() =
=
( )
A.2 B.-2 C.4 D.-4
第Ⅱ卷(非选择题 共90分)
二.填空题:本大题共6小题,每小题4分,共24分.把答案填写在答题卡相应的位置上.
13. 已知集合![]() ,
,![]() ,若
,若![]() ,
,
则实数![]() 的取值范围是
.
的取值范围是
.
14.已知平面向量![]() ,若
,若![]() ,则实数
,则实数![]() .
.
15.已知直线过点P(-4,-3)且被(x+1)2+(y+2)2=25截得的弦长为8则L的方程是 .
16. P是直线3x+4y+8=0上的动点;PA是圆x2+y2-2x-2y +1=0的切线,点A为切点,PA最短时的值为 .
17.在条件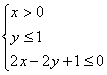 下,目标函数S=2x+y的最大值为
.
下,目标函数S=2x+y的最大值为
.
18.若![]() 为
为![]() 的各位数字之和
的各位数字之和![]() .如:因为
.如:因为
![]() ,所以
,所以![]() .记
.记![]() ,
,
![]() ,……,
,……,![]() ,
,![]() ,则
,则![]() =
.
=
.
三.解答题:本大题共5小题,共66分.解答应写出文字说明、证明过程或演算步骤.
19.(本小题满分12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调减区间;
的单调减区间;
(Ⅱ)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(Ⅲ)若函数![]() 的图象按向量
的图象按向量![]()
![]() 平移后得到函数
平移后得到函数![]() 的图象,求实数
的图象,求实数![]() 的值.
的值.
20.(本题满分12分)
已知数列![]() 的前n项和为
的前n项和为![]()
(Ⅰ)求![]() ; (Ⅱ)求数列
; (Ⅱ)求数列![]() 的通项。
的通项。
21.(本小题满分12分)
在![]() 中,
中,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 的面积最大时,求
的面积最大时,求![]() 的大小.
的大小.
22.(本题满分12分)
如图,圆![]() 与圆
与圆![]() 的半径都是1,
的半径都是1,![]() ,过动点P分别作圆
,过动点P分别作圆![]() 、圆
、圆![]() 的切线PM、PN(M、N分别为切点),使得
的切线PM、PN(M、N分别为切点),使得![]() 。试建立适当的坐标系,并求动点P的轨迹方程。
。试建立适当的坐标系,并求动点P的轨迹方程。

.
23(本小题满分14分)
已知函数![]() ,并且
,并且![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在各项均不为零的数列![]() ,满足
,满足![]() (
(![]() 为数列
为数列![]() 的前
的前![]() 项和).若有,写出数列的一个通项公式
项和).若有,写出数列的一个通项公式![]() ,并说明满足条件的数列
,并说明满足条件的数列![]() 是否唯一确定;若无,请说明理由.
是否唯一确定;若无,请说明理由.
命题:李建华
审核:李建华
淮安市车桥中学2006届高三阶段测试
数学试卷参考答案
2005.11.20
一、选择题:(5分×12=60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | C | D | C | D | A | D | A | A | A | B |
二、填空题:(4分×6=24分)
13、 [-1,6] ;14、 3或-1 ;15、3y+4x+25=0或x= -4 ;
16、
2![]() ;17、
2
;18、
11
;
;17、
2
;18、
11
;
三.解答题:本大题共5小题,共66分.解答应写出文字说明、证明过程或演算步骤.
19.(本小题满分12分)
解:(Ⅰ)![]() ……………………………………………………………1分
……………………………………………………………1分
![]()
![]() .……………………………………………………………2分
.……………………………………………………………2分
令 ![]() ,…………………………………………3分
,…………………………………………3分
得 ![]() .
.
因此,函数![]() 的单调减区间为
的单调减区间为![]() .………………………5分
.………………………5分
(Ⅱ)当![]() 时,
时,![]() ,………………………………………………6分
,………………………………………………6分
∴ ![]() .……………………………………………………………7分
.……………………………………………………………7分
因此,函数![]() 的值域为
的值域为![]() .……………………………………………………8分
.……………………………………………………8分
(Ⅲ)函数![]() 的图象按向量
的图象按向量![]()
![]() 平移后得到的图象对应的函数是
平移后得到的图象对应的函数是![]() .……………………………………10分
.……………………………………10分
令 ![]() ,得
,得 ![]() .…………………………………12分
.…………………………………12分
20.(本题满分13分)
(1)∵![]()
∴当n=1时,![]() =a1 ∴a1=
=a1 ∴a1=![]() ;……3分
;……3分
当n=2时,![]() ∴
∴![]() ……6分
……6分
(2)∵![]() ∴
∴![]()
∴![]() ……8分
……8分
∴![]() ∴
∴![]() ……10分
……10分
又当n=1时,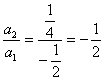 ……11分
……11分
∴{an}为等比数列,且首项与公比都为![]()
∴![]() ……12分
……12分
21.(本题满分13分)
(Ⅰ)由已知得
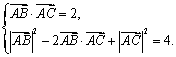 ……………………………………………………………3分
……………………………………………………………3分
因此,![]() .……………………………………………………………… 4分
.……………………………………………………………… 4分
(Ⅱ)![]() ,…………………………………………………………6分
,…………………………………………………………6分
![]()
![]()
![]()
![]() ………………………………………………………………8分
………………………………………………………………8分

![]() .…………………………………………………10分
.…………………………………………………10分
(当且仅当![]() 时,取等号)…………………11分
时,取等号)…………………11分
当![]() 的面积取最大值
的面积取最大值![]() 时,
时,![]() ,
,![]() .………………12分
.………………12分
22.(本题满分14分)
以![]()
![]() 的中点O为原点,
的中点O为原点,![]()
![]() 所在的直线为x轴,建立平面直角坐标系,则
所在的直线为x轴,建立平面直角坐标系,则![]() (-2,0),
(-2,0),![]() (2,0),
(2,0),
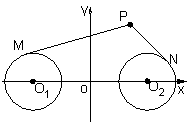 由已知
由已知![]() ,得
,得![]()
![]()
因为两圆的半径均为1,所以
![]()
![]()
设![]() ,则
,则![]() ,
,
即![]() ,
,
所以所求轨迹方程为![]()
![]() (或
(或![]() )
)![]()
23.(本题满分14分)
解:(Ⅰ)由![]() ,得
,得![]() .
.
由![]() ,
,![]() ,得
,得
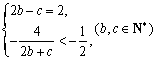 ,即
,即![]() .……………………………3分
.……………………………3分
解得 ![]() .
.
因此,![]() ,
,![]() .……………………………………………………………5分
.……………………………………………………………5分
(Ⅱ)由(Ⅰ)得![]() .当
.当![]() 且
且![]() 时,
时,![]() ,
,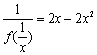 .
.
设存在各项均不为零的数列![]() ,满足
,满足![]() .则
.则
![]() ,即
,即![]() (
(![]() 且
且![]() ).…………………………6分
).…………………………6分
首先,当![]() 时,
时,![]() ;……………………………………………………7分
;……………………………………………………7分
由
![]() ,
,![]() ,得
,得
![]() ,即
,即
![]() .……………………………………………………………9分
.……………………………………………………………9分
若
![]() ,则由
,则由![]() ,得
,得![]() ,这与
,这与![]() 矛盾.………………………10分
矛盾.………………………10分
若
![]() ,则
,则 ![]() .
.
因此,![]() 是首项这
是首项这![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
通项公式为
![]() .
.
综上可得,存在数列![]() ,
,![]() 符合题中条件.…………………………………11分
符合题中条件.…………………………………11分
由上面的解答过程可知,数列![]() 只要满足条件
只要满足条件![]() 即可.
即可.
因此,可以数列一部分满足![]() ,另一部分满足
,另一部分满足![]() ,且保证
,且保证![]() 且
且![]() .
.
例如:数列 ![]() ;
;
数列 ![]()
因此,满足条件的数列不唯一.…………………………………………14分