纪念中学2006届高三第二次阶段性考试
数学试题 2005.11.26
一、选择题
1.若集合![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.函数![]() 在区间[0,
在区间[0,![]() ]上是 ( )
]上是 ( )
A.增函数 B.减函数 C.奇函数 D.偶函数
3.条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的( )
的( )
A.充分非必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要的条件
4.若函数![]() 满足
满足![]()
![]() ,则下列不恒成立的是( )
,则下列不恒成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和, 若
项和, 若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设![]() 是函数
是函数![]() 的反函数,若
的反函数,若![]() ,则
,则![]() 的值为( )
的值为( )
A. 1 B. 2 C. 3 D.![]()
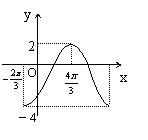 7.已知函数
7.已知函数![]() 的周期为T,在一个周期内
的周期为T,在一个周期内
的图象如图所示,则正确的结论是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.设数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 等于( )
等于( )
A.2005 B.-1003 C.-2005 D.1003
9.把曲线ycosx+2y-1=0先沿x轴向右平移![]() 个单位,再沿y轴向下平移1个单位,得到的曲线方程是( )
个单位,再沿y轴向下平移1个单位,得到的曲线方程是( )
A.(1-y)sinx+2y-3=0 B.(y-1)sinx+2y-3=0
C.(y+1)sinx+2y+1=0 D.-(y+1)sinx+2y+1=0
10.已知函数![]() ,若关于
,若关于![]() 的方程
的方程![]() 在区间
在区间
![]() 上有解,则
上有解,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
11.已知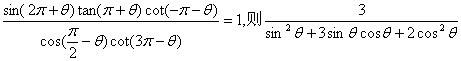 的值是
的值是
2/3 .
12.已知数列![]() 满足:
满足:![]() ,则使
,则使![]() 成立的
成立的![]() 的值是 21 .
的值是 21 .
13.函数![]() 的图象与直线
的图象与直线![]() 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则![]() 的取值范围是
的取值范围是![]() .
.
14.某俱乐部准备承办一场足球赛,预计卖出门票2.4万张,票价有3元、5元和8元三种,且票价3元和5元的张数的积为0.6万张。设x是门票的总收入,经预算,扣除其他各项开支后,该俱乐部的纯收入函数y=lg2x,则这三种门票分别为 0.6、1、0.8 万张时纯收入最大.
解:0.6; 1; 0.8设3元、5元、8元张数分别为a、b、c,则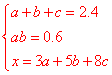
①代入③有![]()
时等号成立,由于y=lg2x为增函数,即此时y也有最大值.
三、解答题
15.已知集合A={xlog![]() (x-a2)<0},B={xx-3<a},若A∪B=A,求实数a的取值范围.
(x-a2)<0},B={xx-3<a},若A∪B=A,求实数a的取值范围.
解:对A,由log![]() (x-a2)<0知,
(x-a2)<0知,![]() x>a2+1,
x>a2+1,
所以A={x x>a2+1}------------------------------------------------------------------------------4分
由A∪B=A知B![]() A.
A.
对B,当a≤0时,B=![]() 符合题意.(*)-----------------------------------------------------6分
符合题意.(*)-----------------------------------------------------6分
当a>0时,B={x3-a<x<3+a}.-------------------------------------------------------------8分
而B![]() A,所以,a2+1≤3-a,
A,所以,a2+1≤3-a,
解之得-2≤a≤1,∴0<a≤1.------------------------------------------------------------------10分
综合(*)得,满足题意的a的取值范围是a≤1.---------------------------------------------12分
16.设![]() 是第二象限的角,
是第二象限的角,![]()
![]() ,求
,求![]() 的值.
的值.
解:∵![]() ,
,![]() 是第二象限角,∴
是第二象限角,∴![]()
![]() ,-----------------------------------------3分
,-----------------------------------------3分
![]()
![]()
![]()
![]() ---------------------------------------9分
---------------------------------------9分
故![]()
![]()
![]() .--------------------------------------------------------------------------------------12分
.--------------------------------------------------------------------------------------12分
17.已知向量
![]()
![]() 与
与![]() 为共线向量,且
为共线向量,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
解:(1)![]()
即![]() -----------------------------------------------------------------------------4分
-----------------------------------------------------------------------------4分
(2)![]() ---------------------------------- 8分
---------------------------------- 8分
![]()
![]() -------------------------------------------------------------------------------12分
-------------------------------------------------------------------------------12分
![]() --------------------------------------------------------------------------14分
--------------------------------------------------------------------------14分
18.设![]() 为等差数列,
为等差数列,![]() 为等比数列,
为等比数列,![]() 分别求出
分别求出![]() 及
及![]() 的前10项的和
的前10项的和![]()
解:设等差数列![]() 的公差为
的公差为![]() 等比数列
等比数列![]() 的公比为
的公比为![]() ------------------------------------1分
------------------------------------1分
![]() ①-----------------------------------3分
①-----------------------------------3分
又![]()
![]() ②-----------------------5分
②-----------------------5分
则由①,②得![]() ------------------------------------------------------------------------------7分
------------------------------------------------------------------------------7分
![]() ------------------------------------------------------------------9分
------------------------------------------------------------------9分
将![]() 代入①,得
代入①,得![]() ------------------------------------------------11分
------------------------------------------------11分
当![]() 时,
时,![]() --------------------------------------------------------------13分
--------------------------------------------------------------13分
当![]() 时,
时,![]() -----------------------------------------------------------14分
-----------------------------------------------------------14分
19.已知函数f(x)=为R上的奇函数.
⑴求f(x)及f-1(x)的解析式;
⑵若当x∈(-1,1)时,不等式f-1(x)≥log2恒成立,试求m的取值范围.
解:⑴∵f(x)=是奇函数,∴f(x)+f(-x)=0,--------------------------------------------2分
即+=+==a-1=0,∴a=1--------5分
∴f(x)=------------------------------------------------------------------------------------------6分
设y=,则(2x+1)y=2x-1,∴2x=,x=log2.令>0得-1<y<1,
∴f(x)的反函数为y=f-1(x)=log2.---------------------------------------9分
⑵∵当x∈(-1,1)时,f-1(x)≥log2恒成立,即log2≥log2,
∴≥.--------------------------------------------------------------------------------------11分
∵x∈(-1,1),∴1+x>0,1-x>0,m>0,
∴m≥1-x,当x∈(-1,1)时,1-x的取值集合为(0,2),∴m≥2.-------------------14分
20.已知一次函数![]() 的反函数为
的反函数为![]() ,且
,且![]() ,若点
,若点![]() 在曲线
在曲线![]() 上,
上,![]() ,对于大于或等于2的任意自然数
,对于大于或等于2的任意自然数![]() 均有
均有 ![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)求![]() 的通项公式;
的通项公式;
(3)设![]() ,求
,求![]()
解:(1)∵![]() 为一次函数,且
为一次函数,且![]() 为其反函数,
为其反函数,
∴设![]() 。
。
由![]() 得,
得,![]() ,即
,即![]()
![]() 且
且![]() 均在其上,
均在其上,
∴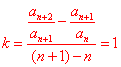 ,∴
,∴![]() 。------------------------------------------------------
6分
。------------------------------------------------------
6分
(2)由![]() 得:
得:
当![]() 时,
时,![]() ,
,
又∵![]() ,∴
,∴![]() ------------------------------------------------------------------------------10分
------------------------------------------------------------------------------10分
(3)![]()
![]()
![]()
![]() ,--------------------------------------------------------------------------------------12分
,--------------------------------------------------------------------------------------12分
![]() 。---------------------------------------------------------------14分
。---------------------------------------------------------------14分