河南省实验中学2005高三数学月考试题

河南省实验中学2005—2006学年度高三年级月考试题

 数学试卷（文科）

YCY本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.

第I卷（选择题，共60分）

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求。

1．设集合M={xx≤2+，x∈R}，N={1，2，3，4}，则M∩N=　　　　　　　　　　　　（　　）

　　　 A．{1，2}　　　　　　　 B．{1，2，3}　　　　　C．N　　　　　　　　　　　 D．M

2．点（0，1）到直线2x－y+2=0的距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　 C．　　　　　　　　　 D．

3．函数y=sinx－cosx, x∈R的最大值是　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．1　　　　　　　　　　　　C．　　　　　　　　　 D．0

4．曲线y=x³－x²－1在点（1，－1）处的切线的斜率是　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．－1　　　　　　　　　　 B．1　　　　　　　　　　　　C．－2　　　　　　　　　　 D．0

5．a、b是不相互垂直的异面直线，α、β是分别过a、b的平面，则下列四种情况：

　　　 ①α//β　　　　　　　　　 ②α⊥β　　　　　　　　　③a//β　　　　　　　　　　 ④a⊥β

　 其中可能出现的有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．1种　　　　　　　　　　B．2种　　　　　　　　　　C．3种　　　　　　　　　　D．4种

6．设α为第二象限角，且sin²α+sinαcosα－2cos²α=0, 则tanα=　　　　　　　　　　　 （　　）

　　　 A．1　　　　　　　　　　　　B．－1　　　　　　　　　　 C．2　　　　　　　　　　　　D．－2

7．函数f(x)=－x²+(a+1)x+2a的图象关于直线x=1对称，若f(x₁)=f(x₂)=0，则x₁－x₂=（　　）

　　　 A．4　　　　　　　　　　　　B．2　　　　　　　　　C．2　　　　　　　　　D．3

8．的展开式中的常数项为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．108　　　　　　　　　　 B．96　　　　　　　　　　　 C．72　　　　　　　　　　　D．84

9．函数f(x)是定义在R上的奇函数，当x≥0时，f(x)=(1+x)，则f(－2)=　　　（ 　 ）

　　　 A．－2　　　　　　　　　　 B．2　　　　　　　　　　　　C．－3　　　　　　　　　　 D．3

10．若三棱锥的顶点S在底面上的射影H恰好是底面三角形的三条高的交点，则三棱锥必有　　　　　　　　　　　　　　　　　 （　　）

　　　 A．三条侧棱长相等　　　　　　　　　　　　　　　　 B．三个侧面与底在所成的二面角相等

　　　 C．三条侧棱分别与它相对的棱垂直　　　　D．一定是正三棱锥

11．在数列{a_n}中，a₁=1,且a_n－a_n－1=n(n≥2；n∈N*)，则a_n=　　　　　　　　　　　　　　　　 （　　）

　　　 A．n²－n+1　　　　　　　B．n²+n－1　　　　　　　C．n²－n　　　　　D．n²+n

12．设O为坐标原点，A、B为抛物线y²=4x上两点，F为抛物线的焦点,∈R），

则=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．3λ　　　　　　　　　　 B．3　　　　　　　　　　　　C．－3λ　　　　　　　　 D．－3

第Ⅱ卷（非选择题，共90分）

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

13．设f(x)=2^1－x，则f^－1(8)=　　　　　　 

14．不等式的解集为　　　　　  

15．某单位要从A、B、C、D四个人中选出三人担任三种不同的职务，则上届任职的A、B、C三人都不连任原职的选法有　　　  种（用数字作答）

16．方程表示曲线C，有下列命题：

　　　 ①若1<t<4，则C为椭圆；　　　　　　　　　　　②若t<1或t>4，则C为双曲线；

　　　 ③C不可能为抛物线；　　　　　　　　　　　　　　 ④若1<t<，则C为长轴在x轴上的椭圆

　　其中真命题的序号有　　　　 （把你认为真命题的序号都填上）

三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。

17．（本小题满分12分）

设甲、乙两名同学投篮，甲投中的概率为0.7，乙投中的概率为0.8，两人是否投中相互之间没有影响.求：

（I）两人各投篮1次，只有1人投中的概率；

（II）每人各投篮2次，甲投中1次、乙投中2次的概率.

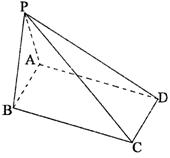
18．（本小题满分12分）

如图，四棱锥P—ABCD的底面是AB=2，BC=的矩形，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD.

（I）证明：侧面PAB⊥侧面PBC；

（II）求侧棱PC与底面ABCD所成的角；

（III）求直线AB与平面PCD的距离.

19．（本小题满分12分）

　 已知等比数列{a_n}中，a₁=3, a_n>0，n=1, 2……，a₂ +6是a₁与a₃的等差中项.

　（I）设b_n=2a_n+a_n+1, n=1, 2,……，求数列{b_n}的前n项和S­_n；

　（II）设C_n=n=1, 2,……，数列{C_n­}的前n项和为T_n，证明：T_­n<1.

20．（本小题满分12分）

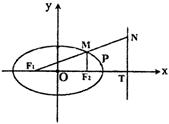
椭圆的右准线与x轴交于点T，过左焦点F₁作倾斜角为

30°的直线分别是交椭圆和右准线于M、N两点，且MF₂//NT（F₂为右焦点）.

（I）求椭圆离心率e；

（II）证明：F₁M=NT.

21．（本小题满分12分）

已知锐角三角形ABC中，

（I）求sin(A+B)的值；

（II）设m=(sinA, sinB), n=(cosB, －cosA), 且m·n=，求的值.

22．（本小题满分14分）

设a为正实数，函数f(x)=x³－ax²－a²x+1, x∈R.

（I）求f(x)的极值；

（II）设曲线y=f(x)与直线y=0至多有两个公共点，求实数a的取值范围.

数学试卷（文科）参考答案

一、选择题：

　　BAABC　 DCDAC　 DD

二、填空题

　 13．－2 ；　　14．；　15．11；　　　 16．②③④

三、解答题

17．解：（I）记“甲投篮1次投中”为事件A，“乙投篮1次投中”为事件B，则P（A）=0.7，P（B）=0.8，由题意，A、B是相互独立事件.

　　两人各投篮1次，只有1人投中的概率

　　…………（3分）

　　=0.7×(1－0.8)+(1－0.7)×0.8

　　=0.38……………………………………………………………………………………（5分）

（II）因为甲投篮2次，投中1次概率P₁=0.7×(1－0.7)=0.42……………………（7分）

　　 乙投篮2次，投中2次的概率P₂=0.8²=0.64…………………………………（9分）

　　 所以每人各投篮2次，甲投中1次、乙投中2次的概率

　　 P=P₁×P₂=0.42×0.64=0.2688……………………………………………………… （12分）

18．（I）证明：在矩形ABCD中，BC⊥AB

　　又∵面PAB⊥底面ABCD，侧面PAB∩底面ABCD=AB

　　∴BC⊥侧面PAB…………………………（2分）

　　又∵BC侧面PBC

　　∴侧面PAB⊥侧面PBC………………… （4分）

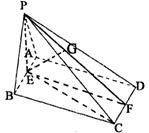
（II）解：取AB中点E，连结PE、CE

　　又∵△PAB是等边三角形

　　∴PE⊥AB

　　又∵侧面PAB⊥底面ABCD，∴PE⊥面ABCD

　　∴∠PCE为侧棱PC与底面ABCD所成角……………………………………………（6分）

　　

　　在Rt△PEC中，∠PCE=45°为所求…………………………………………（8分）

（Ⅲ）解：在矩形ABCD中，AB//CD

　　∵CD侧面PCD，AB侧面PCD，∴AB//侧面PCD

取CD中点F，连EF、PF，则EF⊥AB

又∵PE⊥AB　　∴AB⊥平面PEF

又∵AB//CD　　∴CD⊥平面PEF

∴平面PCD⊥平面PEF…………………………………………………………（10分）

作EG⊥PF，垂足为G，则EG⊥平面PCD

在Rt△PEF中，EG=为所求……………………………… （12分）

19．解：（I）设{a_n}的公比为q，则3q+6=

整理得q²－2q－3=0，解得q=3,或q=－1

∵a_n>0　, ∴q=3……………………………………………………………………3分

∴a_n=3ⁿ_.b_n=2×3ⁿ+3ⁿ⁺¹=15×3^n－1……………………………………………………5分

∴S_n=……………………………………………………7分

（II）………………………………………………………9分

　　 ∴…………………………11分

　　 ∵n∈N*　 ∴T_n<1………………………………………………………………12分

20．（I）∵NT//MF₂，NT⊥x轴，∴MF₂⊥x轴，……………………2分　

Rt△MF₁F₂中，∠MF₁F₂=30°。

设MF₂=2m，则MF₁=4m，

∴F₁F₂=2，m(m>0)

故2a=MF₁+MF₂=6m,

2c=F₁F₂=2m, ∴e=……6分　

（II）由（I）F₁（－m，0），则直线F₁N的方程为 y=(x+m)= x+m……9分

右准线方程x==3m，代入上式，得

y=4m　　∴NT=4m

又由（I）知F₁M=4m　∴F₁M=NT　 ……………………………………12分

21．解：（I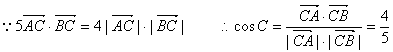）……（3分）

∴sinC=

sin(A+B)=sin(π－C)=sinC=………………………………………………6分

（II）m·n=sinAcosB－cosAsinB=　…………………………………………8分

sin(A+B)=sinAcosB+cosAsinB=　

由此得sinAcosB=　　  ①

　　　　　 cosAsinB=　②………………………………………………10分

①÷②得=2　　　 ……………………………………………………12分

22．（I）f′(x)=3x²－2ax－a²…………………………………………………………2分

由f′(x)=3x²－2ax－a²=0，得x₁=－，x₂=a, (a>0)

x	(－，－)	－	(－,a)	a	(a,+ ∞)
f′(x)	+	0	－	0	+
f(x)	增	极大	减	极小	增

……………………………………………………………………………………5分

∴f(x)_(极大)=f

f(x)_(极小)=f(a)=a³－a³－a³+1=1－a³……………………………………………………7分

（II）∵f(x)在（－∞，－）上递增，在（－,a）上递减，在(a,+ ∞)上递增，

f(x)_（极大）= a³+1>0………………………………………………………………9分

（1）当极小值f(a)=1－a³≥0，即0<a≤1时

y=f(x)与y=0在x∈（－，+∞）上有1个或0个公共点，此时f(－1)=a(a－1) ≤0

∴y=f(x)与y=0　在x∈（－∞，－）上有1个公共点

∴0<a≤1时，y=f(x)与y=0有1个或2个公共点…………………………………11分

（2）当极小值f(a)=1－a³<0即a>1时

y=f(x)与y=0在x∈（－，+∞）上有2个公共点，此时f(－a)=1－a³<0

∴y=f(x)与y=0 在x∈（－∞，－）上有1个公共点

∴a>1时，y=f(x)与y=0有3个公共点…………………………………………13分

综上，0<a≤1……………………………………………………………………14分