2005年潍坊市高三年级统一考试
数学试卷(理工农医类)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第I卷(选择题 共60分)
参考公式:
|
|
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.复数![]() 在复平面内的对应点位于 ( )
在复平面内的对应点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知向量![]() 的值为 ( )
的值为 ( )
A.1 B.![]() C.
C.![]() D.
D.![]()
4.已知函数![]() 和
和![]() ,其中
,其中![]() ,则它们反函数的图象关于 ( )
,则它们反函数的图象关于 ( )
A.x轴对称 B.y轴对称 C.直线![]() 对称 D.原点对称
对称 D.原点对称
5.函数![]() 是R上的偶函数,且在
是R上的偶函数,且在![]() 上是增函数,若
上是增函数,若![]() ,则实数a的取值范围是 ( )
,则实数a的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.等差数列![]() ,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是 ( )
,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-1
D.-1
7.设![]() 是三个不重合的平面,l是直线,给出下列命题
是三个不重合的平面,l是直线,给出下列命题
①若![]() ,则
,则![]() ; ②若l上两点到
; ②若l上两点到![]() 的距离相等,则
的距离相等,则![]() ;
;
③若![]() ④若
④若![]()
其中正确的命题是 ( )
A.①② B.②③ C.②④ D.③④
8.对某种产品的5件不同正品和4件不同次品一一进行检测,直到区分出所有次品为止. 若所有次品恰好经过五次检测被全部发现,则这样的检测方法有 ( )
A.20种 B.96种 C.480种 D.600种
9.棱长都为2的直平行六面体ABCD—A1B1C1D1中,∠BAD=60°,则对角线A1C与侧面DCC1D1所成角的正弦值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.椭圆![]() 的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则PF2的值等于 ( )
的左准线为l,左、右焦点分别为F1,F2,抛物线C2的准线为l,焦点是F2,C1与C2的一个交点为P,则PF2的值等于 ( )
A.![]() B.
B.![]() C.4 D.8
C.4 D.8
11.若函数![]() ,则函数
,则函数![]() 的图象与函数
的图象与函数![]() 的图象的交点个数为 ( )
的图象的交点个数为 ( )
A.2 B.3 C.4 D.无数个
12.如图,南北方向的公路l,A地在公路的正东2km处,
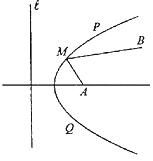 B地在A地东偏北30°方向2
B地在A地东偏北30°方向2![]() km处, 河流沿岸
km处, 河流沿岸
PQ(曲线) 上任一点到公路l和到A地距离相等.现
要在曲线PQ上选一处M建一座码头,向A、B两地
转运货物,经测算从M到A, M到B修建公路的费
用均为a万元/km,那么修建这两条公路的总费用最低
是 ( )
A.![]() 万元 B.
万元 B.![]() 万元
万元
C.5a万元 D.6a万元
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.如果把圆![]() 平移后得到圆C′,且C′与直线
平移后得到圆C′,且C′与直线![]() 相切,则m的值为 .
相切,则m的值为 .
14.等比数列![]() 中,已知
中,已知![]()
![]() =
.
=
.
15.锥体体积V可以由底面积S与高h求得:![]() . 已知正三棱锥P—ABC底面边长为2
. 已知正三棱锥P—ABC底面边长为2![]() ,体积为4
,体积为4![]() ,则底面三角形ABC的中心O到侧面PAB的距离为 .
,则底面三角形ABC的中心O到侧面PAB的距离为 .
16.若函数![]() 满足:
满足:
对于任意![]() 成立,则称函数
成立,则称函数![]() 具有性质M.
具有性质M.
给出下列四个函数:①![]() ,②
,②![]() ③
③![]() ,④
,④![]() .
.
其中具有性质M的函数是 .
(注:把满足题意的所有函数的序号都填上)
三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
| 排队人数 | 0—5 | 6—10 | 11—15 | 16—20 | 21—25 | 25人以上 |
| 概 率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(I)每天不超过20人排队结算的概率是多少?
(Ⅱ)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
18.(本小题满分12分)
正四棱柱ABCD—A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,
![]() .
.
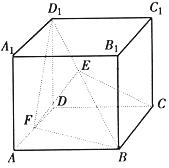
(I)建立适当的坐标系,求出E点的坐标;
(Ⅱ)证明:EF是异面直线D1B与AD的公垂线;
(Ⅲ)求二面角D1—BF—C的余弦值.
19.(本小题满分12分)
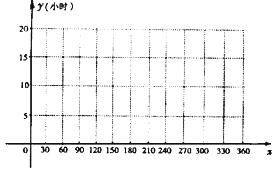
下表是某地一年中10天测量的白昼时间统计表(时间近似到0.1小时)
| 日期 | 1月1日 | 2月28 日 | 3月21 日 | 4月27 日 | 5月6 日 | 6月21 日 | 8月13 日 | 9月20 日 | 10月25日 | 12月21日 |
| 日期位置序号x | 1 | 59 | 80 | 117 | 126 | 172 | 225 | 263 | 298 | 355 |
| 白昼时间y(小时) | 5.6 | 10.2 | 12.4 | 16.4 | 17.3 | 19.4 | 16.4 | 12.4 | 8.5 | 5.4 |
(I)以日期在365天中的位置序号x为横坐标,白昼时间y为纵坐标,在给定坐标系中画出这些数据的散点图;
(Ⅱ)试选用一个形如![]() 的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
(Ⅲ)用(Ⅱ)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
20.(本小题满分12分)
设函数![]() R.
R.
(I)求函数![]() 的最值;
的最值;
(Ⅱ)给出定理:如果函数![]() 在区间[
在区间[![]() ]上连续,并且有
]上连续,并且有![]() ,那么,函数
,那么,函数![]() 在区间
在区间![]() 内有零点,即存在
内有零点,即存在![]() .
.
运用上述定理判断,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内是否存在零点.
内是否存在零点.
21.(本小题满分12分)
双曲线![]() 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为![]() ,其中A(0,-b),B(a,0).
,其中A(0,-b),B(a,0).
(I)求双曲线的标准方程;
(Ⅱ)设F是双曲线的右焦点,直线l过点F且与双曲线的右支交于不同的两点P、Q,点M为线段PQ的中点. 若点M在直线![]() 上的射影为N,满足
上的射影为N,满足![]()
且![]() ,求直线l的方程.
,求直线l的方程.
22.(本小题满分14分)
设![]() 的图象上任意两点,且
的图象上任意两点,且![]() ,已知点M的横坐标为
,已知点M的横坐标为![]() .
.
(I)求证:M点的纵坐标为定值;
(Ⅱ)若![]() ;
;
(Ⅲ)已知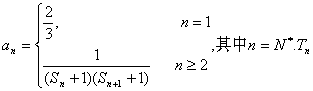 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 都成立,试求
都成立,试求![]() 的取值范围.
的取值范围.
数学试卷(理工农医类)参考答案及评分标准
一、选择题:本题考查基本知识和基本运算,每小题5分,满分60分.
ADAAD BDCCB CC
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分.
13.![]() 14.
14.![]() 15.
15.![]() 16.①③
16.①③
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
解:(I)每天不超过20人排队结算的概率为:P=0.1+0.15+0.25+0.25=0.75,即不超过20
人排队结算的概率是0.75. ……………………4分
(Ⅱ)每天超过15人排队结算的概率为:
0.25+0.2+0.05=![]() , ……………………6分
, ……………………6分
一周7天中,没有出现超过15人排队结算的概率为![]() ;
;
一周7天中,有一天出现超过15人排队结算的概率为![]() ;
;
一周7天中,有二天出现超过15人排队结算的概率为![]() ;……………9分
;……………9分
所以有3天或3天以上出现超过15人排队结算的概率为:
![]() ,
,
所以,该商场需要增加结算窗口. ……………………12分
18.(本小题满分12分)
解:(I)以D为原点,DA,DC,DD1所在直线为x轴,y轴,z轴,建立空间直角坐标系,则A、B、C的坐标分别为A(2,0,0)、B(2,2,0)、C(0,2,0).
设D1(0,0,2m)(m>0),则E(1, 1, m).
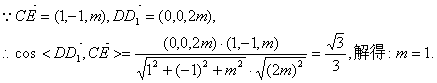
故E点坐标为(1,1,1). ……………………4分
(Ⅱ)由(I)可知,正四棱柱ABCD—A1B1C1D1是棱长为2的正方体.
又∵FD=1, ∴F(1,0,0),
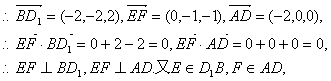
故EF是AD与D1B的公垂线. ……………………8分
(Ⅲ)设n⊥平面FD1B,n=(x,y,z)
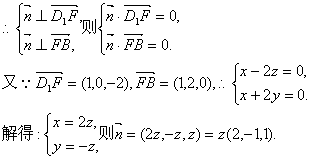
取n0=(2,-1,1), ……………………10分
则n0与![]() 所成角θ等于二面角D1—FB—C的平面角,
所成角θ等于二面角D1—FB—C的平面角,
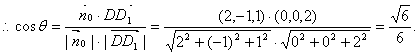
∴二面角D1—BF—C的余弦值为![]() ……………………12分
……………………12分
解法二:(Ⅲ)延长CD交BF延长线于P,
作DN⊥BP于N,连ND1,
∵DD1⊥平面ABCD,∴ND1⊥BP,∴∠DND1就是二面角D1—FD—C的平面角.
……………………10分
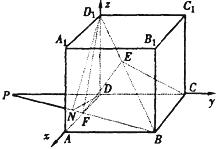 在Rt△DFP中,DP=2,FD=1,FP=
在Rt△DFP中,DP=2,FD=1,FP=![]() ,
,
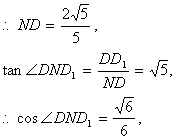
∴二面角D1—BF—C的余弦值为![]() . ……………………12分
. ……………………12分
19.(本小题满分12分)
(I)画散点图见下面.
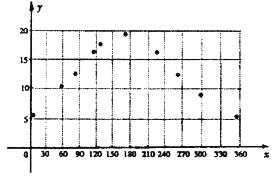 ……………………4分
……………………4分
(Ⅱ)由散点图知白昼时间与日期序号之间的函数关系近似为
![]() ,
,
由图形知函数的最大值为19.4,最小值为5.4,
即![]() ,
,
由19.4-5.4=14,得A=7;
由19.4+5.4=24.8,得t=12.4;
又T=365,![]() ……………………7分
……………………7分
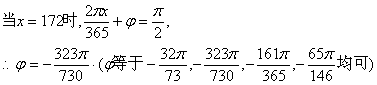
![]() ……………………9分
……………………9分
(Ⅲ)![]()
![]() ……………………11分
……………………11分
∴该地大约有121天(或122天)白昼时间大于15.9小时. ……………………12分
20.(本小题满分12分)
解:(I)![]()
令![]() ……………………2分
……………………2分
|
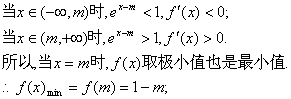
由①知f(x)无最大值. ……………………6分
(Ⅱ)函数f(x)在[m,2m]上连续.
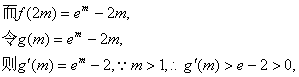
![]() 上递增. ……………………8分
上递增. ……………………8分
由![]() ……………………10分
……………………10分
又![]()
根据定理,可判断函数f(x)在区间(m,2m)上存在零点. ……………………12分
21.(本小题满分12分)
解:(I)依题意有: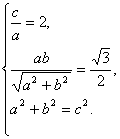 ……………………2分
……………………2分
解得:![]()
所以,所求双曲线的方程为![]() ……………………4分
……………………4分
(II)(法1)当直线![]() 轴时,
轴时,![]() ,不合题意.
,不合题意.
当直线l的斜率存在时,设直线l的方程为![]() .
.
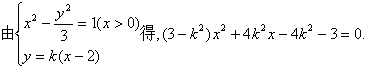 ①………………6分
①………………6分
因为直线与双曲线的右支交于不同两点,所以![]()
设![]() 是方程①的两个正根,于是有
是方程①的两个正根,于是有
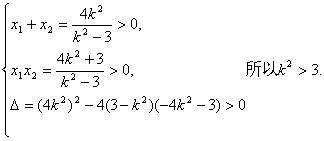 ②…………………8分
②…………………8分
因为![]()
所以PM=MN=MQ=![]() PQ=5.
PQ=5.
又MN=x0+2=5,即x0=3, ……………………10分
而![]() .
.
![]() ②式,
②式,![]() 符合题意.
符合题意.
所以直线l的方程为:![]() (x-2). ……………………12分
(x-2). ……………………12分
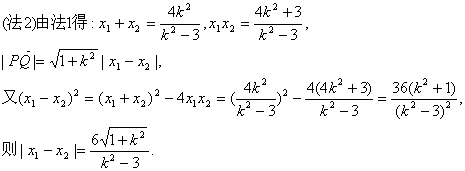
又![]() . ……………………9分
. ……………………9分
显然k=±3满足②式.
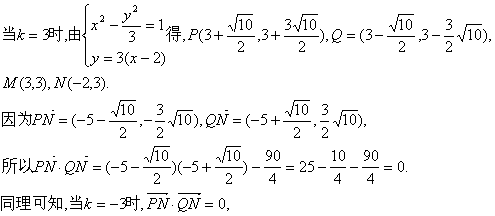
所以所求直线的方程为![]() . ……………………12分
. ……………………12分
22.(本小题满分14分)
(I)证明:![]() M是AB的中点,设M点的坐标为(x,y)
M是AB的中点,设M点的坐标为(x,y)
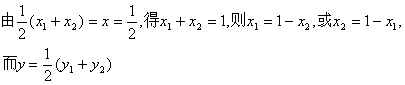
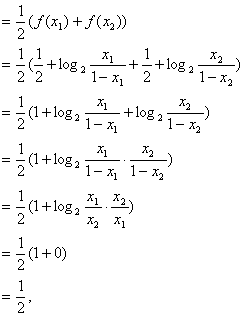
∴M点的纵坐标为定值![]() . ……………………4分
. ……………………4分
(II)解:由(I)知![]()
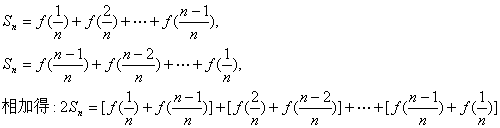
![]() ……………………8分
……………………8分
![]() . ……………………9分
. ……………………9分
(III)![]()
![]()
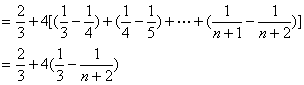
![]() ……………………11分
……………………11分

因此![]() ……………………14分
……………………14分