高三年三校联考数学(理)试卷
一、选择题:(每小题5分,共60分)
1、设i为虚数单位,![]() 的值为 ( )
的值为 ( )
A、-1+i B、-1-i C、1+ i D、1- i
2.![]() (
)
(
)
A.1 B![]()
![]() C
C![]()
![]() D
D![]() 不存在 3.
不存在 3.![]() (
)
(
)
A、4 B、8 C、0 D、2
4、直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A、3 B、-3 C、5 D、-5
5、若不等式![]() 的解集为
的解集为![]() ,则实数
,则实数![]() 等于( )
等于( )
A、8 B、2 C、-4 D、-8
6、设抛物线![]() 的准线为l,将圆
的准线为l,将圆![]() 按向量
按向量![]() 平移后恰与l相切,则p的值 ( )
平移后恰与l相切,则p的值 ( )
A、![]() B、2
C、4
D、
B、2
C、4
D、![]() C
C
7、如果以原点为圆心的圆经过双曲线![]() 的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于 ( )
的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、已知椭圆![]() 的焦点
的焦点![]() 、
、![]() ,椭圆上一点
,椭圆上一点![]() 有
有![]() ,则
,则![]() 的面积为 ( )
的面积为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、棱长为![]() 的正四面体内接于球,则球的表面积(
)
的正四面体内接于球,则球的表面积(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、如果f(a+b)=f(a)•f(b)且f(1)=2,则![]()
![]() +
+![]() +
+![]() +…+
+…+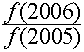 等于(
)
等于(
)
A、2005 B、1002 C、2006 D、1003
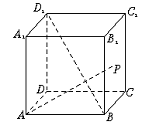 11、如图,正方体ABCD—A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则动点P的轨迹是( )
11、如图,正方体ABCD—A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则动点P的轨迹是( )
A.线段B1C B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段.
12、下面四个命题:
①
“![]() ”的充要条件是“
”的充要条件是“![]() 所在“平面””
所在“平面””
②
“直线![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() ”
”
③ “直线a、b为异面直线”的充分不必要条件是“a、b不相交”
④ “平面![]() 平面
平面![]() ”的必要不充分条件是“平面
”的必要不充分条件是“平面![]() 内存在不等线三点到平面
内存在不等线三点到平面![]() 的距离相等”
的距离相等”
其中正确命题的序号是:( )
A、①② B、②③ C、③④ D、②④
二、填空题 (每小题4分,共16分)
13、已知向量![]() =(k,12),
=(k,12),![]() =(4,5),
=(4,5),![]() =(-k,10),且A、B、C三点共线,则k=______.
=(-k,10),且A、B、C三点共线,则k=______.
14、设实数![]() 满足约束条件
满足约束条件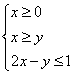 则
则![]() 的最大值
的最大值
15.已知A (![]() ,0 ),B是圆
,0 ),B是圆![]() 为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.
为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.
16、直线![]() ,
,![]() 与
与 ![]() 轴,
轴,![]() 轴的正半轴围成的四边形有外接圆,则k=
轴的正半轴围成的四边形有外接圆,则k=
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或推演步骤。
17![]() 已知
已知![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围
的取值范围![]()
18、已知点 A(2,0),B(0,2),C(cos![]() ,sin
,sin![]() ),且0<
),且0<![]() <
<![]()
(I) 若![]() +
+![]() =
=![]() ,求
,求![]() 与
与![]() 的夹角;
的夹角;
(II)若![]() ⊥
⊥![]() ,求tan
,求tan![]() 的值。
的值。
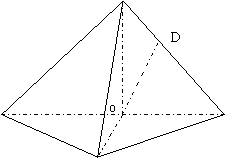
19、如图:在三棱锥P—ABC中,![]()
![]() =m,点O、D分别为AC、PC中点,OP上底面ABC
=m,点O、D分别为AC、PC中点,OP上底面ABC
(1)求证:![]() 平面PAB
平面PAB
(2)当![]() 时,求直线PA与平面PBC所成角的大小
时,求直线PA与平面PBC所成角的大小
(3)当m取何值时,O在平面PBC内的射影恰好为![]() 的重心。
的重心。
|
|
|
|

20..、已知函数f(x)=ax2+bx+1(a,b∈R)
(1)若 f(-1)=0,且对任意实数x均有f(x) ≥0成立,求f(x)表达式
(2)在(1)条件下,当x∈[-2,2]时,S(x)=xf(x)-kx单调递增,求实数k取值范围.
21、已知数列{an}的前n项和为Sn,又有数列{bn},它们满足关系b1=a1,对n∈N+,有an=n-Sn , bn+1=an+1-an.
(1)求{bn}通项公式
(2)求![]()
(3)若令Cn= ![]() ,求满足C1+C2+…+Cn<400的最大的正整数n.
,求满足C1+C2+…+Cn<400的最大的正整数n.
22、已知定点R的坐标为(0,-3),点P在x轴上,![]() ⊥
⊥![]() ,线段PM与y轴交于点Q,且满足
,线段PM与y轴交于点Q,且满足![]() =2
=2![]()
(1) 若点P在x轴上运动,求点M的轨迹E;
(2) 求轨迹E的倾斜角为![]() 的切线
的切线![]() 0的方程;
0的方程;
(3) 若(2)中切线![]() 0与y轴交于点G,过G的直线
0与y轴交于点G,过G的直线![]() 与轨迹E交于A、B两点,点D的坐标为 (0,1),当∠ADB为钝角时,求直线
与轨迹E交于A、B两点,点D的坐标为 (0,1),当∠ADB为钝角时,求直线![]() 的斜率的取值范围。
的斜率的取值范围。
参考答案:
一:BBAAC CDAAC AD
二:13、-![]() 14、2 15、
14、2 15、![]() 16、3
16、3
三: 17![]() (本小题满分12分)
(本小题满分12分)
解:由![]() 得
得 ![]() 即1<x<2
即1<x<2
∴![]() ,
3分
,
3分
由![]() 得
得![]()
∴![]() 6分
6分
![]() 10分
10分
![]() 12分
12分
18、(12分)解:(I) ∵![]() =
=![]() ,即(2+cos
,即(2+cos![]() )2+sin2
)2+sin2![]() =7 ∴cos
=7 ∴cos![]() =
=![]()
又![]() ∈(0,
∈(0,![]() ) ∴
) ∴![]() =∠AOC=
=∠AOC=![]()
又∠AOB=![]() ∴
∴![]() 与
与![]() 的夹角为
的夹角为![]() 5分
5分
(II)![]() =(cos
=(cos![]() -2,sin
-2,sin![]() ),
),![]() =(cos
=(cos![]() , sin
, sin![]() -2)
-2)
又∵![]() ⊥
⊥![]() ∴
∴![]() ·
·![]() =0
=0
∴cos![]() +sin
+sin![]() =
=![]() …………………………① 8分
…………………………① 8分
∴2sin![]() cos
cos![]() =-
=-![]() ∵
∵![]() ∈(0,
∈(0,![]() ) ∴
) ∴![]() ∈(
∈(![]() ,
,![]() )
)
又由 (cos![]() -sin
-sin![]() )2=1-2sin
)2=1-2sin![]() cos
cos![]() =
=![]() 及cos
及cos![]() -sin
-sin![]() <0
<0
是cos![]() -sin
-sin![]() =-
=-![]() ……………………② 10分
……………………② 10分
由①、②的cos![]() =
=![]() ,sin
,sin![]() =
=![]() ∴tan
∴tan![]() =-
=-![]() 12
12
19(12分)解:(1)∵O、D分别为AC、PC的中点,∴OD∥PA。
又PA![]() 平面PAB,∴OD∥平面PAB。
4分
平面PAB,∴OD∥平面PAB。
4分
(2)∵AB⊥BC,OA=OC,∴OA=OB=OC,又OP⊥平面ABC,
∴PA=PB=PC。取BC中点E,连结PE,则BC⊥平面POE。作OF⊥PE于F,连结DF,则OF⊥平面PBC,∴∠ODF是OD与平面PBC所成的角。
又OD∥PA,∴PA与平面PBC所成的角的大小等于∠ODF。
在直角⊿ODF中,sin∠ODF=![]() =
=![]()
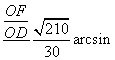 ∴PA与平面PBC所成的角为
∴PA与平面PBC所成的角为![]()
![]() 。 8分
。 8分
(3) 由(2)知,OP⊥平面ABC,![]() ∴F是O在平面ABC内的射影。
∴F是O在平面ABC内的射影。
∵D是PC的中点,若点F是⊿PBC的重心,则B、F、D三点共线,∴直线OB在平面PBC内的射影为直线BD。
∵OB⊥PC,![]() ∴PC⊥BD, PB=PC,即m=1.
∴PC⊥BD, PB=PC,即m=1.
反之,当m=1时,三棱锥O—PBC为正三棱锥,∴O在平面PBC内的射影为⊿PBC的重心。 12分
解法2:建立空间直角坐标系亦同样得分。
20(12分)解:(1)∵任意,x∈R,均有f(x)≥0,而f(-1)=0
∴a>0,且f(x)=a(x+1)2
从而ax2+bx+1=a(x+1)2得:b=2a且a=1
∴f(x)=x2+2x+1 6分
(2)依题意,当x∈[-2,2]时,g(x)=x3+2x2+x-kx为增函数
∴g(x)=3x2+4x+1-k≥0
即k≤3(x+![]() )2-
)2-![]()
∵3(x+![]() )2-
)2-![]() ≥-
≥-![]() 在[-2,2]恒成立.
在[-2,2]恒成立.
∴k≤-![]() 12分
12分
21、(12分)(1)当n≥2时,Sn=n-an,Sn—1=(n-1)-an—1
∴an=Sn-Sn—1=1+an—1-an 2
∴2(an-1)=an—1-1 即![]() =
=![]() 而a1=1-S1
而a1=1-S1![]() a1=
a1=![]() 4
4
∴数列{an-1}是以a1-1=-![]() 为首项,以
为首项,以![]() 为公比的等比数列
为公比的等比数列
∴![]() =1-
=1-![]() ,从而bn+1=an+1-an=
,从而bn+1=an+1-an=![]() -
-![]() =
=![]() 6 分
6 分
(2)![]() an=
an=![]() (1-
(1-![]() )=1
8 分
)=1
8 分
(3)Cn=2n-1 ∴C1+C2+…+Cn
=(2+22+…+2n)-n
=2n+1-2-n 10分
∴2n+1-2-n<400 故n=7 12 分
22、(14分)解:(1) 设点M的坐标为 (x, y),点P的坐标为 (x1,0),点Q的坐标为
(0,y2) (x1≠0),则![]() =(-x1,-3),
=(-x1,-3),![]() =(x-x1,y),
=(x-x1,y),![]() =(-x1,y2)
=(-x1,y2)
∵![]() ⊥
⊥![]() ∴
∴![]() ·
·![]() =0 ∴-x1(x-x1)-3y=0
=0 ∴-x1(x-x1)-3y=0
即x12-x1x-3y=0 由![]() =2
=2![]() 得
得![]() =
=![]()
![]()
∴x1=-![]() 代入上式的y=
代入上式的y=![]() x2 (x≠0)
6分
x2 (x≠0)
6分
(2) 设切点为 (x0, y0) ∵y1=![]() x ∴切线
x ∴切线![]() 0=
0=![]() x0=tan
x0=tan![]() =1
=1
∴x0=2 切点为 (2,1) ∴切线![]() 0的方程为x-y-1=0 8分
0的方程为x-y-1=0 8分
(3) ∵![]() 0的切线方程为x-y-1=0
∴G (0, -1)
0的切线方程为x-y-1=0
∴G (0, -1)
设![]() 的斜率为k
∴
的斜率为k
∴![]() 的方程为y=kx-1
的方程为y=kx-1
由 的x2-4k
的x2-4k![]() +4=0…………①
+4=0…………①
设A(x1, y1),B(x2, y2),则x1, x2是方程①的两根
∴△=16k2-16 >0 ∴k2>1 10分
∵∠ADB为钝角
∴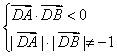
而![]() =(x1;y1-1),
=(x1;y1-1),![]() =(x2, y2-1)
=(x2, y2-1)
∴x1·x2+(y1-1) (y2-1)<0 ∴x1x2+(k x1-2) (kx2-2) <0
∴x1x2+k2 x1x2-2k(x1+x2)+4<0即k2-2>0 ∴k<-![]() 或k>
或k>![]() 14分
14分