华中师大一附中2005—2006学年度第一学期高三年级数学（理）期中试题
总分:150分 时间:120分钟
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。请把答案填在答题卡上。
1．与命题“若
，则
”等价的命题是
A．若，则
B．若，则
C．若
，则 D．若，则
2．命题
、
为简单命题，则“且”为真是“或”为真的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
3．函数
的定义域为
A．
，
B．,
, C．，
D．
，
4．已知
、
、
是三角形的三个顶点，
，则
为
A．等腰三角形 B．直角三角开
C．等腰直角三角形 D．既非等腰三角形又非直角三角形
5．集合
，
，
，
，
，
，则满足上述条件的集合、有
A．3对 B．4对 C．6对 D．8对
6．
、
，
、
、
是共起点的向量，、不共线，
，则、、的终点共线的充分必要条件是
A．
B．
C．
D．
7．关于函数
，有以下三种说法：
①图象的对称中心是点
，
②图象的对称轴是直线
③函数的最小正周期是
其中正确的说法是：
A．①②③ B．②③ C．①③ D．③
8．设
是以3为周期的周期函数，且
，
时
，
是
图象上的动点，
，
，则以
点的轨迹为图象的函数在
，
上的解析式为
A．
，
， B．
，，
C．
，， D．
，，
9．已知
，
，则
A．
B．
C．
D．
10．函数
在区间
，
上的值域为[0，1]，则
的最小值为
A．2 B．1 C．
D．
11．已知连续函数是
上的增函数，且点
，
、
，
在它的图象上，
为它的反函数，则不等式
的解集是
A．， B．
，
C．， D．，
12．某地2000年底，人口为500万，人均住房面积为6平方米，如果该地的人口年平均增长率为1%，为使该地到2010年底，人均住房面积达到7平方米，那么平均每年比上一年应新增住房面积（精确到0.1万平方米，已知
）
A．86.8万平方米 B．19.3万平方米
C．15.8万平方米 D．17.3万平方米
华中师大一附中2005—2006学年度第一学期
高二年级数学（理）期中试题答题卷
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分。请把答案填在题中横线上。
13．利用指数函数在同一坐标系中的图象比较大小可得
_____
。
14．在直角坐标平面内，已知点列
，、
，
、
，
，…，
，
，……如果
为正偶数，则向量
的坐标（用表示）为________。
15．已知数列
中，
，
时
，则的通项公式
。
16．已知是定义在实数集上的函数，且
，若
，则
=____________
三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。
17．（本小题满分12分）已知函数、
对任意实数
、
分别满足
①
且
；②
且
，
为正整数
（1）求数列
、
的通项公式；
（2）设
，求数列
的前项和。
18．（本小题满分12分）已知函数
，
，
，
(1)求函数的单调递增区间；
(2)当
时，写出由函数
的图象变换到与的图象重叠的变换过程。
19．（本小题满分12分）已知的三边
、、成等比数列，且
，
。
（1）求
； （2）求的面积。
20．（本小题满分12分）已知定义域为[0，1]的函数同时满足以下三条：①对任意的
[0，1]，总有
；②
；③若
，
，
，则有
成立。解答下列各题：
（1）求
的值；
（2）函数
在区间[0，1]上是否同时适合①②③？并予以证明；
（3）假定存在
[0，1]，使得
[0，1]且
，求证
。
21．（本小题满分14分）
已知向量
，
，
，
且
，
，
（1）用表示
；
（2）当最小时，求向量
与向量
的夹角
。
22．（本小题满分12分）设是定义在上的奇函数，且函数与
的图象关于直线
对称，当
时，
为常数）
（1）求的解析式；
（2）若对区间
，
上的每个值，恒有
成立，求的取值范围。
高三年级数学（理）期中参考答案
一、DACBBD DABDBC
二、13．
14．
，
15．
16．
三、17．（1）由
，
，知
成等比数列，
……………………………………………………3分
由②中令
，
，得
，知
成等差数列，
，即
……………………6分
（2）
………………………………………9分
……………………12分
18．
，， ……………………………4分
（1）
当
时，由
得单调增区间为
，………6分
同理，当
时，函数的单调递增区间为
，
……………8分
注：单调区间写成开区间，半开区间均给全分。
（2）当时，
，，
将
的图象右移
个单位可得
的图象，
再将图象上每个点的纵坐标扩大到原来的
倍，而横坐标保持不变，
可得
的图象，再将所得图象上移一个单位，可得
的图象。……………………………………12分
19．（1）由
，
………………………………………5分
由、
、成等比数列，知
，且不是最大边
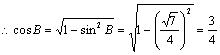…………………………………6分
（2）由余弦定理 
得
得
…………………………………………………………………11分
………………………………………………12分
20．（1）取
得
又由①
，故
…………………………………………4分
（2）显然，在[0，1]满足①
；满足②
若
，，
，则
故
适合①②③……………………………………………………8分
（3）由③知任给、
[0，1]，
时
事实上
、[0，1]，知
[0，1]
……………………10分
若
，则
前后矛盾
若
，则
前后矛盾
故
………………………………………………………12分
21．（1）
得 
………………………………………………4分
由
及
得
，
，
……………………………6分
令
，则
，
代入上式可得
当且仅当
，即
时，取“=”，
…………………10分
（2）此时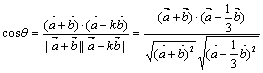 
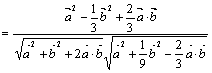………………………12分
将
，
，
代入上式可得
，
即
与的夹角为
…………………………………14分
22．（1）1°当
时，
，
设
，
为
上的任一点，则它关于直线
的对称点为
，
，满足 
且，适合
的表达式
即
……………………………4分
2°当
时，
，
为奇函数
………………………5分
3°当
时，
综上 
，
………………………………………6分
（2）由题意
，
时，
，
当
时，
恒成立，
在
，是增函数
得
，即
…………………………8分
当
时，令
得
，
若
，即
时，则
在，大于零，在，是增函数，得…………………………………10分
若
，即
时，则在，的最小值是
令
得
…………………………………………11分
综上 
………………………………………………………12分