湖北省武汉市2005—2006学年上学期高三年级调研测试
数 学 试 卷
YCY
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 满分150分.考试时间120分钟.
第Ⅰ卷(选择题,共60分)
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]()
球的表面积公式 ![]() 其中R表示球的半径
其中R表示球的半径
球的体积公式 ![]() 其中R表示球的半径
其中R表示球的半径
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知向量![]() 和
和![]() 不共线,且
不共线,且![]() =3,
=3,![]() =4,又向量
=4,又向量![]() +k
+k![]() 与
与![]() -k
-k![]() 互相垂直,则实数k
互相垂直,则实数k
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 的定义域是 ( )
的定义域是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.(文科)已知![]() ,则
,则![]() 的值是 ( )
的值是 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
(理科)设锐角![]() 满足
满足![]() ,则cos
,则cos![]() 值是 ( )
值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若不等式![]() 的解集为(-1,2),则实数a等于 ( )
的解集为(-1,2),则实数a等于 ( )
A.-4 B.4 C.-8 D.8
5.已知数列{![]() 前n项和
前n项和![]() 那么{
那么{![]() 是 ( )
是 ( )
A.一定是等比数列 B.一定是等差数列
C.或是等差数列或是等比数列 D.既非等差数列又非等比数列
6.若直线![]() 和直线
和直线![]() 关于直线
关于直线![]() 对称,那么直线
对称,那么直线![]() 恒过定点( )
恒过定点( )
A.(2,0) B.(1,-1) C.(1,1) D.(-2,0)
7.三棱锥P—ABC中,△ABC为等边三角形,PA⊥面ABC,PA=AB,则二面角A—PB—C
的平面角的正切值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.经过点M(0,2)且和x轴相切的面积最小圆为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.以正方体的顶点为顶点的三棱锥的个数是 ( )
A.![]() B.
B.![]() C.
C.![]() -6 D.
-6 D.![]() -12
-12
10.已知点P是双曲线![]() 上的点,且点P到双曲线右准线的距离是P到两个焦点距离的等差中项,则P点横坐标x为 ( )
上的点,且点P到双曲线右准线的距离是P到两个焦点距离的等差中项,则P点横坐标x为 ( )
A.![]() B.
B.![]() C.-
C.-![]() D.
D.![]()
11.(文)袋中有1个白球和4个黑球,每次从其中任取一个球,而且每次取出黑球后放回
袋中,则直到第三次取球时才取到白球的概率 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理)袋中有1个白球和4个黑球,每次从其中任取一个球,当每次取到黑球时不再放
回,直到取到白球为止,则取到球次数的数学期望为 ( )
A.5 B.2 C.3 D.4
12.函数![]() 的值域是 ( )
的值域是 ( )
A.![]() B.
B.![]() C.R D.
C.R D.![]()
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上.
13.在半径为13的球面上有A、B、C三点,AB=6,BC=8,CA=10,则球心到平面ABC的距离为 .
14.在条件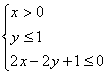 下,目标函数S=2x+y的最大值为
.
下,目标函数S=2x+y的最大值为
.
15.若![]() 的展开式中含
的展开式中含![]() 项,则最小自然数n是
.
项,则最小自然数n是
.
16.已知双曲线的对称轴与双曲线的交点即为双曲线的顶点,则双曲线![]()
的实轴长为 .
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知n为正整数,规定![]()
已知![]()
(1)解不等式![]() ;
;
(2)设集合A={0,1,2},对任意![]() ,证明:
,证明:![]()
18.(本小题满分12分)
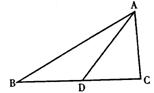
在△ABC中,![]() ,又D在线段BC上,且满足
,又D在线段BC上,且满足![]()
|
(2)若![]() 和
和![]() 夹角为60°,试用
夹角为60°,试用![]() ,
,![]() 及
及![]() 来表示
来表示![]()
19.(本小题满分12分)
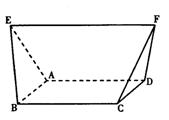
如图,几何体的底面ABCD是边长为a的正方形,EF∥面AC,EF=2a,
又AE=BE=CF=DF=a.
|
(2)求几何体EF—ABCD体积;
(3)(理科)求BF和底面ABCD所成角的正切值.
20.(本小题满分12分)
已知某人射击一次命中目标的概率是![]() 求:
求:
(1)此人射击6次恰好3次命中目标的概率;
(2)(文科)此人射击6次,3次命中且恰有两次连续命中的概率;
(3)(理科)此人射击6次,三次命中且不连续命中的概率.
21.(本小题满分12分)
(文科)已知数列![]() ,前n项和为Sn,对于任意的
,前n项和为Sn,对于任意的![]() 恒为等差数列.
恒为等差数列.
(1)求![]() ;
;
(2)证明:在![]() 时,数列
时,数列![]() 为等比数列.
为等比数列.
(理科)已知正项数列![]() 满足
满足![]() ,且
,且![]() 又
又![]() ,
,
![]() 求证:
求证:
(1)![]() ;
;
(2)![]()
22.(本小题满分14分)
|
(1)用![]() 来表示双曲线离心率e的值;
来表示双曲线离心率e的值;
(2)求![]() 的取值范围.
的取值范围.
湖北省武汉市2005—2006学年上学期高三年级调研测试
数学试卷参考答案
一、选择题:
1.C 2.D 3.(文)B,(理)D 4.A 5.C 6.C 7.B 8.A 9.D
10.C 11.(文)B,(理)C 12.B
二、填空题:
13.12 14.2 15.7 16.4![]()
三、解答题:
17.解:(1)当![]() 时,由
时,由![]() 有
有![]() 故
故![]() ,当
,当![]() 时,
时,
由![]() 求得
求得![]() ,故
,故![]()
综上讨论可知:![]() ………………………………………………(6分)
………………………………………………(6分)
(2)![]()
在![]() 时,
时,![]()
同理可求![]() 时,
时,![]()
故![]() 时,恒有
时,恒有![]() ……………………………………(12分)
……………………………………(12分)
|
![]()
(1+![]()
![]() ………………………………(6分)
………………………………(6分)
(2)由![]() 两边取模可知
两边取模可知
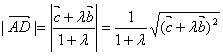 ,又
,又![]() 与
与![]() 夹角为60°
夹角为60°
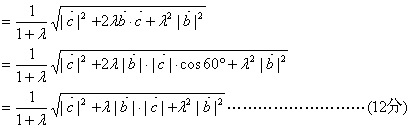
|
为G,连EH、HG、GF,则AB⊥HG又△AEB为等边三
角形则AB⊥EH
∴AB⊥面EHG,同理CD⊥面HGF
又AB//CD 则AB⊥面HGF
过H点的两个平面EHG和HGF同时垂直于直AB
∴面EHG和面HGF共同,即E、F、G、H四点共面
又EF//面ABCD ∴EF//HG,又HG//BC 故EF//BC…………(文科6分,理科4分)
|
EF=2a,HG=a,EH=GF=![]()
∴EFGH为等腰梯形,过H作HM⊥EF于是M点
![]()
又由(1)可知AB⊥面EFGH,则EF到 ABCD之距为![]()
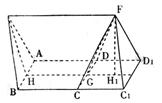
延长BC到C1,延长AD到D1,使CC1=a,DD1=a
则EF—ABC1D1为三棱柱,F—CC1D1D为四棱锥
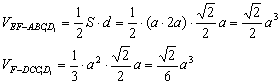
于是EF—ABCD的体积为![]() …………………………………(文科12分,理科8分)
…………………………………(文科12分,理科8分)
(3)过F作FH1垂直于HG于HG延长线上一点H1,则FH1=![]()
在底面ABC1D1中H1B=![]()
在△FBH1中,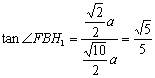 ………………………………(理科12分)
………………………………(理科12分)
20.解:(1)P(3)=![]() …………………………………………(6分)
…………………………………………(6分)
(2)(文科)![]() …………………………………………(12分)
…………………………………………(12分)
(3)(理科)![]() …………………………………………(12分)
…………………………………………(12分)
21.(文科)(1)![]() 成等差数列
成等差数列
![]()
即![]() ①
①
由![]() 求得
求得![]() ………………………………(6分)
………………………………(6分)
(2)由①式可知![]() ②
②
由①②相减得![]()
则![]() 又
又![]()
由等比数列定义可知在n≥2时,{![]() }数列为等比数列……………………(12分)
}数列为等比数列……………………(12分)
(理科)证:(1)由条件可知:![]() 再变形,得
再变形,得![]()
由![]() 叠加可知
叠加可知
![]() 而
而![]() ,则
,则![]() …………………………(6分)
…………………………(6分)
(2)![]() 可知
可知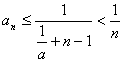
从而![]()
![]()
![]() 得证. …………………………………………………………(12分)
得证. …………………………………………………………(12分)
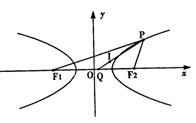
22.解:(1)∵I为△PF1F2内心,则I为PQ的内分点,又I分PQ的比为![]()
![]() 又
又![]()
![]() 可得
可得![]() ①
①
又![]() 可得
可得![]() ②
②
由①②式相除![]()
![]() 则
则![]() ……………………………………(8分)
……………………………………(8分)
(2)由![]() >1及
>1及![]()
![]() 即
即![]()
∴所求λ范围为:![]() ……………………………………(14分)
……………………………………(14分)