湖北省黄冈中学2005—2006学年度上学期高三年级检测题
数学(理科)试卷
YCY
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题(每小题5分,共60分. 每小题所给四个选项中,只有一个是符合题目要求的)
1.已知集合![]() ,则集合M的真子集个数是 ( )
,则集合M的真子集个数是 ( )
A.8 B.7 C.6 D.4
2.同时满足下列三个条件的函数是 ( )
①有反函数 ②是奇函数 ③其定义域与值域相等
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若![]() = ( )
= ( )
A.3 B.-3 C.-2 D.![]()
4.已知抛物线![]() 、
、![]() ),则“此抛物线顶点在直线顶点在直线
),则“此抛物线顶点在直线顶点在直线
![]() 下方”是“关于x的不等式ax2+bx+c<x有实数解”的 ( )
下方”是“关于x的不等式ax2+bx+c<x有实数解”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
|
与下列所给3件事吻合最好的图象顺序为 ( )
①我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学
②我骑着车以常速行驶,在途中遇到一次交通堵塞,耽搁了一些时间
③我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速
A.(1)(2)(3) B.(2)(3)(4) C.(3)(4)(1) D.(4)(1)(2)
6.已知![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]() ,则
,则![]() 的取值范
的取值范
围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() 是第二象限角,且
是第二象限角,且![]() ,下列命题正确的是 ( )
,下列命题正确的是 ( )
A.![]() B.
B.![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
8.已知![]() 是偶函数,则函数
是偶函数,则函数![]() 的图像的对称轴是 ( )
的图像的对称轴是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.要得到函数![]() 的图像,只需把函数
的图像,只需把函数![]() 的图像
的图像
( )
A.向左平移![]() 个单位 B.向右平移
个单位 B.向右平移![]() 个单位
个单位
C.向左平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
10.有一个等差数列![]() 与一个等比数列
与一个等比数列![]() ,它们的首项是一个相等的正数且第
,它们的首项是一个相等的正数且第![]() 项也相等,则第
项也相等,则第![]() 项的大小关系为 ( )
项的大小关系为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A.![]() B.
B.![]() C.
C.![]() D.
D.
12.已知数列![]() 满足
满足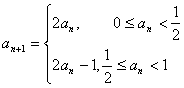 ,若
,若![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
|
|
13.设U为全集,集合![]() ,若
,若![]() )≠ ,则
)≠ ,则
a的取值范围是 .
14.设![]() ,那么
,那么![]() .
.
15.已知数列![]() 满足
满足![]() ,则数列
,则数列![]() 的通项公式
的通项公式![]() =
=
.
16.函数![]() ,它的最小正周期为
,它的最小正周期为![]() ,且其图像关于直线
,且其图像关于直线
![]() 对称,则在下面四个结论中:①图像关于点(
对称,则在下面四个结论中:①图像关于点(![]() 对称;②图像关于点
对称;②图像关于点![]() 对
对
称;③在[0,![]() 上是增函数;④在[
上是增函数;④在[![]() 上是增函数.
上是增函数.
所有正确结论的序号为 .
三、解答题(共74分. 解答须写出必要的文字说明、证明过程及演算步骤)
17.(本小题满分12分)
已知等比数列![]() 中,
中,![]() ,公比
,公比![]() ,
,![]() 又分别是某等差数列的第7项,第3项,第1项.
又分别是某等差数列的第7项,第3项,第1项.
(1)求![]() ;
;
(2)设![]() ,求数列
,求数列![]() 的前n项和Tn.
的前n项和Tn.
18.(本小题满分12分)
在△ABC中,角A、B、C所对的边分别是a、b、c,![]()
(1)求![]() 的值;
的值;
(2)若△ABC最长的边为1,求最短边的长.
19.(本小题满分12分)
已知定义域为[0,1]的函数![]() 同时满足:
同时满足:
①对于任意的![]() [0,1],总有
[0,1],总有![]() ;②
;②![]() ;③若
;③若![]() ,
,
则有![]()
(1)求f(0)的值;
(2)求![]() 的最大值.
的最大值.
20.(本小题满分12分)
已知奇函数![]() 在
在![]() 上有意义,且在(
上有意义,且在(![]() )上是增函数,
)上是增函数,![]() ,
,
又有函数![]() ,若集合
,若集合![]() ,集合
,集合![]()
(1)求![]() 的解集.
的解集.
(2)求![]()
21.(本小题满分12分)
某公司生产的摩托车,1997年每辆车的成本为4000元,出厂价(出厂价=成本+利润)为4400元,从1998年开始,公司开展技术革新,降低成本,增加效益,预计2001年每辆车的利润达到当年成本的21%,并且每辆车的出厂价不超过1997年出厂价的70.4%.
(1)2001年平均每辆摩托车的成本x至多是多少?
(2)如果以1997年的成本为基数,1997~2001年,每年成本的降低率相同(设为y),
试写出y与x的关系式.
(3)在(2)的条件下,求每年成本至少降低百分之几?(![]() 供参考)
供参考)
22.(本小题满分14分)
已知函![]() ,数列
,数列![]() 满足
满足![]() ,且
,且![]()
(1)设![]() 证明:
证明:![]()
(2)设(1)中的数列![]() 的前n项和为
的前n项和为![]() ,证明
,证明![]()
高三数学(理科)试卷参考答案
一、选择题:
1.B 2.B 3.A 4.A 5.D 6.C 7.C 8.D 9.A 10.C 11.A 12.A
二、填空题:
13.[-1,+∞![]() 14.5 15.
14.5 15.![]() 16.②④
16.②④
三、解答题:
17.(1)依题意有![]() 即
即![]() 即
即
![]() 即
即![]()
![]()
故![]()
(2)![]()
![]()
![]() 时,
时,![]()
故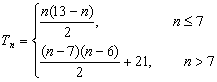 .
.
18.(1)由![]() 知B为锐角.
知B为锐角.![]()
故![]()
(2)由(1)知![]() ,故c边最长,即c=1,又
,故c边最长,即c=1,又![]() ,故b边最短
,故b边最短
![]() 由正弦定理
由正弦定理![]() 得
得
![]() 即最短边的长为
即最短边的长为![]() .
.
19.(1)对于条件③,令![]()
又由条件①知![]() 故
故![]()
(2)设![]() ,则
,则![]()
![]()
即![]() 故
故![]() 在[0,1]上是单调递增的
在[0,1]上是单调递增的
从而![]() 的最大值是
的最大值是![]()
20.(1)![]()
![]() 为奇函数且
为奇函数且![]()
![]()
又![]() 在(1,+
在(1,+![]() )上是增函数
)上是增函数 ![]()
![]() 在(-
在(-![]() ,0)上也是增函数
,0)上也是增函数
故![]() 的解集为
的解集为![]()
(2)由(1)知![]()
![]()
由![]() <-1得
<-1得![]()
即![]()
![]()
![]() ,等号成立时
,等号成立时![]()
故4-![]() ]的最大值是
]的最大值是![]()
从而![]() ,即
,即![]()
21.(1)依题意![]()
解得![]()
即2001年平均每辆摩托车的成本至多是2650元.
(2)![]()
(3)![]()
![]()
![]() 的最小值为
的最小值为![]()
即每年成本至少降低10.56%.
22.(1)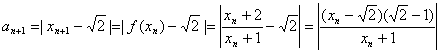
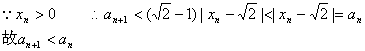
(2)由(1)的证明过程可知