绵阳市高中2006级第一次诊断性考试
数 学（理工类）
本试卷分为试题卷和答题卷两部分，其中试题卷由第I卷（选择题）和第II卷（非选择题）组成，共4页；答题卷共4页。满分150分，考试结束后将答题卡和答题卷一并交回。
第I卷（选择题，共60分）
注意事项：
1、答第1卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦擦干净后，再选涂其他答案，不能答在试题卷上。
3、参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）；
如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）；
如果事件A在一次试验中发生的概率为P，那么n次独立重复试验中恰好发生k次的概率：
。
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的，把它选出来填涂在答题卡上。
1. 复数
A. 0
B. 1 C.
i
D. 
2. “m>1,n>1”是“logmn>0”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 与函数
有相同图象的一个函数是
A. 
B.
C. 
D.
4. 某公司有N个员工，下设若干部门，现采用分层抽样方法从全体员工中抽取一个容量为n的样本（N是n的正整数倍）。已知某部门被抽取了m个员工，则这一部门的员工数为
A. 
B.
C.
D.
5. 命题“若a，b都是奇数，则a+b是偶数”的逆否命题是
A. 若a+b不是偶数，则a，b都不是奇数
B . 若a+b不是偶数，则a，b不都是奇数
C. 若a+b是偶数，则a，b都是奇数
D. 若a+b是偶数，则a，b不都是奇数
6.
设函数
在点x = 0处连续，则a的值为
A. 0
B. 
C.
D.
1
7. 若
存在，则a的值为
A. 0
B. 1
C. －1 Ｄ.
8. 设随机变量
服从正态分布N(0，1)，记
，则下列结论不正确的是
A. 
B.
C. 
D.
9.
函数
的图象具有的特征：① 原点O（0，0）是它的对称中心；②最低点是（1，2a）；③y轴是它的一条渐进线。其中正确的是
A. ①② B. ①③ C. ②③ D. ①②③
10. 曲线y=xsinx在点
处的切线与x轴、直线x=
所围成的三角形的面积为
A. 
B.
Ｃ. 
D.
11.
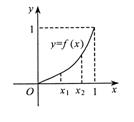
设二次函数
的图象与x轴的左右两个交点的横坐标分别为x1，x2，则
的取值范围为
A. （0，1） B. 
C.
D. 
12.
如果偶函数
在
上单调递增，则
与
大小关系是
A. 
B.
C. 
D.
无法确定
第II卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
13. 已知函数
=
。
14.
已知数列
的前n项和是
，则
=
。
15. 如果
为纯虚数，则实数a=
。
|
的任意x1，x2，下列关系：
①
；
②
③
，
其中一定正确的是 。
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。
17.
（本题满分12分）已知全集I=R，函数
的定义域为M，
，若
18.
（本题满分12分）小王参加一次知识竞赛，已知在备选的10道试题中，他能答对其中的6道。规定每次考试都从备选题中随机抽出3道题进行测试，求小王答对试题数
的概率分布及数学期望。
19.
（本题满分12分）已知f (x)是奇函数，且在定义域
内可导并满足
，解关于m的不等式
。
20.
（本题满分12分）集合A是由具备下列性质的函数f
(x)组成的：①函数f (x)的定义域是
；②函数f (x) 的值域是
；③函数f (x) 在上是增函数。试分别探究下列两小题：
（1）判断函数
及
是否属于集合A，并简要说明理由；
（2）对于（1）中你认为属于集合A的函数f (x)，不等式
是否对于任意的x≥0总成立？若不成立，为什么？若成立，请证明你的结论。
21.
（本题满分14分）已知
是定义在
上的不恒为零的函数，且对定义域内的任意x, y, f (x)都满足
。
（1）求f (1)、f (-1)的值；
（2）判断f (x)的奇偶性，并说明理由；
（3）请用数学归纳法证明
（n是正整数）
22.
（本题满分12分）讨论函数
的单调区间，并求出它的极值。