江西省五所重点协作中学2006届高三第2次月考试卷
![]() 数 学 2005-11-11
数 学 2005-11-11
重点测查内容:集合,函数,数列,三角函数 命题:韩丰
考生注意:①本试卷分试题卷和答题卷两部分,共22小题,满分150分,答题时限为120分钟;
②请把试题答案按要求填写在答题卷的相应位置,否则无论对错均不得分;
③考试结束只交答题卷。
一、选择题(本大题共12小题,单项选择,每小题5分,共60分)
1、已知集合A={椭圆},集合B={直线},则A∩B的子集数最多为
A.1个 B.2个 C.4个 D.0个
2、方程![]() 曲线形状是
曲线形状是

A. B. C. D.
3、已知数列{an}的前n项和Sn=an-1(a∈R,a≠0),则{an}
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列,或者是等比数列 D.等差、等比数列都不是
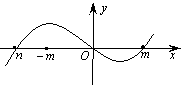
4、函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+x的解集为
 A.{x-
A.{x-![]() <x<0或
<x<0或![]() <x≤1} B.{x-1≤x<-
<x≤1} B.{x-1≤x<-![]() 或
或![]() <x≤1}
<x≤1}
C.{x-1≤x<-![]() 或
或![]() <x≤1} D.{x-
<x≤1} D.{x-![]() <x<
<x<![]() 且x≠0}
且x≠0}
5、函数f(x)=sin![]() x+cos(
x+cos(![]() x-
x-![]() )的图象相邻的两条对称轴间的距离是
)的图象相邻的两条对称轴间的距离是
 A.3π B.
A.3π B.![]() C.
C. ![]() D.
D. ![]()
6、函数![]() 的图象如图所示,则
的图象如图所示,则![]()
的值一定
A.等于0 B.小于0 C.大于0 D.小于或等于-2
7、已知函数![]() 的图象关于y轴对称,则函数
的图象关于y轴对称,则函数![]() 的图象的对称轴是直线
的图象的对称轴是直线
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、已知-1,a,b,-4,成等差数列,-1,c,d,e,-4成等比数列,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、设函数![]() (x
(x![]() R),若
R),若![]() 时,
时,![]() 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是
A.(0,1) B.(-∞,0) C.![]() ,
,![]() D.
D.![]() ,
,![]()
10、设![]() ,则
,则![]() )的值为
)的值为
A.0 B.4 C.3 D.随m变化而变化
11、关于x的方程x=ax+1,只有负根而无正根,则a的取值范围是
A.(-1,+∞) B.(1,+∞) C.[1,+∞) D.(-1,1)
12、在数列{an}中,如果存在非零常数![]() ,使得am+T =am对于任意的非零自然数
,使得am+T =am对于任意的非零自然数![]() 均成立,那么就称数列{an}为周期数列,其中
均成立,那么就称数列{an}为周期数列,其中![]() 叫数列{an}的周期。已知数列{xn}满足xn+1=xn–xn-1(n≥2),如果x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列前2005项的和是
叫数列{an}的周期。已知数列{xn}满足xn+1=xn–xn-1(n≥2),如果x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列前2005项的和是
A.668 B.669 C.1336 D.1337
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
二、填空题(本大题共4小题,每小题4分,共16分)
13、已知tan2![]() =3,则
=3,则 ![]() .
.
14、已知函数![]() 的值域是[0,+∞),则实数m的取值范围是__________________。
的值域是[0,+∞),则实数m的取值范围是__________________。
15、已知函数![]() ,则使得数列
,则使得数列![]() 成等差数列的非零常数p与q所满足的关系式为_____________.
成等差数列的非零常数p与q所满足的关系式为_____________.
16、Sn是等差数列{an}(n∈N+)的前n项和,且S6>S7>S5,给出下列结论:①d<0;②S11>0,③S12<0;④S13<0;⑤S8>S6;⑥S9>S3.则其中正确的结论的序号是 .
三、解答题:(共6小题,共74分)
▲17、已知向量![]()
(Ⅰ)求![]() 的值; (Ⅱ)若
的值; (Ⅱ)若![]() 的值.
的值.
▲18、数列{![]() }的前
}的前![]() 项和
项和![]() 满足:
满足:![]()
(Ⅰ)求数列{![]() }的通项公式
}的通项公式![]() ;
;
(Ⅱ)数列{![]() }中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
▲19、学校为推进后勤社会化改革,与桃园新区商定:由该区向建设银行贷款500万元在桃园新区为学院建一栋可容纳一千人的学生公寓,工程于2004年初动工,年底竣工并交付使用,公寓管理处采用收费还贷偿还建行贷款(年利率5%,按复利计算),公寓所收费用除去物业管理费和水电费18万元.其余部分全部在年底还建行贷款.
(Ⅰ)若公寓收费标准定为每生每年800元,问到哪一年可偿还建行全部贷款;
(Ⅱ)若公寓管理处要在2012年底把贷款全部还清,则每生每年的最低收费标准是多少元(精确到元).
(参考数据:lg1.7343=0.2391,lgl.05=0.0212,![]() =1.4774,
=1.4774,![]() =1.5513 )
=1.5513 )
▲20、已知![]() ,奇函数
,奇函数![]() 在
在![]() 上单调.
上单调.
(Ⅰ)求字母![]() 应满足的条件;
应满足的条件;
(Ⅱ)设![]() ,且满足
,且满足![]() ,求证:
,求证:![]() .
.
▲21设a∈R,f(x)为奇函数,且f(2x)=![]() ,
,
(Ⅰ)求f(x)的反函数f -1(x)及其定义域;
(Ⅱ)设g(x)=![]() ,若x∈
,若x∈![]() 时,f -1(x)≤g(x)恒成立,求实数k的取值范围。
时,f -1(x)≤g(x)恒成立,求实数k的取值范围。
▲22、已知正项数列![]() 中,
中,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上;数列
上;数列![]() 中,点
中,点![]() 在过点
在过点![]() ,斜率为2的直线上。
,斜率为2的直线上。
(Ⅰ)若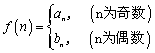 ,问是否存在
,问是否存在![]() ,使
,使![]() 成立,若存在,求出
成立,若存在,求出![]()
值;若不存在,说明理由;
(Ⅱ)对任意正整数![]() ,不等式
,不等式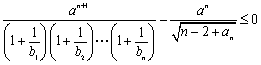 成立,求正数
成立,求正数![]() 的范围。
的范围。
江西省五所重点协作中学2006届高三第2次月考
数学参考答案及评分意见
一、 选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | C | A | B | C | D | C | D | C | C | D |
二、填空题:
13、4 14、[0,3-![]() ]∪[3+
]∪[3+![]() ,+∞);(注:区间的开闭性不对不给分)
,+∞);(注:区间的开闭性不对不给分)
15、![]() 16、①②④⑥
16、①②④⑥
▲17、(1)![]()
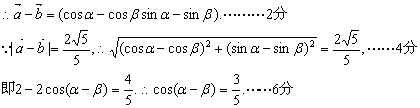
(2)![]()
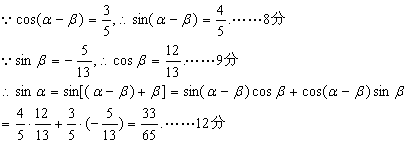
▲18、(1)当![]() 时有:
时有:![]()
两式相减得:![]() ……3′
……3′
![]()
∴数列{![]() }是首项6,公比为2的等比数列. 从而
}是首项6,公比为2的等比数列. 从而![]()
(2)假设数列{![]() }中存在三项
}中存在三项![]() ,它们可以构成等差数列,
,它们可以构成等差数列,
![]() 只能是
只能是![]() ,
,![]()
即![]() ……8′
……8′ ![]() 、
、![]() 、
、![]() 均为正整数,
均为正整数,
∴(*)式左为奇数右为偶数,不可能成立. 因此数列{![]() }中不存在可以构成等差数列的三项…12′
}中不存在可以构成等差数列的三项…12′
▲19、依题意,公寓2004年底建成,2005年开始使用.
(1)设公寓投入使用后n年可偿还全部贷款,则公寓每年收费总额为1000×80(元)=800000(元)=80万元,扣除18万元,可偿还贷款62万元.……2分
依题意有 ![]() …
…![]() .……4分
.……4分
化简得![]() . ∴
. ∴ ![]() .
.
两边取对数整理得![]() .∴ 取n=12(年).……5分
.∴ 取n=12(年).……5分
∴ 到2016年底可全部还清贷款.……6分
(2)设每生和每年的最低收费标准为x元,因到2012年底公寓共使用了8年,
依题意有![]() …
…![]() .…9分
.…9分
化简得![]() .
.
∴ ![]() (元)
(元)
故每生每年的最低收费标准为992元.……12分
▲20、(1)![]() ;…1分
;…1分 ![]() .…2分
.…2分![]() ,
,
若![]()
![]() 上是增函数,则
上是增函数,则![]() 恒成立,即
恒成立,即![]() …4分
…4分
若![]()
![]() 上是减函数,则
上是减函数,则![]() 恒成立,这样的
恒成立,这样的![]() 不存在. …5分
不存在. …5分
可得:![]() .…6分
.…6分
(2)(证法一)设![]() ,由
,由![]() 得
得![]() ,于是有
,于是有 ,
,
(1)-(2)得:![]() ,化简得
,化简得![]() ,
,
![]() ,
,![]() ,故
,故![]() ,即有
,即有![]() .
.
…12分
(证法二)假设![]() ,不妨设
,不妨设![]() ,由(1)可知
,由(1)可知![]() 在
在![]()
上单调递增,故![]() ,这与已知
,这与已知![]() 矛盾,故原假设不成立,即有
矛盾,故原假设不成立,即有![]() .…12分
.…12分
21、 (1)由f(x)是奇函数,f(-x)=-f(x)易得:a=1 3分
∴![]() ,令y=
,令y=![]() ,则2x=
,则2x=![]() >0,得-1<y<1 5分
>0,得-1<y<1 5分
从而所求反函数![]() (-1<x<1) 6分
(-1<x<1) 6分
(2)![]() ,即
,即![]() 有
有![]() 7分
7分
由对数定义知![]() ∵x∈[
∵x∈[![]() ,∴1+x>0,1-x>0,从而k>0, 8分
,∴1+x>0,1-x>0,从而k>0, 8分
∴不等式可化为k2≤1-x2在x∈[![]() 上恒成立。 9分
上恒成立。 9分
即k2≤(1-x2)min=![]() , 12分 结合k>0,得0<k≤
, 12分 结合k>0,得0<k≤![]() . 12分
. 12分
▲22、解:(Ⅰ)将点![]() 代入
代入![]() 中得
中得
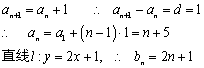 …(2分)
…(2分)
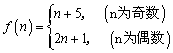 ……(4分)
……(4分)
 ……(7分)
……(7分)
(Ⅲ)由