江西省乐平市三中2006届高三数学(理科)月考试题
一、选择题：本大题共12小题，每小题5分，共60分
1．不等式
的解集为 （ ）
A．
B．
C．
D．
2.复数
等于 （ ）
A．
B．
C．
D．
3 .设
展开式中的各项系数和为
，其二项式系数和为
，则
(A) 
(B) 
(C) 0
(D) 
4.如果函数
的反函数是
，则下列等式中正确的是
（
）
（A）
（B）
（C）
（D）
5.函数
其定义域
分成了四个单调区间，则实数
满足
（
） 
（
）
（
）
（
）
6.设向量
的模等于4, 与
的夹角为,则在方向上的投影为 ( )
A.2 B.-2 C.2 D.-2
7.已知两点A（3，2）和B（－1，4）到直线
距离相等，则m值为（ ）
A．
B．
C．
D．
8.若双曲线
的渐近线l方程为
，则双曲线焦点F到渐近线l的距离为
( )
A．2 B．
C．
D．2
9.若
，则标准正态总体在区间（－3，3）内取值的概率为 A．0.9987 B．0.9974 C．0.9944 D．0.8413
10. 正四面体棱长为1，其外接球的表面积为
A.
π B.
π
C.
π D.3π
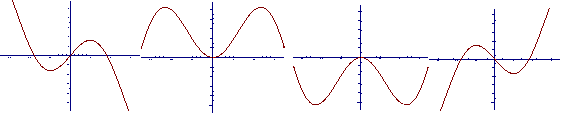11.设函数
的图象上的点
的切线的斜率为
，若
，则函数的图象大致为
A． B． C． D．
12.已知定义在R上的函数y=f (x)满足以下三个条件：①对于任意的x∈R，都有
；②对于任意的
，且
，都有f (x1)＜f (x2)；③函数y=f (x+2)的图象关于y轴对称。则下列结论中正确的是
（ ）
（A）f (4.5)＜f (7)＜f (6.5) （B）f (7)＜f (4.5)＜f (6.5)
（C）f (7)＜f (6.5)＜f (4.5) （D）f (4.5)＜f (6.5)＜f (7)
二、填空题：本大题共4小题，每小题4分，共16分.将正确答案填在题中横线上．
13.找一个非零函数
，使
，则的解析式可以是_________
14.某客运公司确定客票价格的方法是：如果行程不超过100km，票价是0.5元/km,如果超过100km,超过100km部分按0.4元/km定价,则客运票价y与行程公里数xkm之间的函数的关系式是 ____________
15．有一排标号为A、B、C、D、E、F的6个座位，请2个家庭共6人入座，要求每个家庭的任何两个人不坐在一起，则不同的入座方法的总数为______．（用数字做答）
16．下列四个命题
①分别和两条异面直线均相交的两条直线一定是异面直线.
②一个平面内任意一点到另一个平面之距离均相等，那么这两个平面平行.
③一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角的平面角相等或互补.
④过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交.
其中正确命题的编号是 .
三、解答题(共6小题)
17．（本题12分）
A、B、C为△ABC的三内角，且其对边分别为a、b、c.若
,
，且
·
＝.
（1）求角A的大小；
（2）若a＝2，三角形面积S＝，求b+c的值.
18．（本小题12分）
甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率为0.92.
（1）求该题被乙独立解出的概率；
（2）求解出该题的人数
的数学期望和方差.
19. （本小题12分）
已知函数
在区间
上是增函数.
(Ⅰ) 求实数
的取值范围；
(Ⅱ) 若数列
满足：
，
证明：
.
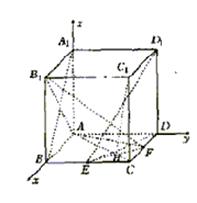
20．如图，在棱长为1的正方体ABCD—A1B1C1D1中，点E是棱BC的中点，点F是棱
CD上的动点.
（I）试确定点F的位置，使得D1E⊥平面AB1F；
（II）当D1E⊥平面AB1F时，求二面角C1—EF—A的大小（结果用反三角函数值表示）.
|
21．（本小题满分12分）
已知函数
（1）若
的表达式；
（2）若函数
上单调递增，求b的取值范围.
22．（本小题满分14分）
已知椭圆C的中心在原点，焦点在x轴上，一条经过点（3，－）且方向向量为
的直线l交椭圆C于A、B两点，交x轴于M点，又
.
（1）求直线l方程； （2）求椭圆C长轴长取值的范围.
月考试题答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | B | D | B | B | C | C | B | A | A |
二、填空题
13)
14 ) y=
15) 72 16) ②
三、解答题
17：解析:（1）∵，，且·＝，
∴－cos2＋sin2＝， 即－cosA＝，又A∈(0，p)，
∴A＝p,
（2）S△ABC＝bc·sinA＝b·c·sinp＝
，∴bc＝4,
又由余弦定理得：a2=b2+c2－2bc·cos120°＝b2+c2+bc ,
∴16＝(b+c)2，故b+c＝4.
18、解：（1）记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1，乙为P2.（2分）
则P（A）=P1=0.6,P(B)=P2
|
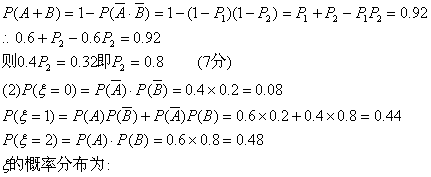
| 0 | 1 | 2 |
| P | 0.08 | 0.44 | 0.48 |
19、(Ⅰ) 解：∵在上是增函数，
∴
，即
对
恒成立.
∵
，
∴
为所求.
(Ⅱ) 证：先用数学归纳法证明
.
① 当
时，
，不等式成立.
② 假设当
时不等式成立，即
，则
时，
由(Ⅰ)知，当
时，
在上是增函数，
∵，
，
∴
，即
，则时不等式也成立.
由① ②知，对一切
都成立.
由
知：
，即
.
综上所述，.
20、解法一：（I）连结A1B，则A1B是D1E在面ABB1A；内的射影
∵AB1⊥A1B，∴D1E⊥AB1，
于是D1E⊥平面AB1F
D1E⊥AF.
连结DE，则DE是D1E在底面ABCD内的射影.
∴D1E⊥AFDE⊥AF.
∵ABCD是正方形，E是BC的中点.
∴当且仅当F是CD的中点时，DE⊥AF，
即当点F是CD的中点时，D1E⊥平面AB1F.…………6分
（II）当D1E⊥平面AB1F时，由（I）知点F是CD的中点.
又已知点E是BC的中点，连结EF，则EF∥BD. 连结AC，
设AC与EF交于点H，则CH⊥EF，连结C1H，则CH是
C1H在底面ABCD内的射影.
C1H⊥EF，即∠C1HC是二面角C1—EF—C的平面角.
在Rt△C1CH中，∵C1C=1，CH=
AC=
，
∴tan∠C1HC=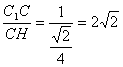
.
∴∠C1HC=arctan
，从而∠AHC1=
.
故二面角C1—EF—A的大小为.
解法二：以A为坐标原点，建立如图所示的空间直角坐标系
（1）设DF=x，则A（0，0，0），B（1，0，0），D（0，1，0），
A1（0，0，1），B（1，0，1），D1（0，1，1），E
，F（x，1，0）
（1）当D1E⊥平面AB1F时，F是CD的中点，又E是BC的中点，连结EF，则EF∥BD. 连结AC，设AC与EF交于点H，则AH⊥EF. 连结C1H，则CH是C1H在底面ABCD内的射影.
∴C1H⊥EF，即∠AHC1是二面角C1—EF—A的平面角.
|
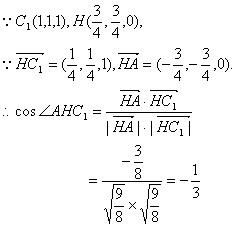
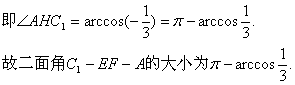
21．（本小题满分12分）
解：（1）
（2）
| x |
| －2 |
|
|
|
|
| + | 0 | － | 0 | + |
|
|
| 极大 |
| 极小 |
|
上最大值为13……………………………………………………（12分）
（3）上单调递增
又
依题意
上恒成立.
①在
|
③在
综合上述讨论可知，所求参数b取值范围是：b≥0………………………………（12分）
22、解：（1）直线l过点（3，－）且方向向量为
化简为：
…………（4分）
（2）设直线
交于两点A（x1,y1），B（x2,y2），和x轴交于M（1，0）
由
………………………………………………（7分）
将
…………………………………………①
|
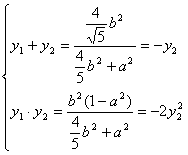
由②2/③ 知：32b2=（4b2+5a2）（a2－1）…………………………………………（10分）
化为
………………………………………………④
对方程①求判别式，且由△>0
即
化简为：
………………………………………………⑤
由④式代入⑤可知：
又椭圆的焦点在x轴上，
则
由④知：
因此所求椭圆长轴长2a范围为（