北京朝阳02-03年上学期高一数学期末统一考试
（考试时间100分钟 满分100分）
一、 选择题：本大题共10个小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的，把所选项前的字母填在题后括号内
（1） 函数y=log2(2－x)的定义域是
（A）（2，+∞） （B）（0，2） （C）（－∞，2） （D）（－2，2）
（2） 下列各组函数中，图象相同的是
（A）y=x和y=
（B）y=1和y=(x-1)0
（C）y=│x-1│和y=
（D）y=
和y=x
（3） 在等差数列｛an｝中，已知a4+a6=8,a2=3,则a8=
(A)9 （B）15 （C）17 （D）21
（4） 已知P：│x-2│≤3，q：x≥－1或x≤5，则p是q的
（A）充分不必要条件
（5）
不等式
＞0的解集是
（A）｛x│x＜－1，或1＜x＜2 (B)｛x│－1＜x＜1，或x＞1＝
（C）｛x│－1＜x＜1，或x＞2 (D)｛x│x＞2｝
（6） 函数y=ax+b与y=logbx在同一坐标系内的图象是
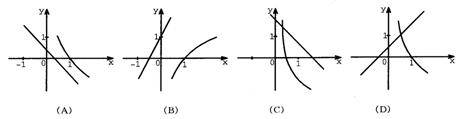
（7） 已知数列｛an｝的通项公式an=22n-1，Sn表示｛an｝的前n项和，则S4等于
（A）682 （B）170 （C）85 （D）42
（8） 已知f(x)是R上的奇函数，当x∈（0，+∞）时f（x）=x（1+x），则当x∈（－∞，0）时，f（x）的解析式为
（Ａ）－x（1－x） （Ｂ）x（1－x） （Ｃ）－x（1+x） （Ｄ）x（1+x）
（9） 函数f（x）=a-│x│(a＞)的值域是
（A）（0，+∞） （Ｂ）
（Ｃ）
（Ｄ）（０，１）
（10）
已知数列｛an｝的通项公式为an=n－
（n∈N*），则数列｛an｝
（A）有最小项 （Ｂ）有最大项 （Ｃ）无最小项 （Ｄ）有两项值相同
二、 填空题：本大题共４小题，每小题４分，共１６分，把答案填在题中横线上。
(11) 已知f（x－1）=－2x+1，则f（－２）＝ .
(12)数列｛an｝的前n项和Sn=2n2+n－1，则数列｛an｝的通项公为 。
(13)已知p：1∈｛1，2｝，q：｛1｝∈｛1，2｝，则①“p且q”为假；②“p或q”为真；③“非p”为真，其中的真命题的序号为 .
（14）设函数y=2x的图象为C，C关于直线x=－1对称的图象为C′，则C′所对应的函数解析式为 .
三、解答题：（本大题共5个小题，共44分，解答题应写出文字说明，证明过程或演算步骤。）
（15）（本小题满分8分）
已知全集为R，集合A=｛x│x2－2x－3≤0｝，B=｛x│2x-1＜1
（Ⅰ）求LRA； （Ⅱ）求A∩（LRB）.
（16）（本小题满分8分）
已知数列｛an｝是等差数列，且a23=49,a32=67.
(Ⅰ)求数列｛an｝的通项公式an；
（Ⅱ）该数列在20至50之间共有多少项？求出这些项的和.
（17）（本小题满分9分）
用函数单调性定义证明，函数f(x)=x3+
在上是增函数 .
（18）（本小题满分9分）
某地区现有居民住房的总面积am2，其中需要拆除的旧住房面积占了住房总面积的50%，当地政府决定，在每年拆除一定数量旧房的情况 下，仍以10%的住房增长率建设新房。
（Ⅰ）若10年后该地区的住房总面积恰好比目前翻一翻，那么每年应拆除的旧住房总面积x是多少？（计算参考数据1.110≈2.6）
（Ⅱ）在（Ⅰ）的条件下过10年还未拆除的旧住房总面积占当时住房总面积的百分比是多少（保留小数点后面1位）
（重点校做，普通校选做）
（19）（本小题满分10分）
设函数f（x）=loga（x+b）（a＞0且a≠1），f（x）的反函数f－1（x）的图象与直线y=x的两个交点的横坐标分别为0、1.
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）当点（x,y）是y=f（x）图象上的点时，点
是函数y=g(x)上的点，求函数y=g(x)的解析式：
（Ⅲ）在（Ⅱ）的条件下，当g
－f(x)≥0时，求x的取值范围（其中k是常数，且k≥
）.
（19）（本小题满分10分）
设函数f（x）=loga（x+b）（a＞0且a≠1），f（x）的反函数f－1（x）的图象与直线y=x的两个交点的横坐标分别为0、1.
（Ⅱ）当点（x,y）是y=f（x）图象上的点时，点是函数y=g(x)上的点，求函数y=g(x)的解析式：
（Ⅲ）在（Ⅱ）的条件下，当g－f(x)≥0时，求x的取值范围（其中k是常数，且k≥）.