高三数学模拟(一)

江苏南京02-03年高三数学模拟(一)

说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分.考试时间120分钟.

参考公式：

如果事件A、B互斥，那么

P（A+B）=P（A）+P（B）

如果事件A、B相互独立，那么

P（A·B）=P（A）·P（B）

如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的概率

正棱锥、圆锥的侧面积公式

S_锥侧=cl

其中c表示底面周长，l表示斜高或母线长

球的体积公式

V_球=πR³

其中R表示球的半径

第Ⅰ卷(选择题　共60分)

一、选择题(本大题共12小题,每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)

1.设M和m分别表示函数y=2sinx－1的最大值和最小值，则M+m等于

A.1　　　　　　　　　　 B.2　　　　　　　　C.－2　　 　　　　　 D.－1

2.设集合M={xx²－x＜0,x∈R,N={xx＜2,x∈R,则

A.NM　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.M∩N=M　　　　　　　　　　　　　　　　

C.M∪N=M　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.M∪N=R

3.若＜＜0，则下列结论不正确的是

A.a²＜b² B.ab＜b²

C. +＞2　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.a+b＞a+b

4.直线l₁，l₂互相平行的一个充分条件是

A.l₁，l₂都平行于同一个平面

B.l₁，l₂与同一个平面所成的角相等

C.l₁平行于l₂所在的平面

D.l₁，l₂都垂直于同一个平面

5.若二项式（－）ⁿ的展开式的第5项是常数项，则自然数n的值为

A.6　　　　　　　　　　　　　　　　　　 B.10　　　　　　　　　　　　　　 C.12　　　　　　　　　　　　　　　　　 D.15

6.已知f(x)=sinx+cosx,则f()的值为

A. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

7.函数y=log₂(1－x)的图象是

8.椭圆x²+my²=1的焦点在y轴上，长轴长是短轴长的两倍，则m的值为

A. 　　　　　　　　　　　　　　　　 B. 　　　　　　　　　　　　　C.2　　　　　　　　　　　　　　　D.4

9.若曲线f(x)=x⁴－x在点P处的切线平行于直线3x－y=0，则点P的坐标为

A.（1，3）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.（－1，3）

C.（1，0）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.（－1，0）

10.已知函数y=f(x)是R上的偶函数，且在（－∞，0]上是减函数，若f(a)≥f(2)，则实数a的取值范围是

A.a≤2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.a≤－2或a≥2

C.a≥－2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.－2≤a≤2

11.如图，E、F分别是三棱锥P－ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为

A.60°　　　　　　　　　　　　　　　　　　  B.45°

C.30°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.120°

12.圆心在抛物线y²=2x(y＞0)上，并且与抛物线的准线及x轴都相切的圆的方程是

A.x²+y²－x－2y－=0　　　　　　　　　　　　　　　　　　　　　　　　　

B.x²+y²+x－2y+1=0

C.x²+y²－x－2y+1=0　　　　　　　　　　　　　　　　　　　　　　　　　　　

D.x²+y²－x－2y+=0

第Ⅱ卷(非选择题　共90分)，

二、填空题(本大题共4小题,每小题4分，共16分.把答案填在题中横线上)

13.若S_n是数列{a_n}的前n项的和，S_n=n²,则a₅+a₆+a₇=_____.

14.若x、y满足　2x+y≤8,

则z=x+2y的最大值为_____.

　　　　　　　 x+3y≤9,

x≥0,

y≥0,

15.有A、B、C、D、E五名学生参加网页设计竞赛，决出了第一到第五的名次，A、B两位同学去问成绩，老师对A说：“你没能得第一名”.又对B说：“你得了第三名”.从这个问题分析，这五人的名次排列共有_____种可能（用数字作答）.

16.若对n个向量a₁,a₂,…,a_n存在n个不全为零的实数k₁,k₂,…,k_n,使得k₁a₁+k₂a₂+…+k_na_n=0成立，则称向量a₁,a₂,…,a_n为“线性相关”.依此规定，能说明a₁=（1，0），a₂=（1，－1），a₃=（2，2）“线性相关”的实数k₁,k₂,k₃依次可以取_____（写出一组数值即可，不必考虑所有情况）.

三、解答题(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）

17.(本小题满分12分)

已知cos(+x)=，求的值.

18.(本小题满分12分)

已知等比数列｛a_ｎ｝的公比为q，前n项的和为S_n，且S₃，S₉，S₆成等差数列.

(1)求q³的值；

(2)求证a₂,a₈,a₅成等差数列.

19.(本小题满分12分)

一个口袋中装有大小相同的2个白球和3个黑球.

(1)从中摸出两个球，求两球恰好颜色不同的概率；

(2)从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率.

注意：考生在（20甲）、（20乙）两题中选一题作答.如果两题都答，只以（20甲）计分.

20.(本小题满分12分)

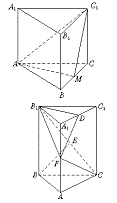（甲）如图，正三棱柱ABC－A₁B₁C₁的底面边长为A,点M在边BC上，△AMC₁是以点M为直角顶点的等腰直角三角形.

（1）求证点M为边BC的中点；

（2）求点C到平面AMC₁的距离；

（3）求二面角M－AC₁－C的大小.

（乙）如图，直三棱柱ABC－A₁B₁C₁中,底面是以∠ABC为直角的等腰直角三角形，AC=2a,BB₁=3a,D为A₁C₁的中点,E为B₁C的中点.

（1）求直线BE与A₁C所成的角；

（2）在线段AA₁上是否存在点F，使CF⊥平面B₁DF，若存在，求出；若不存在，说明理由.

21.(本小题满分12分)

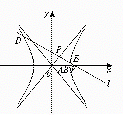
已知双曲线C：－=1(a＞0,b＞0),B是右顶点，F是右焦点，点A在x轴正半轴上，且满足、、成等比数列，过F作双曲线C在第一、三象限的渐近线的垂线l，垂足为P.

（1）求证：·=·；

（2）若l与双曲线C的左、右两支分别相交于点D、E，求双曲线C的离心率e的取值范围.

22.(本小题满分14分)

设函数f（x）＝x²+2bx+c(c＜b＜1),f(1)=0.且方程f(x)+1=0有实根.

(1)证明：－3＜c≤－1且b≥0；

(2)若m是方程f(x)+1=0的一个实根，判断f(m－4)的正负并加以证明.