宜昌市2006届高三第一次调研试题
理科数学
一.选择题(每小题所给四个选项中,只有一个符合题目要求,每小题5分,共60分)
1.设集合M=![]() x+y>2,且xy>0
x+y>2,且xy>0![]() ,N=
,N=![]() x>1,且y>1
x>1,且y>1![]() ,则有( )
,则有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
3.已知三个力![]() ,
,![]() ,
,![]() 同时作用于某物体上一点,为使物体保持平衡,现加上一个力
同时作用于某物体上一点,为使物体保持平衡,现加上一个力![]() ,则
,则![]() 等于( )
等于( )
A.(-1,-2) B.(1,-2) C.(-1,2) D.(1,2)
4.等差数列![]() 中,S9=-36,S13=-104,等比数列
中,S9=-36,S13=-104,等比数列![]() 中,
中, ![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.-
B.-![]() C.±
C.± ![]() D.无法确定
D.无法确定
5.![]() 是
是![]() 的( )
的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分不必要条件
6.函数![]() 的图象无论经过平移还是关于某条直线对称翻折后仍不能与
的图象无论经过平移还是关于某条直线对称翻折后仍不能与![]() 的图象重合,则
的图象重合,则![]() 是( )
是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.以椭圆![]() 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线![]() 的渐近线相切的圆的方程是( )
的渐近线相切的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”。在下面五个点M(1,1),N(1,2),P(2,1),Q(2,2),G(2,![]() )中,“好点”的个数为( )
)中,“好点”的个数为( )
A.0个 B.1个 C.2个 D.3个
9.已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,则该数列前26项和为( )
,则该数列前26项和为( )
A.0 B. -1 C.-8 D.-10
10.使![]() 为奇函数,且在
为奇函数,且在![]() 上是减函数的
上是减函数的![]() 的一个
的一个
值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知函数![]() , 定义在R上的奇函数
, 定义在R上的奇函数![]() ,当
,当![]() 时
时![]() ,则函数
,则函数![]() 的大致图象为( )
的大致图象为( )
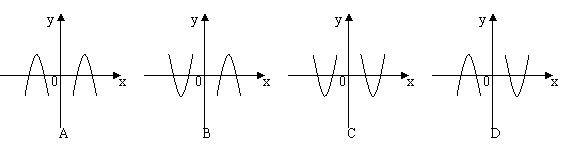
![]()
12.已知曲线![]() 与其关于点(1,1)对称的曲线有两个不同的交点A、B,如果过这两个交点的直线的倾斜角是
与其关于点(1,1)对称的曲线有两个不同的交点A、B,如果过这两个交点的直线的倾斜角是![]() ,则实数a的值是( )
,则实数a的值是( )
A.1
B.![]() C.2
D.3
C.2
D.3
二.填空题(本大题共4小题,每小题4分,共16分)
13.函数![]() 的单调减区间是 。
的单调减区间是 。
14.将直线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 所得直线方程是
。
所得直线方程是
。
15.已知关于x的不等式![]() 的解集为M,若
的解集为M,若![]() 且
且![]() ,则实数a取值范围是
。
,则实数a取值范围是
。
16.若函数![]() 的定义域为R,若存在常数
的定义域为R,若存在常数![]() ,使
,使![]() 对一切实数均成立,则称
对一切实数均成立,则称![]() 为
为![]() 函数,给出下列函数:
函数,给出下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
⑤![]() 是定义域在R上的奇函数,且满足对一切实数均有
是定义域在R上的奇函数,且满足对一切实数均有![]() 。
。
其中是![]() 函数的序号为
。
函数的序号为
。
三.解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分12分)在![]() 中 ,
中 ,![]() ,
,![]() ,
,![]()
(1)求![]() 值;(2)求边
值;(2)求边![]() 的长。
的长。
18.(本题满分12分)已知各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,
,![]() ,P>0且P≠1,数列
,P>0且P≠1,数列![]() 满足
满足![]() 。
。
(1)求![]() ,
,![]() ;
;
(2)若P=![]() ,设数列
,设数列![]() 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
19.(本题满分12分)某人上午7时乘摩托艇以匀速v km/h(4≤v≤20)从A港出发前往50 km处的B港,然后乘汽车以匀速w km/h(30≤w≤100)自B港向300 km处的C市驶去,在同一天的16时至21时到达C市,设摩托艇、汽车所需的时间分别是![]() h、
h、![]() h,若所需经费
h,若所需经费![]() 元,那么v、w分别为多少时,所需经费最少?并求出这时所花的经费。
元,那么v、w分别为多少时,所需经费最少?并求出这时所花的经费。
20.(本题满分12分)已知向量![]() 满足
满足![]() ,且
,且![]() ,其中
,其中![]() 。
。
(1)试用k表示![]() ,并求出
,并求出![]() 的最大值及此时
的最大值及此时![]() 的夹角
的夹角![]() 的值。
的值。
(2)当![]() 取得最大值时,求实数
取得最大值时,求实数![]() ,使
,使![]() 的值最小,并对这一结果作出几何解释。
的值最小,并对这一结果作出几何解释。
21.(本题满分12分)已知集合A={xx―a<ax,a>0},若函数![]() (
(![]() )是单调函数,求a的取值范围。
)是单调函数,求a的取值范围。
22.(本题满分14分)F1、F2为双曲线![]() 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:![]() ,
,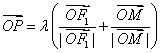 (λ>0)
(λ>0)
(1)求此双曲线的离心率;
(2)若过点N(![]() ,
,![]() )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且![]() ,
,![]() ,求双曲线C和直线AB的方程。
,求双曲线C和直线AB的方程。
宜昌市2006届高三第一次调研试题理科数学参考答案
一.BBDCAD ACDABC
二.![]() ;
;![]() ;
;![]() ;①④⑤
;①④⑤
三.17解:(1)![]()
又![]() ,故在
,故在![]() 中,
中,![]() 、
、![]() 是锐角 ∴
是锐角 ∴![]() ,
,![]()
∴![]() (6分)
(6分)
(2) ![]()
由正弦定理 ![]() 解得
解得![]() ;b=6
;b=6
∴![]() ∴
∴![]() (12分)
(12分)
18解:当n=1时,![]() ,∴
,∴![]()
当n≥2时,![]() ,∴
,∴![]() ,
,
(1)∴![]() ;
;![]() (6分)
(6分)
(2)![]() ,错位相减得
,错位相减得![]() (12分)
(12分)
19解:依题意: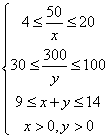 ,考察
,考察![]() 的最大值
(6分)
的最大值
(6分)
作出可行域,平移![]() ,当等值线经过点(4,10)时Z取得最大值38。 (10分)
,当等值线经过点(4,10)时Z取得最大值38。 (10分)
故当v=12.5、w=30时所需经费最少,此时所花的经费为93元。 (12分)
20解:(1)![]()
![]()
![]() ,此时
,此时![]()
即![]() 的最大值为
的最大值为![]() ,此时
,此时![]() 的夹角
的夹角![]() 的值为
的值为![]() 。
(6分)
。
(6分)
(2)由题意![]() ,故
,故![]()
∴![]() 当
当![]() 时,
时,![]() 的值最小,此时
的值最小,此时![]()
即当![]() 时,
时,![]() 的值最小。
(12分)
的值最小。
(12分)
21解:x―a<axÛ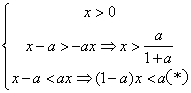
对于(*)当![]() 时
时![]() ;当
;当![]() 时
时![]()
∴当![]() 时原不等式解集为
时原不等式解集为![]() ;当
;当![]() 时解集为
时解集为![]() 。 (6分)
。 (6分)
![]() ,当
,当![]() 时显然不单调。
时显然不单调。
![]() 的单调区间为
的单调区间为![]() 和
和![]()
![]()
而![]() ,故
,故![]()
![]() 即:
即:
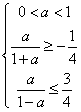 ∴
∴![]() (12分)
(12分)
22解:(1)依题意四边形OF1PM为菱形,设P(x,y)则F1(-c,0),M(![]() ,y)
,y)
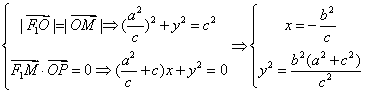 代入
代入![]() 得
得
![]() 化简得e=2
(4分)
化简得e=2
(4分)
(2)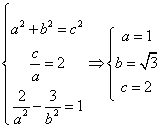 ∴双曲线C的方程为
∴双曲线C的方程为![]() (8分)
(8分)
(3)题意为过B2的直线交曲线C于A、B两点,且![]()
设直线AB:![]() 代入
代入![]() 得
得![]()
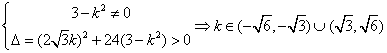
设B1(x1,y1),B2(x2,y2)由![]()
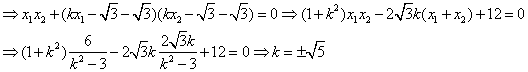
∴直线AB的方程为![]() (14分)
(14分)