数学理科 模拟试卷四
一、选择题
1. 函数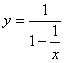 
的定义域是：( )
（Ａ） {x｜x∈R且x≠0}
（Ｂ） {x｜x∈R且x≠1}
（Ｃ） {x｜x∈R或x≠0或x≠1}
（D） {x｜x∈R且x≠0且x≠1}
2. 已知集合M={3,a},
N={x｜x
-3x＜0,x∈Z},M∩N={1},又P=M∪N.
那么集合P的子集共有：( )
（Ａ） 3个 （Ｂ） 7个
（Ｃ） 8个 （Ｄ） 16个
3. 如果a、b异面直线，那么只须满足条件( )
（Ａ） a⊥b是平面α, b是α的一条斜线
（Ｂ） a∥直线c, b与c相交于点A且a与b不相交
（Ｃ） a平面α，且b平面α，且a与b不平行
（Ｄ） a平面α，b平面β，α∩β=l且a与b不相交
4. 点P(1,3)关于直线x+y=0的对称点坐标是：( )
（Ａ） (-3，-1) （Ｂ） (-1，-3)
（Ｃ） (3，1) （Ｄ） (-3，1)
5. 已知2sinx=1+cosx，则
的值为：( )
（Ａ） 
（Ｂ） 或不存在
（Ｃ） 2 （Ｄ） 2或
6. 一个火车站有5股岔道，每股岔道只能停放一列火车，现要停放3列不同的火车,
不同的停放方法共有：( )
（Ａ）C
种
（Ｂ） P种
（Ｃ） P·P
种
（Ｄ） CC种
7. 设
，下面式子成立的是：( )
（Ａ） sin(arc sin x)=x （Ｂ） arc cos (cosx)=x
（Ｃ） tg(arc tg x)=x （Ｄ） arc tg (tg x)=x
8. 函数y=log
(cosx-sinx)的单调递减区间是：( )
（Ａ） [ kπ,kπ+
) (k∈Z)
（Ｂ） [ kπ,kπ+
] (k∈Z)
（Ｃ） [ kπ,kπ-) (k∈Z)
（Ｄ） ( kπ-,kπ ] (k∈Z)
9. 动点P(x,y)在抛物线y=2x+1上移动，那么点P与点Q(0，-1)的连线的中
点M的轨迹方程是：( )
（Ａ） y=2x
（Ｂ） y=4x
（Ｃ） y=6x
（Ｄ） y=8x
10. 有一个三棱锥的一条棱长为3，其余五条棱长都是2，那么这个三棱锥的体积
等于：( )
（Ａ） 
（Ｂ）
（Ｃ） 
（Ｄ）
11. 如果数列{a
}是等比数列，且a100=i，a200=10，那么a300= ( )
（Ａ） 100 （Ｂ） -100
（Ｃ） 100i （Ｄ） -100i
12. 一个圆台的母线长是上下底面半径的等差中项，且侧面积为18πcm，
那么母线长是：( )
（Ａ） 9cm
（Ｂ） 
（Ｃ） 3cm
（Ｄ） 
cm
13. 极限 
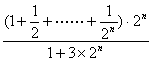的值等于：( )
（Ａ） 0 （Ｂ） 1
（Ｃ） 
（Ｄ）
14. 在复平面上，复数z满足arg(z-3)=45°，则
的最大值是：( )
（Ａ） 
（Ｂ）
（Ｃ） 
（Ｄ）
15. 设α、β为参数，则下列两曲线( )
x=-cosα+1.
x=cosβ,
c1: c2: 的交点个数是
y=-sinα+
y=sinβ
（Ａ） 0个 （Ｂ） 1个
（Ｃ） 2个 （Ｄ） 4个
二、填空题
16. 方程log
(log
x)=1 的解集是：( )
（Ａ） {x｜x=
}
（Ｂ） {x｜x=
}
（Ｃ） {x｜x=
}
（Ｄ） {x｜x=
}
17. 化简：tg10°+tg50°+tg10°tg50°=( )
（Ａ） 
（Ｂ）
（Ｃ） （Ｄ）
18. 已知小球的表面积是大球表面积的
，那么小球的体积是大球体积的：( )
（Ａ） 
（Ｂ）
（Ｃ）
（Ｄ）
19. 
的展开式中，系数最大的项是：( )
（Ａ） 
（Ｂ）
（Ｃ） 
（Ｄ）
20. 如果椭圆两焦点F1(2，1)，F2(-2,3)，离心率e=0.8，则此椭圆长轴上两顶点的坐标
是：( )
（Ａ） (
，
、(-，
) （Ｂ） (-，-)、(，)
（Ｃ） (-，)、(，)
（Ｄ） (，)、(-，-)
三、解答题
21. 在△ABC中，三个内角满足sin Acos B+sin Acos C=sin C+sin B，
试判断这三角形的形状。
[解析]
22. 铁道机车运行1小时所需的成本由两部分组成：固定部分m元，变动部分与运行速度υ(千米／小时)的平方成正比例，比例系数为k(k＞0)元，如果机车匀速从甲站开往乙站，为了使成本最省，应以怎样的速度运行:( $S*A$ )
（Ａ） 
（Ｂ）
（Ｃ）
（Ｄ） 
[解析]
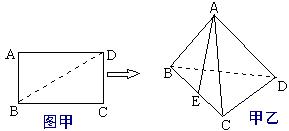
23. 矩形ABCD中，AB=3， BC=4(图甲)，沿对角线BD把△ABD折起，使点A在平
面BCD上的射影E落在BC上(图乙)，
(1) 求证：平面ACD⊥平面ABC；
(2) 求三棱锥A—BCD的体积 :( $S*C$ )
|
（Ａ）  （Ｂ）  （Ｃ） |
（Ｄ） 
[解析]
24. 已知常数a＞1，解不等式 ｜log
x｜＜｜log(ax)｜-2.
[解析]
25. 给定椭圆：
(a＞b＞0), 求与这椭圆有公共焦点的双曲线，使得以它们的
交点为顶点的四边形面积最大，( )并求相应的四边形的顶点坐标。
（Ａ）x-y=(b-a)
（Ｂ） x-y=(a-b)
（Ｃ）x-y=(b+a)
（Ｄ） x-y=(a+b)
[解析]
26. 已知函数 
的图象过原点。
(1) 若f(x-3),
f(
-1), f(x-4)成等差数列，则x的值是( )
[解析]
(2) 若φ(x)=f(x)+1, 三个正数m, n, t成等比数列，求证：φ(m)+φ(t)≥2φ(n)
[解析]
参 考 答 案
一、
1. D 2. C 3. B 4. A 5. B
6. B 7. C 8. C 9. B 10. C
11. D 12. C 13. D 14. A 15. A
二、
16. C 17. D 18. B 19. A 20. C
三、21.
[解析] ∵ sin Acos B+sin Acos C=sin C+sin B,
∴ 2sin(B+C)cos
cos
=2sincos.
∴ 4sincoscos=2sincos
∵ 0＜B＜π,0＜C＜π, ∴ -＜＜, 0＜＜π
∴ sin≠0, cos≠0 ∴ 2cos=1.
∴ cos(B+C)=0 即cos A=0 (或B+C=90°) ∴ A=90°,即△ABC为直角三角形.
22. A
[解析] 依设，1小时的成本为(m+kv) 元；
设甲、乙两站的路程为S千米，则运行所需的时间为
小时
故总成本为
.
∵s＞0, m＞0, k＞0, v＞0.
∴ y≥
.
仅当
时，即时取等号，
∴ 时，总成本y取最小值。
答：为了使机车运行时成本最小，应以速度(千米／小时)运行。
23.
(1) 略
(2) C
[解析] ∵ AE⊥平面BCD,且E在BC上,又BC⊥CD. 根据三垂线定理,得AC⊥CD
∴ CD⊥平面ABC，又CD平面ACD. ∴平面ACD⊥平面ABC. (1) ∵CD⊥平面ABC.
∴ 
=
=
·CD. 在△ADC中，AC⊥CD，AD=BC=4，
CD=AB=3.
∴ 
. 在△ABC中：
∴ 
.
∴ sin∠ABC
.
∴ 
·BC·sin∠ABC
=×3×4×
=
.又CD=3.
∴ 
··
24.
[解析]
原不等式可化为｜logx｜＜｜1+2logx｜-2.
(Ⅰ) 当logx≥0, 原不等式为logx＜2logx-1.
即 logx＞1. ∵ a＞1 ∴ x＞a.
(Ⅱ) 当-＜logx＜0时，原不等式为-logx＜2logx-1.
即 3logx＞1, logx＞. 注意到logx＜0，无解。
(Ⅲ)当logx≤-时，原不等式为 -logx＜-2logx-3.
即 logx＜-3. ∵ a＞1, ∴ 0＜x＜
.
综上讨论，并经检验，原不等式的解集为：{x｜0＜x＜或x＞a}
25. ( A )
[解析] 设双曲线的方程为
①
∵此双曲线与已知椭圆
共焦点， ∴c=a-b=α+β. ②
(c为半焦距) 设 P
(XY) 为椭圆与双曲线在第一象限内的交点，
∵ PF 既是椭圆的焦半径，又是双曲线的焦半径，
∴ 
. 解之，得 
. 代入①，得
.
以椭圆 双曲线的四个交点为顶点的四边形面积为：
≤
.
当且仅当 
时，S
=2ab.
故所求的双曲线为 x-y=
.
相应的四边形四顶点坐标是：
、
26. (1) 4
[解析] ∵ 的图象过原点，
∴ f(0)=0. 即 log
α=0. ∴ a=1.
∴ 
.
又∵ f(x-3), 
, f(x-4)成等差数列，
∴ 
∴ (x-2)(x-3)=2.解得 x=4 或 x=1. 经检验: x=1 是增根 所以 x=4
(2)
[解析] ∵ φ(x)=f(x)+1, 要证 φ(m)+φ(t)≥2φ(n),
即证 f(m)+1+f(t)+1≥2[f(n)+1]. ∵
所以只须证明 log (m+1)+log(t+1)≥2log(n+1)
即要证 (m+1)(t+1)≥(n+1) 展开得 mt+m+t+1≥n+2n+1.
即证 mt+m+t≥n+2n. 又 ∵ 三个正数m、n、t成等比数列
∴ mt=n 因此，只须证明 m+t≥2n.
由不等式平均值定理，有 m+t≥2
=2n. ∴ φ(m)+φ(t)≥2φ(n)成立。