专题诊断训练 力与曲线运动类问题（一）教师版
一、选择题
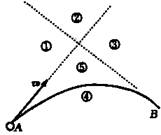1．一个物体以初速度v0从A点开始在光滑水平面上运动，一个水平力作用在物体上，物体的运动轨迹如图1中的实线所示，图中B为轨迹上的一点，虚线是过A、B两点并与轨迹相切的直线，虚线和实线将水平面划分5个区域，则关于施力物体的位置，下面说法正确的是（ AC ）
A．如果这个力是引力，则施力物体一定在④区域
B．如果这个力是引力，则施力物体一定在②区域
C．如果这个力是斥力，则施力物体可能在②区域
D．如果这个力是斥力，则施力物体一定在④区域
[考点]曲线运动的条件。
[诊断]1。物体的运动方向与合力方向不在一条直线上时，物体将做曲线运动；2。合力方向指向曲线的凹侧（内侧）
2．如图水平的木板B托着木块A一起在竖直平面内做匀速
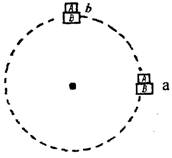圆周运动，从水平位置a沿逆时针方向运动到最高点b
的过程中（ BC ）
A．B对A的支持力越来越大
B．B对A的支持力越来越小
C．B对A的摩擦力越来越小
D．B对A的摩擦力越来越大
3．在交通事故中，测定碰撞瞬间汽车的速度对于事故责任的认定具有重要作用，《中国汽车驾驶员》杂志曾给出一个估算碰撞瞬间车辆速度的公式：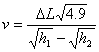
，公式中
是被水平抛出的散落在事故现场路面上的两物体A、B沿公路方向上水平距离，
分别是散落物A、B在车上时的高度。只要用米尺测量出事故车辆现场、三个量，根据上述公式就能够估算出碰撞瞬间车辆的速度，则下列叙述正确的是（
BD ）
A．A、B落地时间相同
B．A、B落地时间差与车辆速度无关
C．A、B落地时间差与车辆速度成正比
D．A、B落地时间差和车辆碰撞瞬间速度的乘积等于
4．如图所示，匀强磁场方向竖直向下.磁场中有光滑水平桌面，在桌面上平放着内壁光滑、底部有带电小球的试管.在水平拉力F作用下,试管向右匀速运动，最后带电小球能从试管口飞出,则（ BD ）
A.小球带负电
B.小球运动轨迹是一条抛物线
C.洛伦兹力对小球做正功
D.维持试管匀速运动的拉力F应逐渐增大
5．如图1所示，水平抛出的物体，抵达斜面上端P处，其速度方向恰好沿斜面方向，然后沿斜面无摩擦滑下，图2中的图象是描述物体沿x方向和y方向运动的速度－时间图象，其中正确的是 （ C ）
6．如图所示，在匀强电场中有一个原来速度几乎为零的放射性碳14原子核，它所放射的粒子与反冲核经相等时间所形成的径迹如图所示（a、b均表示长度）.那么碳14的衰变方程可能是（A）
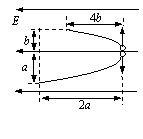A.
B. 
C. 
D. 
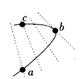
7．如图，虚线表示等势面，相邻两等势面间的电势差相等。有一带正电的小球在电场中运动，实线表示该带正电小球的运动轨迹。小球在a点的动能等于20eV，运动到b点时的动能等于2eV。若取C点为零势点，则当这个带电小球的电势能等于6eV时(不计重力和空气阻力)，它的动能等于（ C ）
A．16eV B．14eV C．8eV D．4Ev
8．如图所示画出了匀强电场的几条电场线，M、N是该电场中 的两点，一个带正电荷的离子(不计重力)仅在电场力作用下由M点运动到N点，则 ( A )
A．该离子在M点的速度不为零
B．该离子在M点的速度可能为零
C．该离子在M点的电势能小于在N点的电势能
D．该离子在M和N点的电势能哪个大不能确定
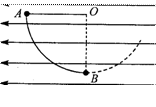9．如图所示，在水平向左的匀强电场中，一根细线一端系一个质量为m的带正电的小球，另一端固定在O点．现在让细线水平绷直，小球从A点由静止开始摆下，小球能达到并通过最低点B．则小球在最低点B处，细线的拉力可能是( BC )
A．
B．
C．
D．
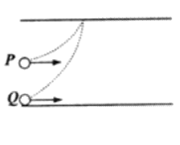10．如图所示，质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射人两平行板间的匀强电场中．P从两极板正中央射入， Q从下极板边缘处射入，它们最后打在同一点(重力不计)，则从开始射人到打到上板的过程中 ( C )
A．它们运动的时间tQ＞tp
B．它们的电势能减小量之比△Ep:△EQ=1:2
C．它们所带的电荷量之比qp : q Q=1:2
D．它们的动量增量之比 △PP:△PQ=1:2
二、说理计算题
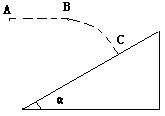11．如图所示,AB是匀强电场中的一条水平线段,长度为L,它与电场方向成θ角,某时刻一质量为m,带电量为+q的小球在电场中的A点由静止释放,小球沿直线AB运动到B点时离开电场,然后落到倾角为α的绝缘弹性斜面上的C点,C点距离AB高度为h,小球恰好能够沿原路返回A点,求：
（1）电场强度E的大小；
（2）角α的值；
（3）球从A点出发返回A点的时间；
11．解答：（1）由于出电场后球做平抛运动，在电场内运动时，其速度方向是水平的，
即合外力是水平的，由qEcosθ=mg得：
E=mg/qcosθ
（2）在电场中运动的加速度a=mgtanθ/m=gtanθ;
故出电场的速度V0=
=
出电场后只受重力作用，在到达斜面时有竖直分速度
斜面应与V0与
的合速度V垂直，所以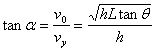
（3）球出电场的时间t1=2L/ V0=
出电场后落到斜面的时间t2=
所以往返时间T=2(t1+
t2)=2(+)
12．真空中存在空间范围足够大的、水平向右的匀强电场。在电场中，若将一个质量为m、带正电的小球由静止释放，运动中小球的速度与竖直方向夹角为37°(取sin37°=0.6, cos37°=0.8)。现将该小球从电场中某点以初速度v0竖直向上抛出。求运动过程中
（1）小球受到的电场力的大小及方向；
（2）小球从抛出点至最高点的电势能变化量；
（3）小球的最小动量的大小及方向。
12．解答：（1）根据题设条件，电场力大小
Fe=mgtan37°=
mg
电场力的方向水平向右。
（2）小球沿竖直方向做匀减速运动，速度为v，
vy = v0－gt
沿水平方向做初速度为0的匀加速运动，加速度为ax
ax=
小球上升到最高点的时间t =
，此过程小球沿电场方向位移
sx =
axt2=
电场力做功W
= Fesx=
m
小球上升到最高点的过程中，电势能减少m
（3）水平速度vx = axt，竖直速度vy = v0－gt
小球的速度v
=
由以上各式得出v=
解得当t=
时，v有最小值vmin=
v0
此时vx=
v0，vy=
，tanθ=
，即与电场方向夹角为37°斜向上
小球动量的最小值为pmin= mvmin = mv0
最小动量的方向与电场方向夹角为37°，斜向上。
13．在图14所示为一真空示波管，电子从灯丝K发出（初速度不计），经灯丝与A板间的加速电压U1加速，从A板中心孔沿中心线kO射出，然后进入两块平行金属板M、N形成的偏转电场中（偏转电场可视为匀强电场），电子进入M、N间电场时的速度与电场方向垂直，电子经过电场后打在荧光屏上的P点。已知加速电压为U1，M、N两板间的电压为U2，两板间的距离为d，板长为L1，板右端到荧光屏的距离为L2，电子的质量为m，电荷量为e。求：
（1）电子穿过A板时的速度大小；
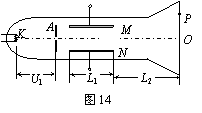（2）电子从偏转电场射出时的侧移量；
（3）P点到O点的距离。
13．解答：（1）设电子经电压U1加速后的速度为v0，根据动能定理得：
e U1=
解得：
（2）电子以速度v0进入偏转电场后，垂直于电场方向作匀速直线运动，沿电场方向作初速度为零的匀加速直线运动。设偏转电场的电场强度为E，电子在偏转电场运动的时间为t1，电子的加速度为a，离开偏转电场时相对于原运动方向的侧移量为y1，根据牛顿第二定律和运动学公式得：
F=eE,
E=
, F=ma, a =
t1=
y1=
, 解得： y1=
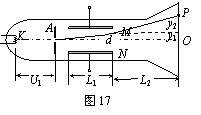（3）设电子离开偏转电场时沿电场方向的速度为vy，根据运动学公式得
vy=a1t=
电子离开偏转电场后作匀速直线运动，设电子离开偏转电场后打在荧光屏上所用的时间为t2，电子打到荧光屏上的侧移量为y2，如图17所示
t2=
， y2= vyt2 解得：y2=
P到O点的距离为 y=y1+y2=
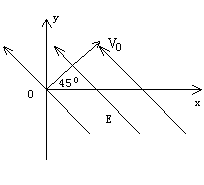14．有一个足够大的匀强电场，场强为E，方向如图所示．一电子以与
轴成
夹角的初速度
垂直于电场方向从O点射入．电子质量为
，电荷量为
，不计重力．求：
（1）电子通过轴时的位置；
（2）电子通过轴时的速度大小．
14．解答：（1）电子在电场中做类平抛运动，设电子通过轴时的位置坐标为（，0），运动时间为
，则有：
由式（1）、（2）得：
即电子通过轴的位置坐标为：（
，0）
（2）电子经过轴时，垂直于电场方向上的速度为，平行于电场方向上的速度
，则：
由（1）、（3）解得：
，电子经过轴时的速度
（或用动能定理求解）