第二轮重点突破(1)——传送带专题
连城一中 林裕光
|
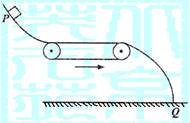
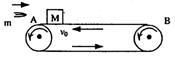
A．物块有可能落不到地面上
B．物块将仍落在Q点
C．物块将会落在Q点在左边
D．物块将会落在Q点的右边
2．如图，传送带与水平面之间夹角θ=37°，并以10 m/s的速度匀速运行，在传送带A端轻轻地放一个小物体，若已知该物体与传送带之间动摩擦因数为μ=0.5，传送带A端到B端的距离 S＝16m，则小物体从A端运动到B端所需的时间
可能是（ ）（g＝10 m/s2）
A．1.8s B．2.0s
C．2.1s D．4.0s
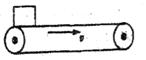
3．对如图所示的皮带传动装置，下列说法中正确的是 （ ）
|
B．B轮带动A轮沿逆时针方向旋转
C．C轮带动D轮沿顺时针方向旋转
|
4．如图所示，传送带的水平部分长为L，传动速率为v，
在其左端无初速释放一小木块，若木块与传送带间的动摩擦因
数为
，则木块从左端运动到右端的时间可能是（ ）
A．
B．
C．
D．
5．（16分）一条传送带始终水平匀速运动，将一个质量为20kg的货物无初速地放到传送带上，货物从放上到跟传送带一起匀速运动，经过的时间为0.8s，滑行的距离是0.8m，则货物与传送带间的动摩擦因数μ为多大？这个过程中，动力对传送带多做多少功？
6
|
的初速度水平地滑上水平传送带，已知旅行包与皮带之间的动摩擦因子为
本题中g取10m/s2.试讨论下列问题：
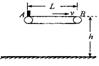
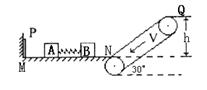
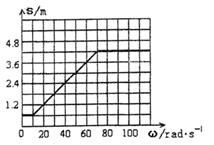
（1）若传送带静止，旅行包滑到B端时，人若没有及时取下，
旅行包点将从B端滑落，则包的落地点距B端的水平距离又是多少？
（2）设皮带轮顺时针匀速运动，且皮带轮的角速度
，旅行包落地点距B端的水平距离又是多少？
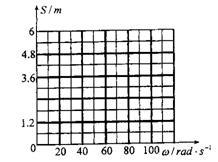
（3）设皮带轮以不同的角速度顺时针匀速转动，画出旅行包落地点距B端的水平距离S随皮带轮的角速度
变化的图像。
|
7．（18分）如图，已知传送带两轮的半径r=1m，传动中传送带不打滑，质量为1kg的物体从光滑轨道A点无初速下滑（A点比B点高h=5m），物体与传送带之间的动摩擦因数
，当传送带静止时，物体恰能在C点离开传送带，则
（1）BC两点间距离为多少？
（2）若要使物体从A点无初速释放后能以最短时间到达C点，轮子转动的角速度大小应满足什么条件？
（3）当传送带两轮以12rad/s的角速度顺时针转动时，物体仍从A点无初速释放，在整个过程中物体与皮带系统增加的内能为多少？
8、如图11所示，一平直的传送带以速度V=2m/s做匀速运动，传送带把A处的工件运送到B处，A、B相距L=10m。从A处把工件无初速地放到传送带上，经过时间t=6s,能传送到B处，欲用最短的时间把工件从A处传送到B处，求传送带的运行速度至少多大？
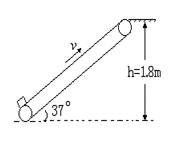9、传送带以恒定速度υ=1.2m/S运行, 传送带与水平面的夹角为37º。现将质量m=20kg的物品轻放在其底端，经过一段时间物品被送到1.8m高的平台上，如图所示。已知物品与传送带之间的摩擦因数μ=0.85，则
（1）物品从传送带底端到平台上所用的时 间是多少？
（2）每送一件物品电动机需对传送带做的 功是多少？
10.将一个粉笔头轻放在2 m/s的恒定速度运动的水平传送带上后，传送带上留下一条长度为4m的划线；若使该传送带改做匀减速运动（加速度的大小为1．5 m/s2），并且在传送带开始做匀减速运动的同时，将另一支粉笔头放在传送带上，该粉笔头在传送带上能留下一条多长的划线?(g取10 m/s2)
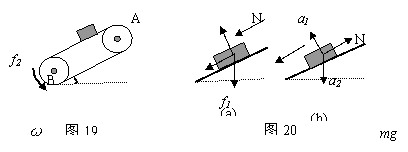
11、如图19所示，传送带与地面的倾角θ=37ｏ，从A到B的长度为16ｍ，传送带以V0=10m/s的速度逆时针转动。在传送带上端无初速的放一个质量为0.5㎏的物体，它与传送带之间的动摩擦因数μ=0.5，求物体从A运动到B所需的时间是多少？(sin37ｏ=0.6,cos37ｏ=0.8)
12．如图所示，水平传送带AB长为L，质量为M的木块随传送带一起以
的速度向左匀速运动（传送带速度恒定），木块与传送带间的动摩擦因数，且满足
。当木块运动至最左端A点时，一颗质量为m的子弹以
水平向右的速度射入木块并留在其中，求：
（1）子弹击中木块的过程中损失的机械能；
|
13．如图所示，光滑水平面MN上放两相同小物块A、B，左端挡板处有一弹射装置P，右端N处与倾斜皮带理想连接，使带保持运行速度为V=4m/s，两端高度差为h=1.6m，物块A、B与皮带间滑动摩擦因素
，皮带倾角为
。已知物块A、B质量均为mA=mB=1kg。开始时A、B静止，A、B间压缩一轻质弹簧，贮有弹性势能Epk=16J。现解除锁定，弹开A、B。求：
（1）物块B沿皮带上滑的最大高度。
（2）物块B滑回水平面MN的速度VB。
（3）若弹开后B不能上滑至平台Q，将下滑至水平面MN，与被弹射装置P弹回的A，在水平面上相碰，且A、B碰后互换速度，则弹射装置P必须给A做多少功才能让AB碰后B能滑上平台Q。
|
14．一传送带装置示意图如图2所示，其中传送带经过AB区域时是水平的，经过BC区域时变为圆弧形（圆弧由光滑模板形成，为画出），经过CD区域时是倾斜的，AB和CD都与BC相切。现将大量的质量均为m的小货箱一个一个在A处放到传送带上，放置时初速为零，经传送带运送到D处，D和A的高度差为h。稳定工作时传
送带速度不变，CD段上各箱等距排列，相邻
两箱的距离为L。每个箱子在A处投放后，在到达B之前已经相对于传送带静止，且以后也不再滑动（忽略经BC段时的微小滑动）。已知在一段相当长的时间T内，共运送小货箱的数目为N。这装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦。求电动机的平均输出功率P。
15（06全国Ⅰ）一水平的浅色长传送带上放置一煤块（可视为质点），煤块与传送带之间的动摩擦因数为。初始时，传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动。经过一段时间，煤块在传送带上留下了一段黑色痕迹后，煤块相对于传送带不再滑动。求此黑色痕迹的长度。
答案
1B 2BD 3.BD；4、ACD；5、（80J μ=0.25）
6、解：（1）旅行包做匀减速运动，
旅行包到达B端速度为
2分
包的落地点距B端的水平距离为
2分
（2）当时，皮带速度为
1分
当旅行包速度也为
时，在皮带上运动了位移
以后旅行包作匀速直线运动，所以旅行包到达B端的
|
2分
包的落地点距B端的水平距离为
（3）如图所示，每段图线2分。
7解：（1）设物体质量为m，在C点时运动速度为
，BC间距离为s。因物体恰在c点离开传送带，则
， 由动能定理，得
，联立得，
m/s，
m
（2）物体以最短时间到达C点，因此BC段物体以最大加速度做匀加速运动，设加速度为a，物体在B、C两点的速度分别为
、
，则
m/s2，
，
，
联立解得，
m/s，轮子转动的角速度
rad/s
（3）物体在BC段加速运动的时间为
s，
物体与皮带间相对位移为
m，
J
8、解：因
,所以工件在6s内先匀加速运动，后匀速运动，有
t1+t2=t, S1+S2=L
解上述四式得t1=2s,a=V/t1=1m/s2.
若要工件最短时间传送到B，工件加速度仍为a，设传送带速度为V，工件先加速后匀速，同上理有：
又因为t1=V/a,t2=t-t1,所以
，化简得：
,因为
，
所以当
,即
时，t有最小值，
。
表明工件一直加速到B所用时间最短。
9、解：(1) 
---①
---------------------------- ②
-------------------------------------------③
----⑤
物体先匀加速后匀速
-------------------------⑥
-------------------------------------⑦
评分标准：①④⑦各2分 ②③⑤⑥各1分 共10分
（2） 送一件物品电动机对传送带做的功 在数值上等于摩擦产生的热量和物品增加的机械能
-------------------------------①
--------------------- ②
解得： 
-------------------------------③
11解：物体放在传送带上后，开始阶段，传送带的速度大于物体的速度，传送带给物体一沿斜面向下的滑动摩擦力，物体由静止开始加速下滑，受力分析如图20（a）所示；当物体加速至与传送带速度相等时，由于μ＜tanθ，物体在重力作用下将继续加速，此后物体的速度大于传送带的速度，传送带给物体沿传送带向上的滑动摩擦力，但合力沿传送带向下，物体继续加速下滑，受力分析如图20(b)所示。综上可知，滑动摩擦力的方向在获得共同速度的瞬间发生了“突变” 。
开始阶段由牛顿第二定律得:ｍｇsinθ＋μｍｇcosθ=ｍa1;
所以:a1=ｇsinθ＋µｇcosθ=10m/s2;
物体加速至与传送带速度相等时需要的时间ｔ1＝ｖ／a1＝1s;发生的位移：
ｓ＝a1ｔ12/2＝5ｍ＜16ｍ;物体加速到10m/s 时仍未到达B点。
第二阶段，有：ｍｇsinθ－µｍｇcosθ＝ｍa2 ;所以：a2＝2m/s 2;设第二阶段物体滑动到B 的时间为t2 则：LAB－S＝ｖｔ2＋a２ｔ22/2 ；解得：t2＝1s , ｔ2/=-11s （舍去）。故物体经历的总时间ｔ=t1＋t 2 =2s .
从上述例题可以总结出，皮带传送物体所受摩擦力可能发生突变，不论是其大小的突变，还是其方向的突变，都发生在物体的速度与传送带速度相等的时刻。
12解析：（1）子弹击中木块的过程中，子弹与木块水平方向上动量守恒。
①
损失的机械能为△E 
②
（2）要使木块在传送带上发生相对运动时产生的热量最多，则需要木块滑到右端B处时，木块相对地面的速度为零，设木块击中后从A端运动到B端的时间为t1，则有：
0 ③ 
④
联解③、④得：
⑤
由①、⑤联解得：
木块被子弹击中后从A运动到B时速度为零，这个过程中相对皮带所发生位移S1为：
⑥
以后木块开始向左做匀加速运动，到停止滑动所经历的时间为t2，这段时间内木块相对皮带发生相对位移为S2，则有：
⑦
全过程中产生最大热量Q为：
13解：（1）解除锁定弹开AB过程中，机械能守恒有：
…………①
（2分）
取向右为正，动量守恒有：P前=P后，即0=mA(－VA)+mBVB…………② （2分）
由①②得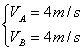
（2分）
B滑上皮带减速运动，设上滑距离为S，则由动能定理，W=△Ek有：
…………③
（2分）
（2分） 
（2分）
（2）物块B将沿皮带加速下滑，因
，当物块速度与皮带速度一致时一起匀速运动，到一起匀速运动下滑的距离
，有
……④
（2分）
（2分）
即刚好下滑至N处，B以
向左滑上水平面MN.
（3）设弹射装置给A做功为
，
…………⑤
（2分）
设AB碰后A的速度为
，B为
，则=………………⑥
B要滑上平台Q，由能量关系有：
. ⑦
……………………⑧
由⑤⑥⑦⑧得
（J） （2分）
14、设传送带的运动速度为v0，在水平段运输的过程中，小货箱先在滑动摩擦力作用下做匀加速运动，设这段路程为s，所用时间为t，加速度为a，则对小箱有
① 
② 在这段时间内，传送带运动的路程为
③ 由以上可得
④
用f表示小箱与传送带之间的滑动摩擦力，则传送带对小箱做功为
⑤
传送带克服小箱对它的摩擦力做功
⑥
两者之差就是克服摩擦力做功发出的热量 
⑦
可见，在小箱加速运动过程中，小箱获得的动能与发热量相等。 T时间内，电动机输出的功为 
⑧
此功用于增加小箱的动能、势能以及克服摩擦力发热，即
⑨
已知相邻两小箱的距离为L，所以 
⑩
联立⑦⑧⑨⑩，得
⑾