第八章 电路
第一节 电流概念、电阻定律、欧姆定律
一.本节高考考点及要求
1.欧姆定律 II
2.电阻定律 I
二.基础回顾
1.电流
电流的定义式:![]() ,适用于任何电荷的定向移动形成的电流。
,适用于任何电荷的定向移动形成的电流。
2.电阻定律
导体的电阻R跟它的长度l成正比,跟它的横截面积S成反比。![]()
⑴ρ是反映材料导电性能的物理量,叫材料的电阻率。单位是Ωžm。
⑵纯金属的电阻率小,合金的电阻率大。
⑶材料的电阻率与温度有关系:
①金属的电阻率随温度的升高而增大。铂较明显,可用于做温度计;锰铜、镍铜的电阻率几乎不随温度而变,可用于做标准电阻。
②半导体的电阻率随温度的升高而减小。
③有些物质当温度接近0 K时,电阻率突然减小到零——这种现象叫超导现象。能够发生超导现象的物体叫超导体。
3.欧姆定律
![]() (适用于金属导体和电解液,不适用于气体导电)。
(适用于金属导体和电解液,不适用于气体导电)。
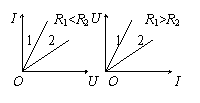
电阻的伏安特性曲线:注意I-U曲线和U-I曲线的区别。若材料的电阻率随温度而变化,则电阻的伏安特性曲线不再是过原点的直线。
三.例题精讲
例1. 氢原子的核外只有一个电子,设电子在离原子核距离为R的圆轨道上做匀速圆周运动.已知电子的电荷量为e,运动速率为v,求电子绕核运动的等效电流多大?
解析:取电子运动轨道上任一截面,在电子运动一周的时间T内,通过这个截面的电量q=e,由圆周运动的知识有:
T=![]()
根据电流的定义式得:
I=![]()
 例2.
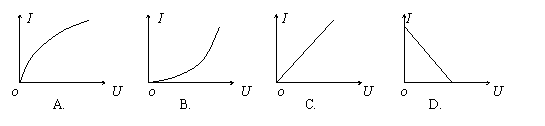
实验室用的小灯泡灯丝的I-U特性曲线可用以下哪个图象来表示:
例2.
实验室用的小灯泡灯丝的I-U特性曲线可用以下哪个图象来表示:
分析:灯丝在通电后一定会发热,当温度达到一定值时才会发光,因此必须考虑到灯丝的电阻将随温度的变化。电压的升高时,电流增大,灯丝电功率增大,温度升高,电阻率随之增大,导致电阻增大。因此U越大,I-U曲线上对应点与原点连线的斜率必然越小,答案选A。
例3.如图所示,两段材料相同、长度相等、但横截面积不等的导体接在电路中,总电压为U,则 (ACD)
A.通过两段导体的电流相等
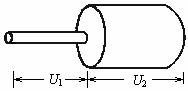 B.细导体两端的电压U1与粗导体两端的电压U2相等
B.细导体两端的电压U1与粗导体两端的电压U2相等
C.细导体两端的电压U1大于粗导体两端的电压U2
D.细导体内的电场强度大于粗导体内的电场强度
分析:粗、细导体串联在电路中电流相等,答案A对;又细导体电阻R1大于粗导体R2,则U1> U2;再由![]() 可以得出细导体中电场大于粗导体中电场,故答案ACD正确。
可以得出细导体中电场大于粗导体中电场,故答案ACD正确。
 例4.如图所示,a、b、c、d是滑动变阻器的4个接线柱,现把此滑动变阻器串联接入电路中,并要求滑片P向接线柱c移动时,电路中的电流减少,则接入电路的接线柱可能是( )
例4.如图所示,a、b、c、d是滑动变阻器的4个接线柱,现把此滑动变阻器串联接入电路中,并要求滑片P向接线柱c移动时,电路中的电流减少,则接入电路的接线柱可能是( )
A. a和b B. a和c
C. b和c D. b和d
分析:要使滑片P滑动时电流减少,则P向C滑动时变阻器接入的电阻应不断增大,由此可以得出CD正确。
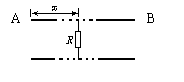 例5.如图所示,AB两地间铺有通迅电缆,长为L,它是由两条并在一起彼此绝缘的均匀导线组成的,通常称为双线电缆。在一次事故中经检查断定是电缆上某处的绝缘保护层损坏,导致两导线之间漏电,相当于该处电缆的两导线之间接了一个电阻。检查人员经过下面的测量可以确定损坏处的位置:
例5.如图所示,AB两地间铺有通迅电缆,长为L,它是由两条并在一起彼此绝缘的均匀导线组成的,通常称为双线电缆。在一次事故中经检查断定是电缆上某处的绝缘保护层损坏,导致两导线之间漏电,相当于该处电缆的两导线之间接了一个电阻。检查人员经过下面的测量可以确定损坏处的位置:
(1)令B端的双线断开,在A处测出双线两端间的电阻RA;(2)令A端的双线断开,在B处测出双线两端的电阻RB;(3)在A端双线间加一已知电压UA,在B端用内阻很大的电压表测出两线间的电压UB。试由以上测量结果确定损坏处的位置。
【解析】设双线电缆单位长度的电阻为r , 漏电处电阻为R,漏电处距A端为x,则
![]()
![]()
由欧姆定律可知,![]()
解得 ![]()
四.跟踪练习
1.关于电阻率,下列说法中不正确的是
A.电阻率是表征材料导电性能好坏的物理量,电阻率越大,其导电性能越好
B.各种材料的电阻率都与温度有关,金属的电阻率随温度升高而增大
C.所谓超导体,当其温度降低到接近绝对零度的某个临界温度时,它的电阻率突然变为零
D.某些合金的电阻率几乎不受温度变化的影响,通常都用它们制作标准电阻
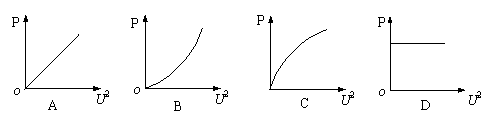
2.下图所列的4个图象中,最能正确地表示家庭常用的白炽电灯在不同电压下消耗的电功率P与电压平方U 2之间的函数关系的是以下哪个图象
 3.如图所示,a、b、c、d是滑动变阻器的4个接线柱,现把此变阻器串联接入电路中并要求滑片P向接线柱d移动时,电路中的电流增大,则接入电路的接线柱可能是
3.如图所示,a、b、c、d是滑动变阻器的4个接线柱,现把此变阻器串联接入电路中并要求滑片P向接线柱d移动时,电路中的电流增大,则接入电路的接线柱可能是
A.a和c B. b和c
C. a和d D.b和d
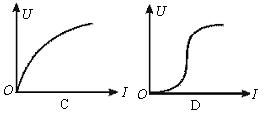
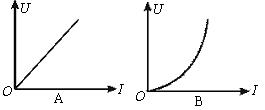 4.一个标有“220 V、60W”的白炽灯泡,加上的电压U由零逐渐增大到220 V,在此过程中,电压(U)和电流(I)的关系可用图象表示,题中给出的四个图线中,肯定不符合实际的是
4.一个标有“220 V、60W”的白炽灯泡,加上的电压U由零逐渐增大到220 V,在此过程中,电压(U)和电流(I)的关系可用图象表示,题中给出的四个图线中,肯定不符合实际的是
5.一根粗细均匀的导线,两端加上电压U时,通过导线中的电流强度为I,若将导线均匀拉长,使其半径变为原来的![]() ,再给它两端加上电压U,则
,再给它两端加上电压U,则
A.通过导线的电流为![]() B.通过导线的电流为
B.通过导线的电流为![]()
C. 通过导线的电流为![]() D. 通过导线的电流为
D. 通过导线的电流为![]()
6.一个阻值为R=20欧的电阻与多个未知电阻连接后组成如图所示电路,此时A、B两端加上6.0伏电压,安培表示数为0.6安培,若将电阻R改为30欧,A、B两端所加电压仍为6.0则此时安培表的示数应为
 A.0.3 A B.0.4 A
A.0.3 A B.0.4 A
C.0.5A D. 0.6 A
7.若加在导体两端的电压变为原来的![]() 时,导体中的电流减小0.2 A,如果所加电压变为原来的2倍,则导体中的电流将变为_______.
时,导体中的电流减小0.2 A,如果所加电压变为原来的2倍,则导体中的电流将变为_______.
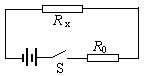 8.如图所示,电源可提供U=6 V的恒定电压,R0为定值电阻,某同学实验时误将一电流表(内阻忽略)并联于Rx两端,其示数为2 A,当将电流表换成电压表(内阻无限大)后,示数为3 V,则Rx的阻值为_______Ω.
8.如图所示,电源可提供U=6 V的恒定电压,R0为定值电阻,某同学实验时误将一电流表(内阻忽略)并联于Rx两端,其示数为2 A,当将电流表换成电压表(内阻无限大)后,示数为3 V,则Rx的阻值为_______Ω.
 9.将阻值为16 Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图1—28—8所示,要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是______________.
9.将阻值为16 Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图1—28—8所示,要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是______________.
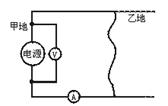 10.甲、乙两地相距6 km,两地间架设两条电阻都是6 Ω的导线.当两条导线在甲、乙两地间的某处发生短路时,接在甲地的电压表,如图所示,读数为6 V,电流表的读数为1.2 A,则发生短路处距甲地多远?
10.甲、乙两地相距6 km,两地间架设两条电阻都是6 Ω的导线.当两条导线在甲、乙两地间的某处发生短路时,接在甲地的电压表,如图所示,读数为6 V,电流表的读数为1.2 A,则发生短路处距甲地多远?
11.某用电器离电源L,线路上电流为I,若要求线路上电压不超过U,输电线电阻率为ρ,则该输电线的横截面积需满足什么条件?
 12.如图所示是一种悬球式加速度仪.它可以用来测定沿水平轨道做匀加速直线运动的列车的加速度。m是一个金属球,它系在细金属丝的下端,金属丝的上端悬挂在O点,AB是一根长为l的电阻丝,其阻值为R。金属丝与电阻丝接触良好,摩擦不计。电阻丝的中点C焊接一根导线.从O点也引出一根导线,两线之间接入一个电压表V (金属丝和导线电阻不计).图中虚线OC为竖直线,且OC=h,电阻丝AB接在电压恒为U的直流稳压电源上.整个装置固定在列车中,AB沿着车前进的方向。当列车加速或减速前进时,金属线将偏离竖直方向的角度为θ,从电压表的读数变化可以测出加速度的大小。
12.如图所示是一种悬球式加速度仪.它可以用来测定沿水平轨道做匀加速直线运动的列车的加速度。m是一个金属球,它系在细金属丝的下端,金属丝的上端悬挂在O点,AB是一根长为l的电阻丝,其阻值为R。金属丝与电阻丝接触良好,摩擦不计。电阻丝的中点C焊接一根导线.从O点也引出一根导线,两线之间接入一个电压表V (金属丝和导线电阻不计).图中虚线OC为竖直线,且OC=h,电阻丝AB接在电压恒为U的直流稳压电源上.整个装置固定在列车中,AB沿着车前进的方向。当列车加速或减速前进时,金属线将偏离竖直方向的角度为θ,从电压表的读数变化可以测出加速度的大小。
(1)当列车向右做匀加速直线运动时,试写出加速度a与θ角的关系及加速度a与电压表读数U′的对应关系.
(2)这个装置能测得的最大加速度是多少?
五.参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| B | C | BD | ACD | D | C | 1.2 A | 3 |
9.π;![]() 或
或![]() π.圆形滑动变阻器Q、P之间的电阻为两段圆弧的电阻R1、R2并联所得的总电阻,找出总电阻与θ关系即可求解.
π.圆形滑动变阻器Q、P之间的电阻为两段圆弧的电阻R1、R2并联所得的总电阻,找出总电阻与θ关系即可求解.
10.2.5 km 11.S≥![]()
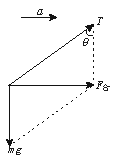
12.(1)小球受力如图所示,由牛顿定律得:a=![]() =
=![]() =gtanθ.设细金属丝与竖直方向夹角为θ时,其与电阻丝交点为D,CD间的电压为U′,则
=gtanθ.设细金属丝与竖直方向夹角为θ时,其与电阻丝交点为D,CD间的电压为U′,则![]() ,故得a=gtanθ=g·
,故得a=gtanθ=g·![]() .(2)因CD间的电压最大值为U/2,即Umax′=U/2,所以amax=
.(2)因CD间的电压最大值为U/2,即Umax′=U/2,所以amax=![]() g.
g.