模拟试卷36
一、填空题:
![]()
a×b=______,a÷b______.
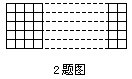
2.用长短相同的火柴棍摆成5×1997的方格网,每一个小方格的边长为一根火柴棍长(如图),共需用______根火柴棍.
![]()
要分别装入小瓶并无剩余,并且每瓶重量相等,照这种装法,最少要用______个瓶子.
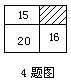
4.一块长方形耕地如图所示,已知其中三块小长方形的面积分别是15、16、20亩,则阴影部分的面积是______亩.
5.现有大小油桶40个,每个大桶可装油5千克,每个小桶可装油3千克,大桶比小桶共多装油24千克,那么,大油桶一个,小油桶______个.
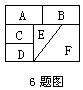
6.如图,把A,B,C,D,E,F这六个部分用5种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色,那么这幅图一共有______种不同的着色方法.
7.“12…282930”是一个多位数,从中划去40个数字,使剩下的数字(先后顺序不能变)组成最大的多位数,这个最大的多位数是______.
8.一水库存水量一定,河水均匀流入水库内.5台抽水机连续抽10天可以抽干;6台同样的抽水机连续抽8天可以抽干。若要求4天抽干,需要同样的抽水机______台.
9.如图,A、C两地相距3千米,C、B两地相距8千米.甲、乙两人同时从C地出发,甲向A地走,乙向B地走,并且到达这两地又都立即返回.如果乙的速度是甲的速度的2倍,那么当甲到达D地时,还未能与乙相遇,他们相距1千米,这时乙距D地______千米.
![]()
10.一次足球赛,有A、B、C、D四队参加,每两队都赛一场.按规则,胜一场得2分,平一场得1分,负一场得0分.比赛结果,C队得5分,A队得3分,D队得1分,所有场次共进了9个球,C队进球最多,进了4个球,A队共失了3个球,B队一个球也没进,D队与A队比分是2∶3,则D队与C队的比分是______.
二、解答题:
1.一个人以相同的速度在小路上散步,从第1棵树走到第13棵树用了18分,如果这个人走了24分,应走到第几棵树?
2.在黑板上写出3个整数分别是1,3,5,然后擦去一个换成其它两数之和,这样操作下去,最后能否得到57,64,108?为什么?
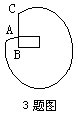
3.有一根6厘米长的绳子,它的一端固定在长是2厘米、宽是1厘米的长方形的一个顶点A处(如图),让绳子另一端C与边AB在一条线上,然后把它按顺时针方向绕长方形一周,绳子扫过的面积是多少?
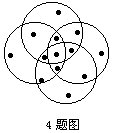
4.如图,四个圆相互交叉,它们把四个圆面分成13个区域.如果在这些区域上(加点的)分别填上6至18的自然数,然后把每个圆中的数各自分别相加,最后把这四个圆的和相加得总和,那么总和最大可能是多少?
模拟试卷36
一、填空题:
![]()
a÷b=1.5.
2.21972
横放需1997×6根,竖放需1998×5根,共需:
1997×6+1998×5
=1997×(6+ 5)+ 5
=21972(根)
3.129

![]()
9的公约数,为了使装瓶数尽可能少,a取15、42、9的最大公约数![]()
少要用的瓶数:
![]()
=50+64+15
=129(瓶)
4.12
设阴影面积的长为a,宽为b,则面积为20亩的耕地的长与宽可以分别![]()
a×b=15×16÷20=12(亩)
5.大油桶18个,小油桶22个.
假设40个油桶都是大桶,则共装油200千克,而小桶装油0千克,大桶比小桶共多装油200千克,比条件给的差数多了200-24=176千克,多的原因是把小桶看成了大桶.若把40个大桶中的一部分换成小桶,则每把一个大桶换成一个小桶,大桶装油总数就减少了5千克,小桶装油就增加了3千克,所以大桶比小桶多装的千克数就减少了5+3=8千克,那么需要把多少个大桶换成小桶呢?列式为
(5×4-24)÷(5+3)=22(2个)……小桶个数
40-22=18(个)……大桶个数.
6.960
对于A有5种着色方法,B与A相邻,有4种着色方法;C与A相邻,它可以与B的颜色相同,因此C有4种着色方法;同理可以知D有4种着色方法,E有1 种着色方法,F有3种着色方法,共有:
5×4×4×4×1×3= 960(种)
7.
这个多位数共有9+21×2=51位数字,划去40个数字,还有11个数字.在划去数字时,前面尽可能多的留下9,才能保证剩下的数字最大,这个多位数只有3个9,所求数只能前两位是9,这时多位数还剩202122…282930这些数字,还要再留下9个数字,这时可以从后往前考虑,留下.所求最大数为 .
8.11

从上图可以看出5台抽水机10天抽水量与6台抽水机8天抽水量的差恰好是10- 8= 2天流入的水量,如果设一台抽水机一天抽水量为1份,可以求出河水每天流入水库的水量为:
(5×10-6×8)÷(10-8)=1(份)
水库原有水量为:
5×10-1×10=40(份)
4天抽干水库需要抽水机台数:
(40+1×4)÷4=11(台)
9.2
设CD两地相距x千米,则甲从C出发到A再返回到D,共行了(3×2+x)千米,乙从C出发到B再返回距D地1千米处,共行了(8×2-x-1)千米,由于乙速是甲速的2倍,所以相同时间里乙行的距离是甲行距离的2倍,因此有
(3×2+x)×2=8×2-x-1
12+2x=15-x
x=1(千米)
这时乙距C地2千米.
10.0∶3
四个队每两队都赛一场,共赛6场,每一场两队得分之和是2分,因此所有队在各场得分之和是2×6=12分.B队得分为:
12-5-3-1=3(分)
由于B队一个球没进,又得3分,必是与其他三队比赛时打平.现将比赛情况列表如下:

C队得5分,必是胜2场平1场,D队得1分,必是平1场,负2场,D队与A队比分是2∶3,A队必是胜1场平1场负1场.D队与A队比赛时, A队进了3个球, D队进了2个球,这一场共进了5个球,C队进球数是4,合起来共9个球,因而A、D两队只在A、D两队比赛中进了球,而在其他场比赛没进球.
C队与B队比分是0∶0,C队进的4个球必是与A队或D队比赛时进的.因为A队失3个球,在与D队比赛时失了2个球,因此与C队比赛时失1个球,这样A队与C队比分是0∶1,于是在C队与D队比赛中,C队进了3个球,D队没有进球,所以D队与C队比分是0∶3.
二、解答题:
1.这个人应走到第17棵树.
从第1棵走到段13棵树,共走了12个间段,用了18分钟,每段所用时![]()
这个人应走到第17棵树.
2.不能
由于一开始是1、3、5,这三个均是奇数,擦去任意一个,改为剩下两个奇数之和应是偶数,这样三个数是两个奇数一个偶数,以后如果擦掉是偶数,换上的是偶数,擦去一个奇数,换上的必是奇数,因而永远是两个奇数一个偶数,但是57、64、108是一个奇数两个偶数,所以无论如何无法得到这三个数.
3.15.5π或 48. 7平方厘米
![]()
![]()
分别是6、4、3、1厘米,故绳子扫过的面积为:

![]()
4.380
经过观察发现,图中13个区域可以分成四种情况;第一种是四个圆的公共部分,第二种是三个圆的公共部分,第三种是二个圆的公共部分,第四种是一个圆单独的部分.由于题目要求总和最大,第一种区域求和时要用4次,所以把最大数18放在第一种区域,同理第二种区域分别放上17、16、15、14,第三种区域分别放上13、12、11、10,剩下4个数分别放在第四种区域,这样得总和最大值是:
18×4+(17+16+15+14)×3+(13+12+11+10)×2+9+8+7+6=380