四 数阵
1.在下列各图中,将从1开始的连续自然数填入图中的○内,要求每边上的数字之和都相等,中心○处各有几种填法?(每小题给出一个解)
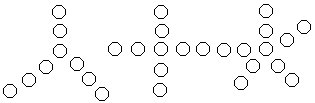
2.将1~11填入左下图的○内,使每条虚线上的三数之和都等于18。
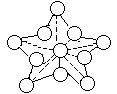
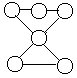
3.将1~6填入右上图的○中,要求四条直线上的数字之和都等于10。
4.将1~6填入左下图的六个○中,使三角形每条边上的三个数之和都等于k,请指出k的取值范围。
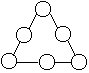
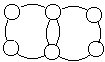
5.将1~6填入右上图的六个○中,使每个大圆周上的四数之和都等于16。
6.将1~9这九个自然数分别填入左下图中的九个○内,使三角形每边上的四数之和都等于20,且有一个顶点○内的数字为1。

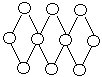
7.将1~10填入右上图的10个○中,使得每个菱形的4个顶点数之和都等于定数k。问:k的最大值与最小值各是多少?请各给出一种填法。
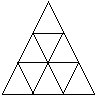
8.将1~9这九个自然数填入左下图的九个小三角形中,使得每个由四个小三角形构成的三角形内的四个数字之和都等于17。
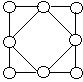
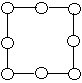
9.将1~8这八个自然数分别填入右上图中的八个○内,使四边形每条边上的三数之和都相等且尽可能大。
10.将自然数1~8填在右图的八个○内,使每个小三角形三个顶点数字之和都等于13,并且8位于大正方形的一个顶点上。
11.将1~8这八个自然数填入右图的四个圆相互分割的八个部分中,使每个圆内的三个数字之和都相等,并且这个和尽量小。
12.将自然数1~10这10个自然数分别填入左下图的10个○内,使五边形每条边上的3数之和都等于17,并且数字1位于一个顶点上。
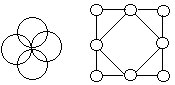
13.将1~8填入右上图的八个○中,使小正方形的四个顶点数之和是大正方形的四个顶点数之和的两倍,并且大正方形每条边上的三个数之和都相等。
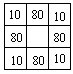
14.小明玩布阵游戏,他要用360名士兵守卫一座城池(见左下图,图中间表示城区,四周表示城墙,方格中的数表示兵力分布),要求四个角的兵力相同。现在的兵力分布恰好每边有100名士兵,如果小明想使每边有150名士兵,那么兵力应如何分布?
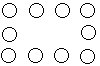
15.有座一长方形城堡,四周有10个掩体(如右上图)。守城的士兵有10件武器,各种武器的威力系数如下表。为了使每一面的武器威力系数都相同,并且尽量大,应如何在10个掩体中配备武器?

16.将1~5填入右图的○中,使得横、竖、大圆周上的几个数之和都相等。
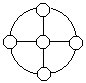
17.将1~7七个数字填入左下图的七个○内,使每个圆周和每条直线上的三个数之和都相等。
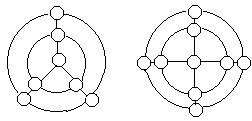
18.将1~8八个数字填入右上图的八个○内,使每个圆周和每条直线上的四数之和都相等。
19.将1~10填入左下图的10个○内,使3条直线上的4个数字之和相等,3个正三角形3个顶点上的数字之和也相等。
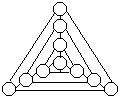
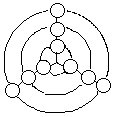
20.将1~9填入右上图的九个○内,使得每个圆周和每条直线上的三数之和都相等,并且7,8,9依次位于小、中、大圆周上。
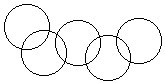
21.左下图是大家都熟悉的奥林匹克的五环标志。请将1~9分别填入五个圆相互分割的九个部分,并且使每个圆环内的数字之和都相等。
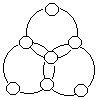
22.将1~7这七个自然数分别填入右上图的七个○内,使得三个大圆周上的四个数之和都等于定数,指出这个定数所有的可能取值,并给出定数为13时的一种填法。
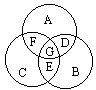
23.将1~7分别填入下右图中的A,B,C,D,E,F,G七个部分,使每个圆内的四个数字之和都等于14,并要求G部分填的是奇数。
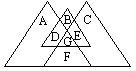
24.将1~7填入右图中的A,B,C,D,E,F,G七个部分,使每个内含四个数的三角形内的四个数之和都等于19。
25.将1~9填入左下图的九个○内,使四个大圆周上的四数之和都等于定数16。
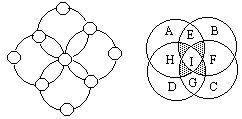
26.右上图中的四个圆除阴影部分外被相互分割成A,B,C,D,E,F,G,H,I九个部分,将1~9这九个自然数分别填入这九个部分,使每个圆内的四个数字之和都等于20,并要求I部分填入奇数。
27.右图中有5个正方形和12个圆圈,将1~12填入圆圈中,使得每个正方形四角上圆圈中的数字之和都等于K,那么K等于几?
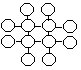
28.下面各图中各有10个小三角形和4个大三角形,将1~10填入每个小三角形,使每个大三角形内的数字之和都等于25(其中已填好了3个数):
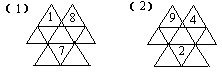
29.将1~9填入下列各图的九个○中(其中6和1已填好),使得每个三角形上的三个数之和都相等:
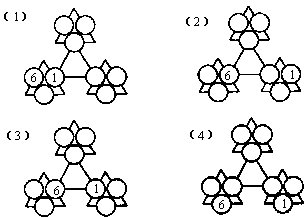
30.下图的大三角形被分割成九个小三角形,大三角形的每条边都与其中五个小三角形有公共点。如果将1~9分别填入这九个小三角形,使得每条边上的五个小三角形内的数字之和都相等,那么这个和的最小值是多少?最大值是多少?
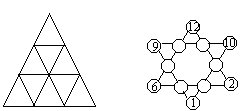
31.自然数1~12中有些已填入右上图的○内,请将其余的数补充填入,使得每条直线上的四数之和都相等。
32.将1~9填入下图的九个○内,使每个圆周上的四数之和都相等。
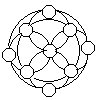
33.下图中有6个正方形,将1~9填入图中的9个○内,使得每个正方形4个顶点上的数字之和都相等。
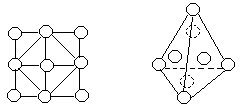
34.将数字1~8分别填入右上图所示四面体的八个○中,使每个面上的四个○中的数字之和都等于14。
35.将数字1~8标在下图所示立方体的八个顶点上,使得每个面上的四个顶点所标数字之和相等。
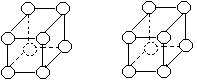
36.在上图所示立方体的八个顶点上标出1~9中的八个,使得每个面上四个顶点所标数字之和都等于k,并且k不能被未标出的数整除。
37.将1~8填入下图所示立方体的八个顶点上,其中1已经填好,要使任意相邻的两条棱上的三个数之和都是两位数,A处应填几?
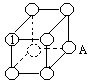
38.下页上图中有三个正三角形,将1~9填入它们顶点处的九个○中,要求每个正三角形顶点的三数之和都相等,并且通过四个○的每条直线上的四数之和也相等。

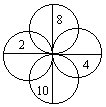
39.将1~12填入右上图的空格中(其中已填好四个数),使每个圆内的四个数之和都等于28。
40.将九个连续自然数填入左下图的九个空格中,使每一横行和每一竖列的三数之和都等于60。
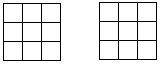
41.将从1开始的九个连续奇数填入右上图的九个空格中,使每一横行、每一竖列及每条对角线上的三个数之和都相等。
42.将九个数填入左下图的九个空格中,使得任一行、任一列以及任一条对角线上的三个数之和都等于定数k。
![]()
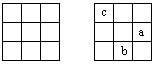
43.将九个数填入右上图的空格中,使得每行、每列以及每条对角线上
![]()
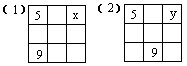
44.下列各图中的九个小方格内各有一个数字,而且每行、每列及每条对角线上的三个数之和都相等,求x和y。
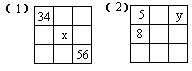
45.下列各图中九个小方格内各有一个数字,而且每行、每列及每条对角线上的三个数之和都等于24,求x和y。
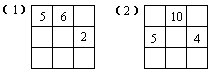
46.下列各图中的九个小方格内各有一个数字,而且每行、每列及每条对角线上的三个数之和都相等,求x和y。
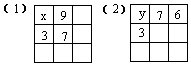
47求任一列、任一行以及任一条对角线上的三个数之和都等于267的三阶质数幻方。
48.求九个数之和为531的三阶质数幻方。
49.求四个角上的四个数字之和为292的三阶质数幻方。
50.在下列各图的每个方格中都填入一个数字,使得每行、每列以及每条对角线上的四个数字都是1,2,3,4。
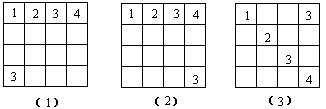
51.在下列各图的空格中填入不大于12且互不相同的九个自然数(已填好一个),使每一横行、竖行及对角线上的三数之和都等于21。
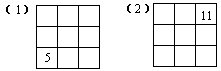
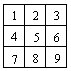
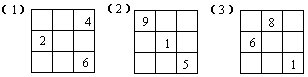
52.下图的九个小方格中填的数正好是1~9,并且满足:既不同行也不同列的任意三个数之和都等于15。符合题意的不同填法共有36种。下面各小题中都已填上了三个数,请将其余的数补上。
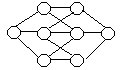
53.将1~8填入右图中的○内,要求按照自然数顺序相邻的两个数不能填入有直线段连接的相邻的两个○内。
54.将1~8填入右图的八个空格,使得横、竖、对角任何两个相邻空格中的数不是连续数。
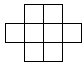
55.下图的九个○由线段相连,其中一个○里的数是6。请选出九个连续自然数(包括6在内)填入○中,使每条直线上的各数之和都等于23。
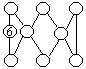
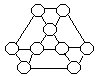
56.将1~9填入右上图中的九个○内,使图中所有三角形(共七个)的三个顶点数之和都相等。
57.将自然数1~11填入下图的11个○中,使得每条直线(共10条)上的三个数字之和都相等。
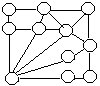
58.在下图的六个○内各填入一个质数,使它们的和等于20,且每个三角形(共五个)的三个顶点数之和相等。
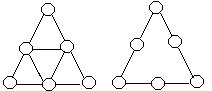
59.将1,2,3,4,8,12这六个数填入右上图的六个○内,使三角形每条边上的三个数的乘积都相等。
60.在下图的七个○内各填入一个质数,使每个小三角形(共六个)的三个顶点数之和相等,且为尽量小的质数。
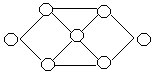
61.把20以内的质数分别填入左下图中的八个○,使图中用箭头连接起来的四个数之和都相等。
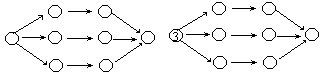
62.20以内共有10个奇数,去掉9和15还剩八个奇数,将这八个奇数填入上图的八个○中(其中3已填好),使得用箭头连接起来的四个数之和都相等。
63.在图的空格中任意填入八个自然数(可以相同),使每边的数字之和为5,而八个数的总和为12。如果八个数的总和为13,14,15,16呢?
64.从1~13中选出12个自然数填入左下图的空格中,使每横行四数之和相等,每竖列三数之和也相等。
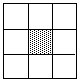
65.将1~6分别填入右上图的六个○中,使得每个三角形三个顶点的数字之积能被它的三个顶点的数字之和整除,并且正方形四个顶点的数字之积也能被它的四个顶点的数字之和整除。
66.将1~9填入下图的九个○中,使得三角形每条边(共有六条)上的三个数之和都相等。
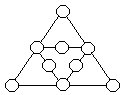
67.在下列各图的九个方格中已填入四个数,请再填入五个自然数,使得任一行、任一列的三个数之积都相等:
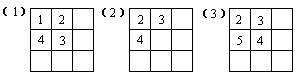
68.在下列各图中分别填入五个自然数,使得每一横行、每一竖列的三个数的乘积都相等:
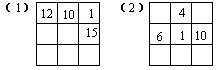
69.在下列各图中分别填入六个自然数,使得每一横行、每一竖列的三个数的乘积都等于60:
70.右图的四个圆被相互分割成八个部分,在这八个部分中分别填入1或2,使得各圆内的三个数字之和互不相同。
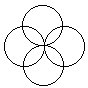
71.在下图的六个○内填入1或2,使得每个大圆周上的四个数字之和互不相同。
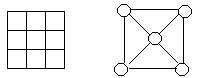
72.将前9个自然数填入左下图的9个方格中,使得任一行、任一列以及任一条对角线上的3个数之和互不相同,并且相邻的2个自然数在图中的位置也相邻。
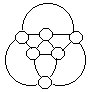
73.在右上图的五个○内各填入一个自然数,使得图中八个三角形的顶点数字之和互不相同。满足这个条件的自然数有很多组,求所填五个数之和最小的一组。
74.下图中有三个正方形,在每个正方形的四个顶点上填入1,2,3,4四个数。问:
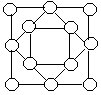
(1)能否使八个三角形顶点数之和都相等?
(2)能否使八个三角形顶点数之和互不相同?如果能,请画图填数;如果不能,请说明理由。