1998小学数学奥林匹克试题
预赛(A)卷
1.计算：
=________。
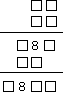
2.在左下图的乘法算式中，每个□表示一个数字，那么计算所得的乘积应该是________。
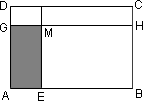
3.在右上图中，已知矩形GHCD的面积是矩形ABCD面积的
，矩形MHCF的面积是矩形ABCD面积的
，矩形BCFE的面积等于3平方米。矩形AEMG的面积等于________平方米。
4.三个连续的自然数的最小公倍数是9828，这三个自然数的和等于________。
5.如果四个两位质数a、b、c、d两两不同，并且满足等式a+b=c+d,那么a+b的最大可能值是________。
6.某数除以11余8，除以13余10，除以17余12,那么这个数的最小可能值是________。
7.一个长方体，表面全涂上红色后，被分割成若干个体积都等于1立方厘米的小正方体。如果在这些小正方体中，不带红色的小正方体的个数等于7，那么两面带红色的小正方体的个数等于________。
8.甲、乙两个车间共有94个工人，每天共生产1998把竹椅。由于设备和技术的不同，甲车间平均每个工人每天只生产15把竹椅，而乙车间平均每个工人每天可以生产43把竹椅。甲车间每天竹椅的产量比乙车间多________把。
9.一个运输队包运1998套玻璃茶具。运输合同规定：每套运费以1.6元计算，每损坏一套，不仅不得运费，还要从总费中扣除赔偿费18元。结果这个队实际得运费3059.6元。在运输过程中被损坏的茶具套数是________。
10.买来一批苹果，分给幼儿园大班的小朋友。如果每人分5个苹果，那么还剩余32个；如果每人分8个苹果，那么还有5个小朋友分不到苹果。这批苹果的个数是________。
11.某司机开车从A城到B城。如果按原定速度前进，可准时到达。当路程走了一半时，司机发现前一半路程中，实际平均速度只可达到原定速度的
。现在司机想准时到达B城，在后一半的行程中，实际平均速度与原速度的比是_______。
12.某店原来将一批苹果按100％的利润定价出售，由于定价过高，无人购买，不得不按38％的利润重新定价，这样售出了其中的40％。此时，因害怕剩余水果腐烂变质，不得不再次降价，售出了剩余的全部水果。结果，实际获得的总利润是原定利润的30.2%，那么第二次降价后的价格是原定价格的______％。（注：“按100％的利润定价”指的是“利润＝成本×100％”）
预赛(B)卷
1.计算：
＝________。
2.在下图的乘法算式中，每个□表示一个数字，那么计算所得的乘积应该是________。
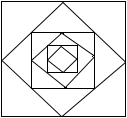
3.右上图中有六个正方形，较小的正方形都由较大的正方形的四边中点连接而成。已知最大的正方形的边长为10cm,那么最小的正方形的面积等于________cm2。
4.三个连续的自然数的最小公倍数168，那么这三个自然数的和等于________。
5.如果四个两位质数a、b、c、d两两不同，并且满足等式a+b=c+d,那么a+b的最小可能值是________。
6.一个小于200的数，它除以11余8，除以13余10,那么这个数是________。
7.一个长方体的长、宽、高都是整数厘米，它的体积是1998立方厘米，那么它的长、宽、高的和的最小可能值是________厘米。
8.甲、乙两箱红枣，每箱内装1998颗，如果从乙箱中拿出若干颗红枣放入甲箱后，甲箱的红枣颗数恰好比乙箱多40%，那么，从乙箱拿到甲箱________颗红枣。
9.某玩具店第一天卖出玩具小狗98个，每个获利44元1角；第二天卖出玩具小狗133个，获得的利润是成本的40%。已知第一天卖玩具小狗所得的钱数和第二天所得的一样多，那么每个玩具小狗的成本是________。
10.幼儿园大班和中班共有32个男生，18个女生。已知大班中男生数与女生数的比为5:3，中班中男生数与女生数的比为2:1，那么大班的女生数等于________。
11.甲班有42名学生，乙班有48名学生。已知在某次数学考试中按百分制评卷，评卷的结果各班的数学总成绩相同，各班的平均成绩都是整数，并且平均成绩都高于80分，那么甲班的平均成绩比乙班高________。
12.乐乐放学回家需走10分钟，晶晶放学回家需走14分钟。已知晶晶回家的路程比乐乐回家的路程多
，乐乐每分钟比晶晶多走12米，那么晶晶回家的路程是________米。
决赛(A)卷
1.已知等式
，式中□内应填的数是________。
2.左下图是一个算式，每个□内填一个数字，这个算式中的乘积应该是________。
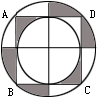
3.已知正方形ABCD的边长为10厘米，过它的四个顶点做一个大圆，过它的各边中点做一个小圆，再将对边中点用直线连接起来得右上图。那么阴影部分的总面积等于________平方厘米。（注：π取3.14）
4.由1、2、3、4、5五个数字组成的五位数共有120个，将它们从小到大排列起来，第95个数等于________。
| 5.已知两个大于1的数互质，它们的和是5的倍数，它们的积是2924，那么它们的差等于________。 6.如右图，正方形ACEG的边界上共有7个点A、B、C、D、 E、F、G,其中B、D、F分别在边AC、CE、EG上。以这7点中的4个点为顶点组成的不同的四边形的个数等于________。 7.在从1到1998的自然数中，能被2整除，但不能被3或7整除的数的个数等于________。 |
|
8.小赵的电话号码是一个五位数，它由五个不同的数字组成。小王说：“它是93715。”小张说：“它是79538。”小李说：“它是15239。”小赵说：“谁说的某一位上的数字与我的电话号码上的同一位数字相同，就算谁猜对了这个数字。现在你们三人猜对的数字个数都一样，并且电话号码上的每个数字都有人猜对。而每个人猜对的数字的位数都不相邻。”这个电话号码是________。
9.某商品按原定价出售，每件利润为成本的25%，后来按原定价的90%出售，结果每天售出的件数比降价前增加了1.5倍，每天经营这种商品的总利润比降价前增加了________%
10.甲火车4分钟行进的路程等于乙火车5分钟行进的路程。乙火车上午8：00从B站开往A站，开出若干分钟以后，甲火车A站出发开往B站。上午9：00两列火车相遇，相遇的地点离A、B两站的距离的比是15:16，那么，甲火车从A站发车的时间是______点______分。
11.一群猴子采摘水蜜桃。猴王不在的时候，一个大猴子一小时可采摘15千克，一个小猴子一小时可采摘11千克；猴王在场监督的时候，大猴子的
和小猴子的必须停止采摘，去伺候猴王。有一天，采摘了8小时，其中只有第一小时和最后一小时有猴王在场监督，结果共采摘3382千克水密桃。在这个猴群中，共有大猴子________只。
12.某次数学竞赛设一、二、三等奖。已知：
(1)甲、乙两校获一等奖的人数相等；
(2)甲校获一等奖的人数占该校获奖总人数的百分数与乙校相应的百分数的比为5：6；
(3)甲、乙两校获二等奖的人数总和占两校获奖人数总和的20％；
(4)甲校获三等奖的人数占该校获奖人数的50％；
(5)甲校获二等奖的人数是乙校获二等奖人数的4.5倍。
那么，乙校获一等奖的人数占该校人数的百分数等于________。
决赛(B)赛
1.已知等式
式中所表示的数是________。
2.左下图是一个乘法算式，每个□内填一个数字，这个算式中的乘积应该是________。
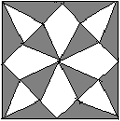
3.右上图中，大正方形的边长为10厘米。连接大正方形的各边中点得小正方形，将小正方形每边三等份，再将三等分点与大正方形的中心和一个顶点相连，那么图中阴影部分的面积总和等于________平方厘米。
4.由1、2、3、4四个数字组成的四位数共有24个，将它们从小到大排列起来，第18个数等于________。
5.已知两数的和被5除余1，它们的积是2924，它们的差是________。
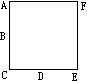
6．如右图，正方形ACEF 的边界上共有6个点A、B、C、D、E、F,其中B、D分别在边AC、CE上。那么，以这6个点中的三个点为顶点组成的不同的三角形的个数是________。
7.在从1到1998的自然数中，能被37整除，但不能被2整除，也不能被3整除的数的个数等于________。
8.小赵的电话号码是一个五位数，它由五位不同的数字组成。小张说：“它是84261。”小王说：“它是26048。”小李说：“它是49280。”小赵说：“谁说的某一位上的数字与我的电话号码上的同一位数字相同，就算谁猜对了这个数字。现在你们每人都猜对了位置不相邻的两个数字。”这个电话号码是________。
9.某商品每件成本72元，原来按定价出售，每天可售100件，每天利润为成本25％，后来按定价的90％出售，每天销售提高到原来的2.5倍，照这样计算，每天的利润比原来增加________元。
10.甲乙两列火车的速度比是5:4。乙车先发，从B站开往A站，当走到离B站72千米的地方时，甲车从A站发车往B站，两列火车相遇的地方离A、B两站的距离的比是3:4，那么A、B两站之间的距离为________千米。
11.大小猴子共35只，它们一起去采摘水蜜桃。猴王不在的时候，一只大猴子一小时可采15千克，一只小猴子一小时可采摘11千克。猴王在场监督的时候，每只猴子不论大小每小时都可多采摘12千克。有一天，采摘了8小时，其中只有第一小时和最后一小时有猴王在场监督，结果共采摘了4400千克水蜜桃。在这个猴群中，共有小猴子____只。
12.某次数学竞赛设一、二等奖。已知：
(1).甲、乙两校获奖人数的比为6:5；
(2).甲、乙两校获二等奖的人数总和占两校获奖人数总和的60％；
(3).甲、乙两校获二等奖的人数之比为5:6。
甲校获二等奖的人数占该校获奖总人数的百分数等于________。