小学奥数二年级:考察问题的全面和方法性,技巧以及结合图形研究问题。
| 速算与巧算 |
1,“凑整法”,把可以凑成整数的数放在一起计算,如果没有可以直接凑成整数的,想办法找出来。
24+44+56 52+69 45-18+19 45—18—19
2,相邻的两个数的差都相等的一串数就叫做等差连续数,又叫等差数列。
奇数个的方法:和=中间数*个数
偶数个的方法:和=(首数+末数)*个数的一半
1+2+3+4+5+6+7+…………………..+101
2+4+6+8+10+12+14+16+18+20
3,基准数法:在所有的数字中找到以某一个为基准,其他的数字向它靠拢。
23+20+19+22+18+21
102+100+99+101+98
计算下面的题:
87+74+85+83+75+77+80+78+81+84
9+18+27+36+45+54
| 数数和计数 |
数学需要观察,就是利用自己的想象能力,找出其中变化的规律。
1, 想想看,下面的黑白方块个有多少?
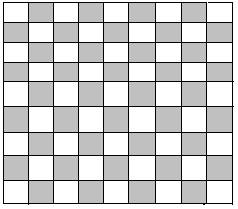
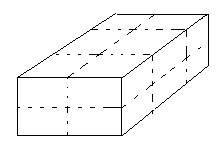
2如图,一个大长方体的表面上都涂上了红色,然后切成了18个小方块(如虚线所示)。在这些切成的小立方体中,问:
(1) 1面涂成红色的有几个?
(2) 2面涂成红色的有几个?
(3) 3面涂成红色的有几个?
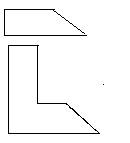
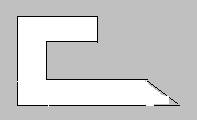
2, 墙上有一个漏洞,如图,用1号和2号两种特型砖块能补好吗?如果可以,需要几块?
| 数列问题 |
我们把按规律排列起来的一列数叫数列。学习数列关键就是通过分析数与数之间的关系,找出它们的规律,然后可以自己推导出其他的数。
如:常见的自然数列,奇数列,偶数列,等差数列,等比数列。
自然数列的规律就是后一个数比前一个数大一,自然增长。
奇数列的规律就是所有的数全部是奇数,而且后一个数比前一个数大2。
等差数列就是后一个数与前一个数的差值是一个固定的数。
![]()
![]() 等比数列就是后一个数与前一个数的商值是一个固定的数。
等比数列就是后一个数与前一个数的商值是一个固定的数。
1 如5,10,15,20, ,35,40,45
2 找规律:1,2,4,8,16, ,128,256
3找规律填空:1,2,4,7,11, ,29,37
4,一辆公共汽车有78个座位,空车出发,第一站上1为乘客,第二站上2为乘客,第三站上3为,依次下去,多少站以后,车上坐满乘客?(在坐满以前没有人下车)(数列求和?)
5,爸爸给小明100块糖,又给他10个盒子,要求小明往第一个盒子里放2块糖,第二个盒子里放4块糖,第三个盒子里放8块糖,第四个……….照这样下去,要放满这10个盒子,你说这100块糖够不够?
| 自然数列是关于自然数计数的问题,一般用到的方法是枚举法(即把你知道的所有情况都写出来) |
6,有一本书共200页,页码依次为1,2,3,……,199,200,问数字“1”在页码中共出现了多少次?(所有的情况都写出来,例如,分类讨论1在个位上的时候,1在十位上的时候,1在百位上的时候)
7,在1至100的奇数中,数字“3”出现了多少次?
8,像11,12,13这三个数,它们的数位上的各个数字相加之和是(1+1)+(1+2)+(1+3)=9。问自然数列的前20个数的数字之和是多少?
| 观察图形,找出规律,填涂接下去的部分 |
9观察下面的点组成的图形,请回答:


10 猜一猜,第3组的空白处应该填什么图?
![]()
![]()
![]()
11.按照下面的图形发展趋势,第四个图中应该如何填涂?第十个又是什么样子的呢?

1 2 3 4 5
学会从一般中找出规律,从而可以计算出任意的选项。通常可以写出1到4或者5,看出结果和这些数字的关系,是否有数列的关系,发现后可以写出通式。
1我们知道,如果一段线段上,加一个点,可以得到三个线段:![]()
如果一段线段上,加2个点,可以得到6个线段:
如果一段线段上,加3个点,可以得到多少个线段呢?加10个点呢?
2 两条直线相交,最多有1个交点,3条直线相交,最多三个交点,5条呢?10条呢?

(方法:一一列举出来,从前几个数字中找到规律,写出普通的规律式)
3 如图:一张大饼,切一刀最多切成2块,切2刀最多切成4块,切3刀最多切成7块,…….问切10刀最多可以切成多少块?

| 填图与拆数 |
填图是一种运算游戏,它要求把一些数字按照一定的规则填进各类图形,这不仅可以提高运算能力,而且更能让你去积极的思考问题,分析问题。
1 把1,2,3三个数字填到方格中,使的每行每列和每条对角线的三个数字的和都相等。
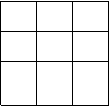 |
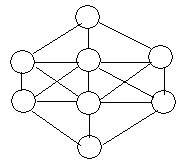
2 如图:由8个小圆圈组成,每个小圆圈都有直线和相邻的小圆圈相连接。请你把1,2,3,4,5,6,7,8八个数字分别填在八个小圆圈内,但相邻的两个数不能填入有直线相连的两个小圆圈。
3 三个圆圈两两相交形成七个小区域,分别填上1---7七个自然数,在一些小区域中,自然数3,5,7三个数已经填好,请你把其余的数填到空着的小区域中,要求每个圆圈中的四个数的和都是15。(先看看15可以用怎样的组合而成,由几个数字相加连接)

| 分情况讨论,考虑问题的全面性 |
有些数学问题,要求把符合条件的算式或得数全部找出来;若漏掉一个,答案就不对,所以做这种题的关键在强调有秩序的思考问题。
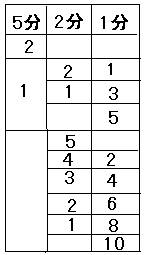
1 从2个5分硬币,5个2分硬币,10个1分硬币中,拿出1角钱来,有多少种不同的拿法?
(为了不至于遗漏,最好按照情况有秩序的分类,如:5分出现的可能是:2,1,0)
2 邮局门口有5级台阶,若规定一不只能上一级或者二级,问上这个台阶共有多少种不同的方法?
3 一个外国小朋友手里有4张3分的邮票和3张5分的邮票。请你帮他算一下可以组成多少中不同的邮资?
注:关键是学会用这样的方法,按秩序讨论,不错过任何一种情况。
4 一些十位数字和个位数字相同的二位数可以由十位数字和个位数字不同的两个二位数相加得到 ,如12+21=33。问在100之内有多少这样的组合?
注:有些还存在多组组合,要注意全面性
| 趣位问题:除了题干,要考虑其他的因素 |
1①树上有5只小鸟,飞起了一只,还剩几只?②树上有5只小鸟,“趴”的一声,猎人用枪打下一只,问树上还剩几只?
2 两个父亲和两个儿子一起上山打猎,每人都捉到一只野兔,拿回去数一数,共三只。为什么?
3 一个小岛上住着说谎的和说真话的两种人,说谎话的人句句说谎,说真话的人句句是实话。假想某一天你去小岛探险,碰到了岛上的三个人A,B,C,相互交谈中,有这样一段对话:
A说:B和C两人都说谎
B说:我没有说谎
C说:B确实在说谎。
请问,三人中,有几人在说谎,几个人说真话?
4 用三个火柴棍可以组成一个等边三角形。再给你三根,请组成四个等边三角形?(立体)
5 你能一笔把下面的九个点连接起来吗?(一次从头到尾,没有停顿。)

6 一家冷饮店规定,喝完汽水后,用4个空汽水瓶可以换1瓶汽水。老师带着32个学生进店后,他只买了24瓶汽水,问每个学生都能喝到汽水吗?
7 一个长方形,剪掉一个角后,剩余的部分还有几个角?
| 猜测题:在不断猜测中调整自己的思维 |
1 100个和尚分100个馒头,刚好分完。已知大和尚1个人3个馒头,小和尚3个人1个馒头,请问大小和尚各多少人?(从33开始摸索到25)
2 林林心里想到三个数,它们的和是12,又知第二个数比第一个大1,第三个比第二个大1,请猜出林林心里的这三个数分别是几?
3 有人问小虎今年几岁,他编了一道有趣的数学题回答说:“爷爷,爸爸和我,三个人的年龄和是120岁,爷爷比爸爸大30岁,爷爷和爸爸的年龄和刚好比我大100岁,你猜我今年几岁?”请问:你知道他们三个人分别是多少岁?
4 游泳池里男孩戴蓝帽,女孩戴红帽,一个男孩说:“我看见的蓝帽与红帽一样多”;一个女孩说:“我看见的蓝帽比红帽多一倍。”你知道游泳池中有几个男孩,几个女孩?
对于比较复杂的问题,可以用列表的方法,逐一的尝试:
5 老大,老二,老三兄弟三人岁数的和是32岁,老大比老二的岁数大3岁,而老大的岁数是老三的2倍,问兄弟三人个几岁?
(如果老三5岁,那么老大多少?…………)
6 原题:某学校的学生去郊游,中午开饭时,两个学生合用一个饭碗,三个学生合用一个菜碗,四个学生合用一个汤碗,共用了65只碗,问共有多少个学生?
7 兄弟两人去钓鱼,共钓了52条,其中弟弟钓的是哥哥的2倍多一条,问两人各跳了几条?
8 (古代传统问题)一只鸡有一个头2只脚,一只兔有一个头4只脚。如果一个笼子里关着的鸡和兔共有10个头和26只脚,你知道有几只鸡和几只兔吗?
9 把99粒棋子放在两种型号的17个盒子里,每个大盒子里放12粒,每个小盒子里放5粒,恰好放完。问大小盒子各多少个?
| 数学需要严谨,但也需要机智和顿悟。 |
1 有一个老妈妈,她有三个男孩,每个男孩又都有一个妹妹,问全家共有几口人?
2 公共汽车里,售票员对车内的人数数了一遍,便说道:车里没买票的人数是买票的人数的2倍。你知道车上买了票的乘客最少有几人?(隐含条件)
3 中午放学的时候,还在下雨,大家都盼望着晴天,小明对小英说:“已经连续三天下雨了,你说再过36小时会出太阳吗?”你认为会吗?
4 有人去买葱,他问多少钱了一斤,卖葱的人说:“1角钱1斤。”买葱的说:“我要都买了,不过要切开称。从中间切断,葱叶那段每斤2分,葱白那部分每斤8分。你卖不卖?”卖葱的一想:“8分+2分就是1角。”他就同意了,但是卖后一算帐,发现赔了不少钱。你知道为什么吗?
5 小明家附近有一个公园,园中有4棵树排成了一行。如图:想一想能不能把公园分为4块大小形状相同,而且每块上都有一棵树?
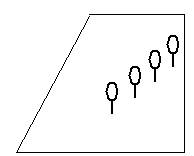
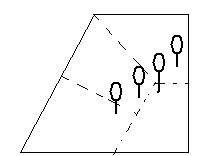
(一分四的梯形特性)
6 满满一杯牛奶,小明先喝了半杯;然后添水加满,之后再喝去半杯;再添一次水加满,最后把它全部喝完。请问小明一共喝了多少杯牛奶,多少杯水?
| 数与形题:形数与体数的引出 |
1 古希腊数学家毕达哥拉斯发现了“形数的奥秘比如他把1,3,6,10,15,…..叫做三角形数。因为用圆点按这些数可以堆垒成三角形,见下图:

从圆点的堆垒规律,发现每一个三角形数,都可以写成从1开始的n个自然数之和,最大 自然数就是三角形底边圆点的个数。
第一个数:1=1
第二个数:3=1+2
第三个数:6=1+2+3
第四个数:10=1+2+3+4
第五个数:15=1+2+3+4+5
……………………………….
第n个数:1+2+3+4+5+………..+n
可见,第n个三角形数=n(n+1)/2
根据这个公式可以写出任意一个指定的三角形数。
如:第100个三角形数是:100*(100+1)/2=5050
2 毕达哥拉斯还发现了四角形数,见下图:因为用圆点按四角形数可以堆垒成正方形,因此它们最受科学家的推崇。

第一个数:1=1
第二个数:4=2平方=1+3
第三个数:9=3平方=1+3+5
第四个数:16=4平方=1+3+5+7
第五个数:25=5平方=1+3+5+7+9
……………………………….
第n个数:n平方=1+3+5+7+9+………..+(2n-1)
四角形数可以表示成自然数的平方,也可以表示成从1开始的几个连续的奇数的和。奇数的个数就等与正方形的一条边上的点数。
类似的还有四面体数,五面体数等,你能归纳出四面体数的规律吗?
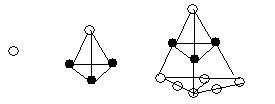
1
4=1+3
10=1+3+6
….????
| 看图找规律: |
关键在学会找出给出的数字和图形之间的关系
1 在空白的地方填写合适的数
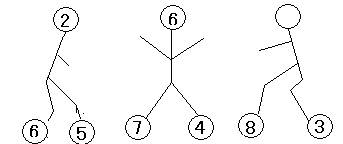
分析它们之间到底有什么规律存在?
2在空格的地方填写合适的数

3 在空格的地方填写合适的数
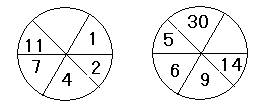
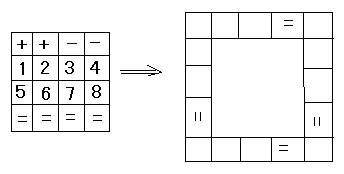
4 根据所给出的数字和符号排出算式:
| 拆数字游戏: |
把15个小球分成数量不同的4堆,共有多少种不同的分法?(美国奥数题)
美国硬币有1分,5分,10分和25分四种。现有10枚硬币价值是1元,其中有3枚25分的硬币。问余下的有哪几种,每种各多少枚?(美国奥数原题)
小虎给3个小朋友写信,由于粗心,把信装入信封时都给装错了,结果3个小朋友收到的都不是给自己的信,请问小虎错装的情况有多少种可能?(即写出谁受到应该给谁的信,可以列表表示清楚)
假若20只兔子可以换2只羊,9只羊可以换3头猪,8头住可以换2头牛,那么5头牛可以换多少只兔子?