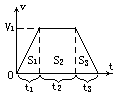
第一章 牛顿运动定律
一、 选择题：
1、下列关于惯性的说法，正确的是（ ）
（A）只有静止或做匀速直线运动的物体才具有惯性
（B）做变速运动的物体没有惯性
（C）有的物体没有惯性
（D）两个物体质量相等，那么它们的惯性大小相等
2、图甲为具有水平轴的圆柱体，在其A点放一质量为M的小物块P，圆柱体绕其有自身轴O缓慢地匀速转动.设从A转至A′的过程中，物块与圆柱体保持静止，则表示物块受摩擦力f大小随时间变化的图线是图乙中 ( )
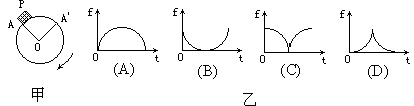
3、关于作用力和反作用力，下列说法正确的是（ ）
（A）作用力和反作用力作用在不同物体上
（B）地球对重物的作用力大于重物对地球的作用力
（C）作用力和反作用力的大小有时相等，有时不相等
（D）作用力和反作用同时产生，同时消失
4、一个铅球和一个皮球相互挤压的时候，以下叙述正确的是（ ）
（A）铅球对皮球的压力大于皮球对铅球的压力
（B）铅球的形变小于皮球的形变
（C）皮球对铅球的压力和铅球对皮球的压力一定同时产生
（D）铅球对皮球的压力与皮球对铅球的压力是一对平衡力
5、一个静止的质量为m的不稳定原子核，当它完成一次a 衰变，以速度v发射出一个质量为ma 的a 粒子后，其剩余部分的速度等于：
(A)－
； (B)－v；
(C)
； (D)
。
6、一个置于水平地面上的物体受到的重力为G, 当用竖直向下的恒力F压它时, 则物体对地面压力大小是( )
(A) F (B) G (C) G+F (D) G－F
7、重500N的物体，放在水平地面上，物体与地面间的滑动摩擦因数为0.30，用多大的水平力推物体，才能使物体维持匀速直线运动状态不变（ ）
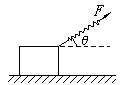
（A）100N （B）150N （C）200N （D）500N
8、两个具有相等动量的物体，质量分别为m1和m2，且m1 >m2，比较它们的动能，则：
(A)m2的动能较大； (B)m1的动能较大；
(C)动能相等； (D)不能确定。 ( )
9、一人从泊在码头边的船上往岸上跳，若该船的缆绳并没拴在码头上，下列说法中正确的有：
(A)船越轻小，人越难跳上岸；
(B)人跳时对船速度大于对地速度；
(C)船越重越大，人越难跳上岸；
(D)人跳时对船速度等于对地速度。 ( )
10、要计算竖直上抛一个物体时手对抛出物作用力的冲量，如不计空气阻力，所需的已知条件为下列几种组合中的：( )
(A)物体的质量m，它能上升的最大高度H；
(B)抛出时的初速v0，它能上升的最大高度H；
(C)抛出时用力F的大小，物体上升到最高处所需的时间t；
(D)物体的重量G，它在空中的时间
。
二、 填空题：
11、物体放在桌上处于静止，它所受的重力的反作用力作用在_____上；重力的平衡力是____；桌面支持力的反作用力是____。
12、一辆小车在光滑的水平面上，若用一水平力F1拉它，它的速度在0．5s内从0．4m/s增大到0．8m/s；若用水平力F2拉它，它的速度在0．3s内从0．5m/s减小到0．2m/s，那么F1和F2的大小之比是_____。
13、质量为m的物体，在两个大小相等、夹角为120°的共点力作用下，产生的加速度大小为a，当两个力的大小不变，夹角变为0°时，物体的加速度大小变为____；夹角变为90°时，物体的加速度大小变为_____。
14、一个物体放在光滑的水平面上，处于静止。从某一时刻t=0起，受到如下图所示的力F的作用，设力F的正方向为向北，物体的质量为m＝10kg。物体在5s末的位移是____；速度是____，方向_____，物体在10s末的位移是____；速度是_____，方向_____
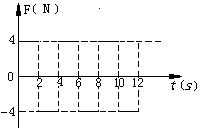
15、用恒力F在时间t内能使质量为m的物体，由静止开始移动一段距离s，若用F/2恒力，在时间2t内作用于该物体，由静止开始移动的距离是_____。
16、某同学做验证牛顿第二定律的实验，使用的器材有：带滑轮的长木板、小车及往小车摆放的大砝码、细线、小桶及往小桶里放的小砝码、打点计时器等。
（1）他以小桶及小桶内的砝码的总重力作为细线对小车的拉力F，测出不同拉力F对应的加速度a值，并把各数据标在a-F坐标系上，发现它们都在一条直线的附近，这条直线不过坐标原点，如图（甲）所示，而与横坐标轴交于F1点，产生这种情况的原因是什么？
答：________________________________________________________________
（2）经过调整后，该同学作出的a-F图像如图（乙）中的A所示，另一位同学使用同一套仪器作出的a-F图像如图（乙）中的B所示。B图像的斜率比A图像的斜率小的原因是什么？
答：________________________________________________________________
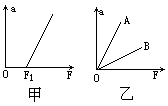
17、在粗糙的水平面上用水平恒力F推动质量为m的物体，由静止开始运动，经过了3 s撤去外力后，又经过2 s物体停止运动，则物体与水平面的滑动摩擦系数为________。
18、物体在力F1作用下获得正西方向4 m/s2的加速度，在力F1和力F2共同作用下获得正北方向3 m/s2的加速度。那么物体在力F2单独作用下的加速度大小是_____ 。
19、甲、乙两个物体的质量之比为2：1，受到的合外力的大小之比是1：2，甲、乙两个物体都从静止开始运动，那么，两个物体经过相同的时间通过的路程之比为_____。
20、两个小球的质量分别为m1和m2，且m1 =2m2，当它们的动能相等时，它们的动量之比p1∶p2 =__________。
三、 计算题：
21、水平方向恒力F将一个质量为5kg的木块压在竖直墙壁上,如图,木块与墙壁之间的摩擦系数
=0.2,要使木块沿竖直方向匀速下滑,那么作用力F的值是多少?
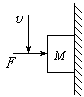
22、质量为3kg的木箱静止在水平地面上,在水平恒力F的作用下运动,4s末它的速度达到4m/s.此时将力F撤去,又经过6s物体停止运动,若地面与木箱之间的动摩擦因数不变,求力F的大小.
23、用细绳拉着物体向上做匀加速运动,当拉力F=140N时,物体向上的加速度是4m/s2,g取10m/s2,求：
(1)物体的质量多大?
(2)物体从静止开始在前2s的位移及2s末的速度各多大?
24、静止在水平地面上的物体,质量为20kg,现在用一个大小为60N的水平推力使物体做匀加速直线运动,当物体移动9.0m时,速度达到6.0m/s,求：
(1)物体加速度的大小.
(2)物体和地面间的滑动摩擦系数.(g取9.8m/s2)
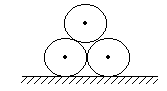
25、在地面上放置两个相互紧靠在一起的圆柱形木柱，在它们上面放置同样的圆木,如图，问圆木之间的摩擦系数μ至少多大时，它们才会滚散?设圆木与地面的摩擦力足够大.
26、如图所示，在光滑水平面上停有一辆质量为M的小车，车身长为
，一个质量为m的质点放在车的尾部。A与车之间的摩擦系数为m ，现给质点A以水平速度v0向右运动，设A与小车的前后档板碰撞中动能不损失。求：
(a)质点A和小车相对静止时，小车速度是多大？
(b)质点A相对小车静止前与小车前后档板碰撞的总次数是多少？(提示：每碰一次相对步车滑行，碰n次，则相对车滑行n
)
27、一个质量m=10kg的物体放在水平地面上,物体与地面间的摩擦系数μ=0.4,轻弹簧的一端系在物体上,如图.当用力F与水平方向成θ=37o角拉弹簧时,弹簧的长度由10cm伸长到13cm，物体沿水平面做匀速直线运动.g取10m/s2,求弹簧的劲度系数.
28、一根轻质弹簧, 倔强系数为K. 当弹簧竖直吊起质量为10kg的物体, 物体处于静止状态, 弹簧伸长了10.0cm; 用弹簧拉着该物体沿粗糙水平面滑动, 当弹簧沿与水平方向成370斜向上拉时, 弹簧伸长4.0cm, 物体恰沿水平面做匀速直线运动; 当弹簧沿水平方向拉物体, 弹簧伸长5.0cm时, 物体做匀加速直线运动.(g取10m/s2, sin370=0.6, cos370=0.8) 求：
(1) 弹簧的倔强系数K.
(2) 物体与水平面间的滑动摩擦系数μ.
(3) 物体做匀加速直线运动的加速度a.
29、一平直的传送带以速率v=2m/s匀速运行，传送带把A处的工件运送到B处，A、B相距L=10 m。从A处把工件轻轻放到传送带上，经过时间t=6s能传送到B处。如果提高传送带的运行速率，工件能较快地从A处传送到B处。要让工件用最短时间从A处传送到B处，说明并计算传送带的运行速率至至少应多大？
30、质量为1kg, 初速度为10m/s的物体, 沿粗糙水平面滑行, 如图所示, 物体与地面间的滑动摩擦系数为0.2, 同时还受到一个与运动方向相反的, 大小为3N的外力F作用, 经3s钟后撤去外力, 求物体滑行的总位移. (g取10/s2)
答 案
一、 选择题： 1、D 2、D 3、AD 4、BC 5、D 6、C 7、B 8、A 9、AB 10、A
二、 填空题：
11、地球；支持力；物体对桌面的压力
12、2：5
13、2a；
a
14、1.8m；0．4m/s；向北；4 m；0．8 m/s；向北
15、2s
16、(1)未平衡摩擦力或平衡摩擦力不够
(2)B图像表示小车及车上砝码总质量较大
17、3F/5mg
18、5m/s2
19、1：4
20、
∶1
三、 计算题：
21、木块匀速下滑f=G=49N
f=N=F ∴F=f/=245N
22、vt=a1t1,a1=1m/s2,vt=a2t2=
m/s2,f=ma2=3×
=2N
F-f=ma1,F=f+ma1=5N
23、解：(1)F-mg=ma,F=m(g+a)
m=
=10kg
(2)s=
at2=8m
v=at=8m/s
24、(1)vt2=2as,a=
=2m/s2
(2)F-f=ma,f=mg,mg=F-ma
=
≥0.1
25、μ=0.27
26、(a)mv0 /(M＋m) (b)Mv02/2m g(M＋m)
27、Fcos
=(G-Fsin)
F(cos+sin)=u)=G (1)
F=k
x (2)
解出：k=1282N/m
28、(1) ∵F=kx
∴
(2) 分析图略
F′=kx=10×4.0N=40N
(3)
29、解：工件放到A端受传送带恒定的滑动摩擦力作用做匀加速运动，速度由0增大到v；再随传送带一起匀速运动到B外。
工件加速运动时间为t1，位移
工件加速运动时间为t2，位移s2=vt2
其中v=at1，t1＋t2=t，s1＋s2=L
解得 a=1 m/s2
提高传送带速率为v′(v′＞v)时，工件加速运动所受滑动摩擦力不变、a不变、加速时间延长，由A到B的时间缩短，工件由A到B一直处于加速运动时所用时间最短。
设最短时间为t′，则
，
所以 
工件到B时速度
即传送带速率至少应等于4.47m/s。
30、在外力F作用下, 物体先做匀减速运动, a1=(F+f)/m=(3+0.2×1×10)/1=5m/s2, 经过t1=v0/a=10/5=2s, 物体速度减为零; 接下来, 物体将向左匀加速运动1s, a2=(F－f)/m=(3－0.2×1×10)/1=1m/s2; 之后, 撤掉外力F, 物体在f作用下, 向左匀减速运动直至停止, a3=μg=0.2×10=2m/s2; 物体向右位移S1=v0t1/2=10×2/2=10m, 物体向左位移S2=a2t22/2=1×12/2=0.5m; S3=v22/(2a3)=(a2t2)2/(2a3)=(1×1)2/(2×2)=0.25m;
总位移为S=S1－(S1+S2)=10－(0.5+0.25)=9.25m, 位于出发点右侧.
