平抛物体的运动（习题课）
一、教学目标
1、熟练掌握平抛运动的规律，学会用平抛运动的规律解决实际问题的方法。
2、理解平抛运动可以看作水平方向的匀速直线运动与竖直方向的自由落体运动的合运动，并且这两个运动互不影响。
二、重点、难点
重点：平抛运动的特点和规律。
难点：对平抛运动的两个分运动的理解和运用。
三、教学方法：
讲练结合
四、教学用具：
幻灯片、投影仪
五、教学过程
（一）导入新课：
上节课我们学习了平抛运动的知识，这节课我们通过习题课加深对上节课知识的理解，并学会利用平抛运动的知识解决实际问题的方法。
（二）知识复习（教师提问，学生回答）
1、什么是平抛物体的运动？
答：将物体用一定的初速度沿水平方向抛出，不考虑空气阻力，物体只在重力作用下所做的运动，叫做平抛运动。
2、平抛运动可以分解为哪两个分运动？这两个分运动有何关系？
答：做平抛运动的物体，在水平方向上由于不受力，将做匀速直线运动；在竖直方向上物体的初速度为0，且只受到重力作用，物体做自由落体运动，加速度等于g。这两个分运动是独立的，互不干涉，独立进行，且时间相等。
3、写出平抛运动的规律。
1．平抛运动的物体在任一时刻t的位置坐标
a：以抛出点为坐标原点，水平方向为x轴（正方向和初速度v0的方向相同），竖直方向为y轴，正方向向下，则物体在任意时刻t的位置坐标为
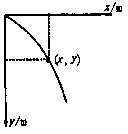
b：运用该公式我们可以求得物体在任意时刻的坐标并找到物体所在的位置，然后用平滑曲线把这些点连起来，就得到平抛运动的轨迹，这个轨迹是一条抛物线。
2、平抛运动的速度
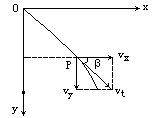a：水平分速度
b：竖直分速度
c：t秒末的合速度
d：
的方向
（三）例题精讲
【例1】（投影）
宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L．若抛出时的初速度增大到2倍，测得抛出点与落地点之间的距离为
。已知两落地点在同一水平面上，求该星球的重力加速度g．
分析与解：
这是一道对平抛运动规律实际应用的题．应该注意两点：
（1）“抛出点与落地点之间的距离”不是“水平射程”；
（2）“重力加速度”不是地面上的g=9.8m/s2。
由于抛出点的高度不变，所以两次运动的时间相同，竖直位移均等于
，水平位移分别为x1=x和x2=2x，由平抛运动的位移公式得
L2=x2+y2
解得 
由
得 
【例2】（投影）
如图所示，物体做平抛运动的轨迹，在任一点P（x,y）的速度方向的反向延长线交于x轴上的点A，则OA的长为多少？
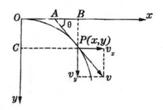分析与解：
本题要求OA的长，OA=x-AB
而
AB=ycotθ，,cotθ=
，
所以 AB=ycotθ=
=
所以
OA=
（四）课堂练习
1．做平抛运动的物体，每秒的速度增量总是 [ ]
A．大小相等，方向相同
B．大小不等，方向不同
C．大小相等，方向不同
D．大小不等，方向相同
2．从倾角为θ的足够长的斜面上的A点，先后将同一小球以不同的初速度水平向右抛出．第一次初速度为v1，球落到斜面上的瞬时速度方向与斜面夹角为α1，第二次初速度为v2，球落到斜面上的瞬时速度方向与斜面夹角为α2，若v1＞v2，则 [ ]
A．α1＞α2
B．α1=α2
C．α1＜α2
D．无法确定
3．如图所示，斜面倾角为θ，小球从斜面上的A点以初速度v0水平抛出，恰好落到斜面上的B点．求：（1）AB间的距离；（2）小球从A到B运动的时间；（3）小球何时离开斜面的距离最大？
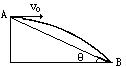
参考答案
1．A 2．B
3．（1）
（2）
（3）
六、说明
1．平抛运动是学生接触到的第一个曲线运动，弄清其成因是基础，水平初速度的获得是问题的关键，可归纳为两种：
(1)物体被水平加速：水平抛出、水平射出、水平冲击等；
(2)物体与原来水平运动的载体脱离，由于惯性而保持原来的水平速度。
2．平抛运动的位移公式和速度公式中有三个含有时间t，应根据不同的已知条件来求时间。但应明确：平抛运动的时间完全由抛出点到落地点的竖直高度确定(在不高的范围内g恒定)，与抛出的速度无关。