高一物理试卷
《曲线运动 万有引力定律》测试卷
班级 姓名 学号 得分
一、选择题（下列各题四个选项中有一个或几个符合题意）（每小题4分，共40分）
1.从距地面高h处水平抛出一小石子,空气阻力不计,下列说法正确的 （ ）
A.石子运动速度与时间成正比
B.石子抛出时速度越大,石子在空中飞行时间越长
C.抛出点高度越大,石子在空中飞行距离越长
D.石子在空中任何时刻的速度与其竖直方向分速度之差为一恒量
2. 关于物体的平抛运动,下列说法正确的是:（ ）
A 由于物体受力的大小和方向不变, 因此平抛运动是匀变速运动;
B 由于物体速度的方向不断变化, 因此平抛运动不是匀变速运动;
C 物体的运动时间只由抛出时的初速度决定,与高度无关;
D 平抛运动的水平距离由抛出点的高度和初速度共同决定.
3．如图所示，在不计滑轮摩擦和绳子质量的条件下，当小车匀速向右运动时，物体A的受力情况是( )
A．绳的拉力大于A的重力 B．绳的拉力等于A的重力
C．绳的拉力小于A的重力 D．拉力先大于重力，后变为小于重力
4．1999年5月10日，我国成功地发射了“一箭双星”，将“风云1号”气象卫星和“实验5号”科学试验卫星送入离地面870km的轨道，已知地球半径为6400km，这两颗卫星的速度约为（ ）
A．11.2km/s B．7.9km/s C．7.4km/s D．1km/s
5．人造地球卫星进入轨道做匀速圆周运动时（ ）
A．卫星的运动周期与地球质量无关
B．卫星上的物体不再受到重力的作用
C．卫星在轨道上运行的线速度应大于第一宇宙速度
D．同步卫星都在同一条轨道上运行，轨道在地球赤道平面内
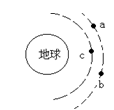
6．如图，a、b、c是环绕地球的圆形轨道上运行的三颗人造地球卫星，a、c的质量相同且小于b的质量，则（ ）
A．a、b的线速度大小相等，且小于c的线速度
B．a、b的周期相同，且大于c的周期
C．a、b的向心加速度大小相等，且大于c的向心加速度
D．a所需的向心力最小
7．如某星球的密度与地球相同，又知其表面处的重力加速度为地球表面重力加速度的2倍，则该星球的质量是地球质量的（ ）
A．8倍 B．4倍 C．2倍 D．1倍
8．已知某星球半径为r，沿星球表面运行的卫星周期为T，据此可求得（ ）
A．该星球的质量 B．该星球表面的重力加速度
C．该星球的自转周期 D．该星球同步卫星的轨道半径
9．如图所示，A、B、C三物体放在旋转圆台上，与台面的动摩擦因数为μ，A的质量为2m，B与C的质量均为m，A、B离轴距离均为a，C离轴为2a，当圆台旋转时，A、B、C都没有滑动，则（ ）
A．C物体受到的向心力比A物体受到的向心力大 B．B物体受到的静摩擦力最小
C．圆台角速度增加时，B比C先滑动 D．圆台角速度增加时，B比A先滑动
10．在光滑的圆锥漏斗的内壁，有两个质量相等的小球A、B，它们分别紧贴漏斗，在不同水平面上做匀速圆周运动，如图6所示，则下列说法正确的是（ ）
A．小球A的速率大于小球B的速率
B．小球A的速率小于小球B的速率
C．小球A对漏斗壁的压力大于小球B对漏斗壁的压力
D．小球A的转动周期小于小球B 的转动周期
二、填空题（每题5分,共20分。）
11如图是某同学实验得到的小球做平抛运动的轨迹，建立了坐标系，测出了a、b、c三点的坐标，g取10m／s2，根据图中数据回答：小球做平抛运动的初速度是_________m／s．
12．在一次“飞车越黄河”的表演中，汽车在空中飞过最高点后在对岸着地。已知汽车从最高点至着地点经历时间约0.8s，两点间的水平距离约为30m，忽略空气阻力，则着地点与最高点间的高度差约为 m.(g取10m/s2)
13．已知地球表面重力加速度为g,地球半径为R,万有引力恒量为G,用以上各量表示,地球质量M= 。
14．地球的质量是月球的81倍，一飞行器在地球与月球之间，当地球对它的引力和月球对它的引力相等时，飞行器距地心的距离与距月心距离之比是________．
三、论述计算题（共90分）
15、(14分)A、B两小球同时从距地面高为h=15m处的同一点抛出，初速度大小均为v0=10m/s．A球竖直向下抛出，B球水平抛出，空气阻力不计，重力加速度取g=l0m／s2．求：
(1)A球经多长时间落地?
(2)A球落地时，A、B两球间的距离是多少?
16． (14分)有一小船正在渡河，如图11所示，在离对岸30 ｍ时，其下游40ｍ处有一危险水域.假若水流速度为5 m/s，为了使小船在危险水域之前到达对岸，那么，小船从现在起相对于静水的最小速度应是多大?
17、(15分)宇航员在某行星的极地上着陆，发现自己在当地的重力是在地球上重力的0.01倍，进一步研究还发现，该行星的一昼夜的时间与地球相同，而且物体在其赤道上随其行星自转时恰好完全失去重力，试计算这一行星的半径R（结果保留两位有效数字）。
18、(15分)如图所示, 在内壁光滑的平底试管内放一个质量为1g的小球, 试管的开口端加盖与水平轴O连接. 试管底与O相距5cm, 试管在转轴带动下沿竖直平面做匀速圆周运动. 求：(1) 转轴的角速度达到多大时, 试管底所受压力的最大值等于最小值的3倍.(2) 转轴的角速度满足什么条件时,会出现小球与试管底脱离接触的情况?
19、．(16分)如图所示，有一根长为2L的轻质细线，它的两端固定在一根长为L的竖 直转轴AB上，线上套一个可以自由移动的小环，当转轴转动时，小环正好以B为圆心，在水平面内做匀速圆周运动，求细线的张力和小球的线速度。
20、(16分)设想宇航员完成了对火星表面的科学考察任务，乘坐返回舱返回围绕火星做圆周运动的轨道舱，如图所示。为了安全，返回舱与轨道舱对接时，必须具有相同的速度。已知返回舱返回过程中需克服火星的引力做功
，返回舱与人的总质量为m，火星表面的重力加速度为g ，火星的半径为R，轨道舱到火星中心的距离为r，不计火星表面大气对返回舱的阻力和火星自转的影响，则该宇航员乘坐的返回舱至少需要获得多少能量才能返回轨道舱？
参考答案：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | AD | A | D | ABD | A | A | AB | B | A |
11.2m/s
12.3.2m
13.gR2/G
14.9:1
15.t=1s, 
16.3m/s
17.R=1.9×107 m
18.
19.
20.
，