匀速圆周运动(一)
知识要点:
知道什么是匀速圆周运动,理解圆周运动是变速运动。理解线速度的概念,知道线速度就是物体做匀速圆周运动的瞬时速度,理解角速度、周期、频率和转速的概念,会用有关公式进行计算。理解线速度、角速度、周期、频率和转速之间的关系,会用有关公式进行计算。
1. 匀速圆周运动、圆周运动;运动轨迹为圆或圆的一部分,这样的运动叫圆周运动。如果质点沿圆周运动,在相等的时间里通过的弧长相等,这种运动叫匀速圆周运动。
匀速圆周运动的轨迹为曲线,所以匀速圆周运动是变速运动,匀速是运动的快慢程度不改变。
匀速圆周运动是变速运动,所以做匀速圆周运动的物体状态是非平衡态,所受合外力不为零。
2. 描述圆周运动的物理量
(1)线速度:线速度大小又叫速率,用![]() 表示,
表示,![]() ,S为弧长,
,S为弧长,![]() 为通过这段弧长的时间,速率越大则沿弧运动得越快。
为通过这段弧长的时间,速率越大则沿弧运动得越快。
线速度的方向为圆的切线方向。
线速度就是圆周运动的瞬时速度。
(2)角速度:连接质点和圆心的半径转过的角度![]() ,与所用时间比叫角速度
,与所用时间比叫角速度![]() 。
。
![]() 的单位是弧度,时间
的单位是弧度,时间![]() 单位是秒,
单位是秒,![]() 的单位就是弧度/秒,用字母表示为
的单位就是弧度/秒,用字母表示为![]() 角速度的大小描述了做圆周运动绕圆心转动快慢程度。角速度大则绕圆心转得快。对一个不变形的物体转动中任何点转过的角度都相同,所以角速度都相同。
角速度的大小描述了做圆周运动绕圆心转动快慢程度。角速度大则绕圆心转得快。对一个不变形的物体转动中任何点转过的角度都相同,所以角速度都相同。
(3)周期:使圆运动运动一周的时间叫周期用字母T表示,单位为秒。
周期描述圆周运动重复的快慢,也反映了转动快慢。周期越小,转动越快。
(4)频率:1秒内完成圆周运动的次数叫频率。它是周期的倒数,单位是1/秒。用符号![]() 表示单位又叫赫兹(
表示单位又叫赫兹(![]() ),
),![]() 越大,转动就越快。
越大,转动就越快。
(5)转速:工程技术中常用。定义为每秒转过的圈数,数值与频率相同,单位也是1/秒。
各量之间的关系,线速度与角速度![]() ,
,
![]()
![]() ,
,![]()
R一定,![]() 与
与![]() 成正比,
成正比,![]() 一定
一定![]() 与R成正比,
与R成正比,![]() 一定,
一定,![]() 与R成反比。
与R成反比。
(6)![]() 的关系:
的关系:
![]()
![]()
![]()
(7)向心加速度
① 物理意义:描述线速度方向改变的快慢。
②
大小:![]()
③ 方向:总是指向圆心,与线速度方向垂直
3. 匀速圆周运动
(1)定义:做圆周运动的物体,若在相等的时间里通过的圆弧长度相等,就是匀速圆周运动。
(2)运动学特征:线速度大小、向心加速度大小不变,但方向时刻改变,故匀速圆周运动是变速运动。
4. 向心力
(1)作用效果:产生向心加速度,以不断改变物体的速度方向,维持物体做圆周运动。
(2)大小:![]()
(3)产生:向心力是按效果命名的力,不是某种性质的力。
5. 向心加速度的分析
向心加速度是向心力的效果,其方向与向心力相同,总是指向圆心。
从运动的角度看,向心加速度是描述做匀速圆周运动的物体的速度方向变化情况的物理量,其计算公式![]()
![]()
由上式可以看出:当线速度v一定时,向心加速度a跟轨道半径r成反比;当角速度ω一定时,向心加速度a跟r成正比;由于![]() ,所以a总是跟v与
,所以a总是跟v与![]() 的乘积成正比。
的乘积成正比。
6. 圆周运动中向心力的特点
(1)匀速圆周运动:由于匀速圆周运动仅是速度方向变化而速度大小不变,故只存在向心加速度,物体受到外力的合力就是向心力。可见,合外力大小不变,方向始终与速度方向垂直且指向圆心,是物体做匀速圆周运动的条件。
(2)变速圆周运动:速度大小发生变化,向心加速度和向心力都会相应变化.求物体在某一点受到的向心力时,应使用该点的瞬时速度,在变速圆周运动中,合外力不仅大小随时间改变,其方向也不沿半径指向圆心,合外力沿半径方向的分力提供向心力,使物体产生向心加速度,改变速度的方向,合外力沿轨道切线方向的分力,使物体产生切向加速度,改变速度的大小。
【典型例题分析】
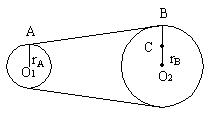
[例1] 皮带传动装置![]() ,
,![]() ,求
,求![]() 与v的大小关系?
与v的大小关系?
解析:A与B线速度大小相等,![]() ,两轮转动角速度不等,
,两轮转动角速度不等,![]()
![]()
A轮转得快,同一轮上的B与C角速度相等,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
[例2] 地球的半径约为R=6400km,试计算:
(1)赤道上的物体随地球自转的线速度多大?
(2)北纬![]() 的地方,随地球自转的角速度、线速度各是多少?
的地方,随地球自转的角速度、线速度各是多少?
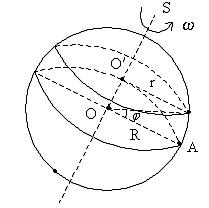
解析:地面上的物体随地球自转的角速度与地球的角速度相等,
![]() s
s
![]()
![]()
北纬![]() 的地方随地球自转圆心在地轴上,圆周运动半径为
的地方随地球自转圆心在地轴上,圆周运动半径为![]() ,
,![]()
![]()
![]()
![]()
![]()
[例3] 大型转盘,在水平面内绕竖直轴转动,在转动盘的边缘上的人向转盘中心的靶子瞄准射击,能否击中靶子?若不能,应该怎样瞄准才能击中靶子,设转盘半径为R,角速度为![]() 。
。
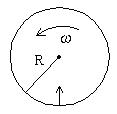
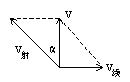
解析:立于中心处的靶子对地无移动。而人与发射出的子弹都有对地的线速度,子弹发射出后对地速度是线速度与发射速度的矢量合。设线速度为![]() ,发射速度为
,发射速度为![]() ,子弹速度为
,子弹速度为![]() ,
,![]() 的方向与发射时线速度方向夹角为
的方向与发射时线速度方向夹角为![]() ,
,
![]() ,
,![]()
![]() ,∴ 子弹不能击中靶子。
,∴ 子弹不能击中靶子。
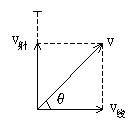
要想击中靶子,子弹的实际运动即合运动的速度方向指向靶子才行。
![]()
![]()
注意只有![]() 才能使上式成立。
才能使上式成立。
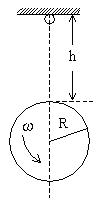
[例4] 如图所示,小球Q自空中自由下落从转动的圆形纸筒穿过。如图所示,纸筒绕水平轴匀速转动,已知转动角速度![]() ,半径
,半径![]() ,
,![]() 取
取![]() ,若小球穿筒壁时能量损失不计,撞击时间也可不计,小球穿过后纸筒上只留下一个孔。试求小球下落小高度
,若小球穿筒壁时能量损失不计,撞击时间也可不计,小球穿过后纸筒上只留下一个孔。试求小球下落小高度![]() 是多少?
是多少?
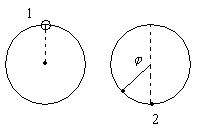
解析:小球穿过纸筒应有两次过筒壁,小球沿直径运动时间,等于第一次穿孔半径转过一定角度的时间![]() ,当小球速度足够大时,纸筒没转过一周上式中
,当小球速度足够大时,纸筒没转过一周上式中![]() ,若速度足够大就是下落高度足够大。设小球穿入纸筒的速度为
,若速度足够大就是下落高度足够大。设小球穿入纸筒的速度为![]() ,穿出的速度为
,穿出的速度为![]() 。
。
![]() ,纸筒只留一个孔,恰好转过半周
,纸筒只留一个孔,恰好转过半周![]()
而![]()
![]()
∴ ![]()
![]() 解得:
解得:![]()
【模拟试题】
1. 关于匀速圆周运动的角速度和线速度,下列说法正确的是( )
A. 半径一定,角速度与线速度成反比
B. 半径一定,角速度与线速度成正比
C. 线速度一定,角速度与半径成正比
D. 角速度一定,线速度与半径成反比
2. 质点做匀速圆周运动时,下列说法正确的是( )
A. 线速度越大,周期一定越小
B. 角速度越大,周期一定越小
C. 转速越大,周期一定越小
D. 圆周半径越小,周期一定越小
3. 机械表的时针与分针做圆周运动( )
A. 分针角速度是时针角速度的12倍
B. 分针角速度是时针速度的60倍
C. 如果分针的长度是时针长度的1.5倍,则分针端点的线速度是时针端点线速度的18倍
D. 如果分针的长度是时针长度的1.5倍,则分针端点的线速度是时针端点线速度的1.5倍
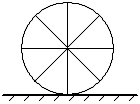
4. 如图所示,电视画面每![]() s更迭一帧,当屏幕上出现一辆车匀速奔驰的情景时,观众如果注视车轮的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布的完全相同的辐条,试问:下列说法哪些正确( )
s更迭一帧,当屏幕上出现一辆车匀速奔驰的情景时,观众如果注视车轮的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布的完全相同的辐条,试问:下列说法哪些正确( )
A. 若在![]() s内,每根辐条恰好转过45°,则观众觉得车轮是不动的
s内,每根辐条恰好转过45°,则观众觉得车轮是不动的
B. 若在![]() s内,每根辐条恰好转过365°,则观众觉得车轮是不动的
s内,每根辐条恰好转过365°,则观众觉得车轮是不动的
C. 若在![]() s内,每根辐条恰好转过365°,则观众觉得车轮是倒转的
s内,每根辐条恰好转过365°,则观众觉得车轮是倒转的
D. 若在![]() s内,每根辐条恰好转过355°,则观众觉得车轮是倒转的
s内,每根辐条恰好转过355°,则观众觉得车轮是倒转的
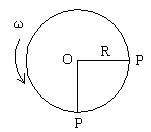
5. 如图所示,一圆盘绕过O点的竖直轴在水平面内旋转,角速度为ω,半径R,有人站在盘边缘P点处面对O随圆盘转动,他想用枪击中盘中心的目标O,子弹发射速度为V则( )
A. 枪应瞄准O点射击
B. 枪应向PO左偏过θ角射击,cos![]() =
=![]()
C. 枪应向PO左方偏过θ角射击,tan![]() =
=![]()
D. 枪应向PO左方偏过θ角射击,sin![]() =
= ![]()
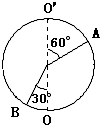
6. 如图所示为一球体绕轴OO’以角速度![]() 旋转,A、B为球体上的两点,下面几种说法正确的是( )
旋转,A、B为球体上的两点,下面几种说法正确的是( )
A. AB两点具有相同的角速度
B. AB两点具有相同的线速度
C. A、B两点加速度方向都指向球心
D. A、B两点的转动周期相同
7. 甲沿着半径为R的圆周跑道匀速跑步,乙沿着半径为2R的圆周跑道匀速跑步.在相同的时间内,甲、乙各自跑了一圈,他们的角速度和线速度分别为ω1、ω2和v1、v2,则( )
A. ![]() ,
,![]() B.
B.
![]() ,
,![]()
C. ![]() ,
,![]() D.
D.
![]() ,
,![]()
8. 地球自转的周期是 s;地球的半径为6400km,放在赤道上的物体随地球自转运动的线速度是 m/s。
9. 手表分针的长度为1.8cm,转轴到手表分针尖端的距离是1.5cm,则分针尖端的线速度的大小是 m/s。
10. 已知某人骑自行车1.0分钟蹬了10圈,车轮与脚蹬轮盘转数之比为3:1,车轮边缘转动的线速度大小为 m/s。(车轮直径为0.7m)
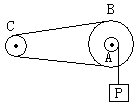
11. 如图所示,在轮B上固定有同轴小轮A,轮B通过皮带带动轮C,皮带和两轮之间没有滑动,A、B、C三轮的半径依次为r1、r2和r3,绕在A轮上的绳子,一端固定在A轮边缘上,另一端系有重物P,当重物P以速率v匀速下落时,C轮转动的角速度为 。
12. 半径为10cm的砂轮,转速为5r/min,则砂轮旋转的角速度多大? 砂轮上距轴不同距离的点,角速度是否相等? 线速度是否相等? 砂轮边缘上的点的线速度多大?
13. 如图所示,皮带轮O1、O2的半径之比![]() ,A、B分别为轮
,A、B分别为轮![]() 边缘上的点,
边缘上的点,![]() ,求:A、B、C三点的向心加速度之比?
,求:A、B、C三点的向心加速度之比?
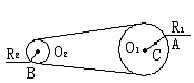
14. 地球表面赤道上的人和纬度45°处的人随地球自转的角速度之比为多少?线速度之比为多少?
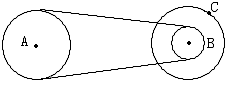
15. 如图所示,A轮通过皮带带动B轮,C轮与B轮同轴,已知RA:RB:RC=2:1:2,皮带传动时不打滑,试求:
(1)三轮边缘的线速度之比
(2)三轮的旋转周期之比
【试题答案】
1. B 2. BC 3. AC 4. AD 5.D 6. AD 7. C
8. ![]() ;
;![]() 9.
9. ![]()
10. ![]() 11.
11. ![]() 12.
12. ![]() ;是,不是,
;是,不是,![]()
13. ![]() 14.
14. ![]() ;
;![]() 15.(1)
15.(1)![]() (2)
(2)![]()