牛顿运动定律
(时间:60分钟 总分:100分)
一.选择题:(每题6分,共36分)
1.有两个分力,它们的大小是50N和30N,则这两个力的合力的大小 [ ]
A.可能等于50N B.可能等于30N
C.一定大于20N D.一定小于20N
2.一个物体受到多个力作用而保持静止,后来物体所受的各力中只有一个力逐渐减小到零后又逐渐增大 ,其它力保持不变,直至物体恢复到开始的受力情况,则物体在这一过程中 [ ]
A.物体的速度逐渐增大到某一数值后又逐渐减小到零
B.物体的速度从零逐渐增大到某一数值后又逐渐减小到另一数值
C.物体的速度从零开始逐渐增大到某一数值
D.以上说法均不对
3.质量为m1和m2的两个物体,分别以v1和v2的速度在光滑水平面上做匀速直线运 动,且v1<v2,如图所 示。如果用相同的水平力F同时作用在两个物体上,则使它们的速度相等的条件是 [ ]
![]()
A.力F与v1、v2同向,且m1>m2
B.力F与v1、v2同向,且m1<m2
C.力F与v1、v2反向,且m1>m2
D.力F与v1、v2反向,且m1<m2
4.如图所示,用大小相等,方向相反,并在同一水平面上的力N挤压相同的木板,木板中间夹着两块相 同的砖,砖和木板保持相对静止,则 [ ]
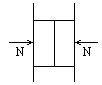
A.两砖间摩擦力为零
B.N越大,板和砖之间的摩擦力越大
C.板、砖之间的摩擦力大于砖重
D.两砖间没有相互挤压的力
5.如图所示,一根粗细均匀的金属棒放在光滑的水平面上,在水平向右的恒力F作用下做匀加速直线运 动,这时棒中自左向右的各横截面上的张力的大小 [ ]
![]()
A.都等于F B.逐渐增大但不会大于F
C.都为零 D.逐渐减小但不会小于F
6.如图所示,在光滑水平面上有一质量为M的斜劈,其斜面倾角为q,一质量为m的物体放在其光滑斜面 上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为[ ]
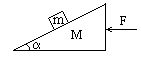
![]()
二.填空题(每空4分,共36分)
1.同一水平面内有3个力作用于一点,恰好平衡。已知F1与F2的夹角为90°,F2与F3的夹角为120°, 则3力之比为_________________。
2.如图所示,质量为m的小球B用一根长为L的细绳悬吊起来放在半径为R的光滑球面上,由悬点A到球面的最短距离AC=S,则小球对球面的压力为__________,细绳上的张力为_________。(小球的半径可 忽略不计)
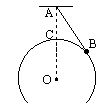
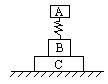
3.如图所示,木块A、B用一轻弹簧相连,竖直放在木块C上,C静置于地面上,它们的质量之比 是1:2:3,设所有接触面都光滑.当沿水平方向迅速抽出木块C的瞬间,A、B的加速度分别 是aA=________,aB=__________。

5.用平行于斜面的外力F,使静止的质量为m的物体在倾角为a的光滑斜面上,由底端向顶端做匀加速直线运动,当物体运动到斜面中点时,撤去外力F,物体刚好能到达斜面顶点,则外力的大小 为____________。
6.如图所示,在固定的光滑水平地面上有质量分别为m1和m2的木块A、B。A、B之间用轻质弹簧相连接,用水平向右的外力F推A,弹簧稳定后,A、B一起向右做匀加速直线运动,加速度为a,以向右为正方向,在弹簧稳定后的某时刻,突然将外力F撤去,撤去外力的瞬间,木块A的加速度是a1=_____,木块B的加速度是a2=_____。
![]()
三.计算题(1、2题各9分,3题10分)
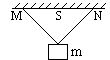
1.如图所示,两根长度相等的轻绳,下端悬挂一质量为m的物体,上端分别固定在水平天花板上的M、N点,M和N之间的距离为S。已知两绳所能经受的最大拉力均为T,则每根绳的长度不得短于多少?
2.如图所示,在劲度系数为k的弹簧下端挂一质量为m的物体,下面用托盘托着物体,使弹簧恰好维持原长,然后使托盘以加速度a(a<g)竖直向下做匀加速运动,则托盘与物体脱离所经历的时间是多少?
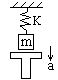
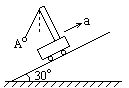
3.如图所示,质量为0.2kg的小球A用细绳悬挂于车顶板的O点,当小车在外力作
用下沿倾角为30°的斜面向上做匀加速直线运动时,球A的悬线恰好与竖直方向成
30°夹角。求:
(1)小车沿斜面向上运动的加速度多大?
(2)悬线对球A的拉力是多大?
单元练习题参考答案
一.
1.AB 2.C 3.BC 4.A 5.B 6.D
二.
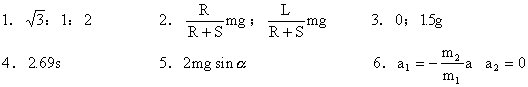
三.
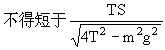
1.
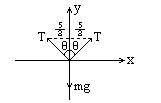
解:对物体m做受力分析,m受两绳拉力T,重力mg,
三个力合力为零,设每根绳长为L
![]()
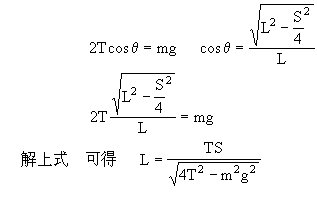
解:物体m在下降过程中,受力重力mg,弹力f =kx,
x为弹簧的伸长,在伸长0~x,内m受重力mg,
板的支持力N,三个力的合力产生的加速度正好等于a,
m与板一起以a向下做匀加速运动,
当x增大,f增大,N减小,
当N=0时,mg、f的合力产生加速度最大为a,
x再增大x>x0时,m的加速度小于a,
当x=x0时,
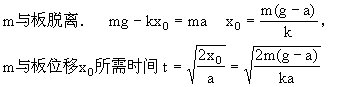
![]()
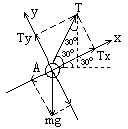
解:对球A做受力分析
A受两个力重力mg、绳子的拉力T
将二力沿图示x、y方向分解
x Tcos30°-mgsin30°=ma ①
y Tsin30°-mgcos30°=0 ②
![]()