鲁教版高一年物理复习——直线运动
知识重点:
1、掌握运动学的知识网络,对运动学有整体认识。
2、掌握匀变速直线运动的公式,知道它们是如何推导出的,有何联系,会应用这些公式分析和计算。
知识难点:
1、掌握运用匀变速直线运动的规律来解答习题的步骤。
2、通过对物理过程的分析,选用适当的公式列方程解决问题。
知识网络:

基本公式:
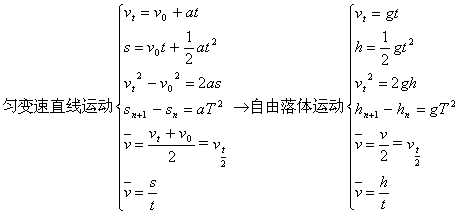
1. 匀变速直线运动的基本规律
(1)基本公式:![]()
![]()
![]()
(2)两个重要推论:![]()
![]() t
t
2. 匀变速直线运动的重要导出规律:
(1)任意两个相邻相等的时间间隔(T)内的,位移之差(△s)是一恒量,即
![]()
(2)在某段时间的中间时刻的速度等于这段时间内的平均速度,即![]()
(3)在某段位移中点位置的速度和这段位移的始、末瞬时速度的关系为
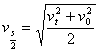
3. 初速度为零的匀变速直线运动的特点
(1)设T为单位时间,则有
①瞬时速度与运动时间成正比,![]()
②位移与运动时间的平方成正比,![]()
③连续相等的时间内的位移之比,![]()
(2)设S为单位位移,则有
①瞬时速度与位移的平方根成正比,![]()
②运动时间与位移的平方根成正比,![]()
③通过连续相等的位移所需的时间之比
![]()
解题步骤:
运用匀变速直线运动的规律来解答习题时,一般可分为以下几个步骤进行:
(1)根据题意,确定研究对象
(2)明确物体做什么运动,并且画出草图
(3)分析运动过程的特点,并选用反映其特点的公式
(4)建立一维坐标,确定正方向,列出方程求解
(5)进行验算和讨论
图象:
1、s-t图象
1)熟悉各种运动的s-t图象特征
2)计算单个物体的位移、速度
3)对比多个物体的位移、速度
4)确定多个物体的相对位置
注意:图象是数学图线而非物体的运动轨迹
2、v-t图象
1)熟悉各种运动的v-t图象特征
2)计算单个物体的位移、速度、加速度
3)对比多个物体的位移、速度、加速度
注意:除非题目特别交代,v-t图象无法确定物体间的相对位置
【典型例题】
例1、客车以20m/s的速度行驶,突然发现同轨前方120m处有一列货车正以6m/s的速度同向匀速前进,于是客车紧急刹车,刹车引起的加速度大小为0.8m/s2,问两车是否相撞?
解析:这是多个质点运动问题。两车不相撞的条件是:当客车减速到6m/s时,位移差△s=s货+s0-s客>0。
设客车刹车后经时间t两车速度相同。即v2=6(m/s)
![]()
此时两车相距为
![]()
=-2.5(m)
因为△s<0,故两车会相撞。
注意:该题中两车速度相等是一个临界状态,解答时应从这些特殊状态中寻找隐含条件,如本题中v2=6(m/s)这个条件。
例2、两木块自左向右运动,现有高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知
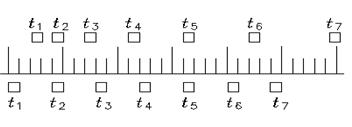
A. 在时刻t2以及时刻t5两木块速度相同
B. 在时刻t3两木块速度相同
C. 在时刻t3和时刻t4之间某瞬时两木块速度相同
D. 在时刻t4和时刻t5之间某瞬时两木块速度相同
分析:本题考查识图能力和分析能力。由图可知,上面一个木块在各个连续相等的时间间隔内通过的位移依次是:s1=2L,s2=3L,s3=4L,s4=5L……(L为标尺的分度)。由Δs=s2-s1=s3-s2=aT2知道,木块做匀加速直线运动,下面一个木块在连续相等的时间间隔内位移都等于s=4L,是匀速直线运动,从t3时刻到t4时刻,两木块位移相等,平均速度相等,对匀变速直线运动,某段时间中间时刻的瞬时速度等于该段时间内的平均速度,故两木块在t3~t4的中间时刻速度必然相等,而其他时刻速度均不相等。 答案:C
例3、某人在高100 m的塔顶,每隔0.5 s由静止释放一个金属小球.取g=10 m/s2,求:
(1)空中最多能有多少个小球?
(2)在空中最高的小球与最低的小球之间的最大距离是多少?(不计空气阻力)
解:由H=![]() gt2,那么第一个球从静止释放到着地的时间t=
gt2,那么第一个球从静止释放到着地的时间t=![]() s=4.47 s.则释放小球个数就是空中小球数.则n=
s=4.47 s.则释放小球个数就是空中小球数.则n=![]() ,对n取整数加1,所以N=8+1=9(个).
,对n取整数加1,所以N=8+1=9(个).
当最低球着地前的一瞬间,最低球与最高球之间有最大距离,则由h=![]() gt2=
gt2=![]() ×10×0.472 m=1.10 m,所以Δs=H-h=100 m-1.10 m=98.90m.
×10×0.472 m=1.10 m,所以Δs=H-h=100 m-1.10 m=98.90m.
【模拟试题】
1. 匀变速直线运动是 ( )
①位移随时间均匀变化的直线运动 ②速度随时间均匀变化的直线运动
③加速度随时间均匀变化的直线运动 ④加速度的大小和方向恒定不变的直线运动
A. ①② B. ②③ C. ②④ D. ③④
2. 汽车以5 m/s的速度在水平路面上匀速前进,紧急制动时以-2 m/s2的加速度在粗糙水平面上滑行,则在4 s内汽车通过的路程为 ( )
A. 4 m B. 36 m C. 6.25 m D. 以上答案都不对
3. 某质点的位移随时间的变化规律的关系是: s=4t+2t2,s与t的单位分别为m和s,则质点的初速度与加速度分别为 ( )
A. 4 m/s与2 m/s2 B. 0与4 m/s2
C. 4 m/s与4 m/s2 D. 4 m/s与0
4. 汽车刹车后做匀减速直线运动,经3 s后停止运动,那么,在这连续的3个1 s内汽车通过的位移之比为 ( )
A. 1∶3∶5 B. 5∶3∶1 C. 1∶2∶3 D. 3∶2∶1
5. 光滑斜面的长度为L,一物体由静止开始从斜面顶端沿斜面匀加速滑下,当该物体滑到底部时的速度为v,则物体下滑到L/2处的速度为 ( )
A. ![]() B.
v/2 C.
B.
v/2 C.
![]() D.
v/4
D.
v/4
6. 甲乙两个质点同时同地向同一方向做直线运动,它们的v—t图象如图所示,则前4s内 ( )
A. 乙比甲运动得快
B. 2 s末乙追上甲
C. 甲的平均速度大于乙的平均速度
D. 乙追上甲时距出发点40 m远
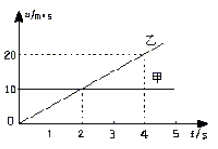
7. 一匀变速直线运动的物体,设全程的平均速度为v1,运动中间时刻的速度为v2,经过全程位移中点的速度为v3,则下列关系正确的是 ( )
A. v1>v2>v3 B. v1<v2=v3 C. v1=v2<v3 D. v1>v2=v38. 甲、乙、丙三辆汽车以相同的速度同时经过某一路标,从此时开始甲车一直做匀速直线运动,乙车先加速后减速,丙车先减速后加速,它们经过下个路标时速度又相同,则 ( )
A. 甲车先通过下一个路标 B. 乙车先通过下一个路标
C. 丙车先通过下一个路标 D. 条件不足,无法判断
9. 两辆完全相同的汽车,沿平直道路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停车时,后车以前车刹车时的加速度开始刹车.已知前车在刹车过程中行驶的路程为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离应为 ( )
A. s B. 2s C. 3s D. 4s
10. 某物体做直线运动的速度图象如图所示,则由图象可以判断出物体的运动情况是: ( )
A. 物体做往复运动,在每个周期内的运动轨迹都重合
B. 物体自始至终做匀变速直线运动
C. 物体一直沿某一方向做直线运动
D. 物体做往复运动,每经历一个周期,便向某一方向前进一段距离
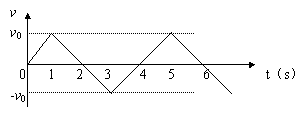
11. 火车以速度v1匀速行驶,司机发现前方同轨道上相距s处有另一火车沿同方向以速度v2(对地且v1>v2)做匀速运动,司机立即以加速度a紧急刹车。要使两车不相撞,a应满足什么条件。
12. 一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始行驶,恰在此时,一辆自行车以6m/s的速度匀速驶过,试求:
1)汽车从路口开动后,在追上自行车之前,经过多少时间两车距离最远?该最大距离为多少?
2)什么时候汽车追上自行车?此时汽车的速度多大?
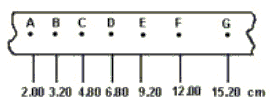
13. 如图所示,纸带上A、B、C、D、E、F、G为计数点,每相邻两个计数点间还有4个点没有画出,由图可知纸带的加速度等于 ,在打D点时纸带的速度为 .(图中表示各计数点与第一个点A的距离)
14. 从离地500m的空中自由落下一个小球,取g= 10m/s2,求小球:
1)经过多少时间落到地面;
2)从开始落下的时刻起,在第1s内的位移、最后1s内的位移;
3)落下一半时间的位移。
【试题答案】
1. C 2. C 3. C 4. B 5. A
6. D 7. C 8. B 9. B 10. A
11. a≥![]()
12. 2s、6m;4s、15m/s
13. 设A、B与B、C等各相邻计数点间的距离,依次为s1、s2、s3……,由图中给出的数据,则有
s1=3.20-2.00=1.20cm s2=4.80-3.20=1.60cm
s3=6.80-4.80=2.00cm s4=9.20-6.80=2.40cm
s5=12.00-9.20=2.80cm s6=15.20-12.00=3.20cm
因 s2-s1=s3-s2=s4-s3=s5-s4=s6-s5=Δs=0.40cm
故纸带做匀加速运动
T=5×0.02s=0.1s 由导出式 a=Δs/T2
故a=0.40×10-2/0.12m/s2=0.40m/s2
vD=sCE/2T=(9.20-4.80)×10-2/0.2m/s=0.22m/s
14.
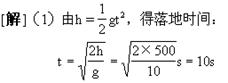
(2)第1s内的位移:
![]()
因为从开始运动起前9s内的位移为:
![]()
所以最后1s内的位移为:
h10=h-h9=500m-405m=95m
(3)落下一半时间即t'=5s,其位移为
![]()