08届高考数学综合训练(四)
1、已知函数![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的大小关系是 ( )
的大小关系是 ( )
A.![]() B.
B.![]()
C.![]() D.与
D.与![]() 和
和![]() 有关
有关
2、已知不等式![]() ,若对任意
,若对任意![]() 及
及![]() ,该不等式恒成立,则实数
,该不等式恒成立,则实数![]() 的范围是( )
的范围是( )
A ![]() B
B![]() C
C![]() D
D![]()
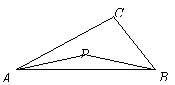
3、如图,设P为△ABC内一点,且![]() ,则△ABP的面积与△ABC的面积之比为 ( )
,则△ABP的面积与△ABC的面积之比为 ( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、已知A,B,C是平面上不共线上三点,O为![]() 外心,动点P满足
外心,动点P满足
![]()
![]() ,则P的轨迹定过
,则P的轨迹定过![]() 的 ( )
的 ( )
A 内心 B 垂心 C 重心 D AB边的中点
5、对任意实数![]() ,定义运算
,定义运算![]() ,其中
,其中![]() 为常数,等号右边的运算是通常意义的加、乘运算.现已知
为常数,等号右边的运算是通常意义的加、乘运算.现已知![]() 且有一个非零实数
且有一个非零实数![]() 使得对任意实数
使得对任意实数![]() ,都有
,都有![]() ,则
,则![]() = _____.
= _____.
 6、如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量
6、如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量![]() 围绕着点
围绕着点![]() 旋转了
旋转了![]() 角,其中
角,其中![]() 为小正六边形的中心,则
为小正六边形的中心,则![]() 。
。
7、代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以
8、在△ABC中,内角A、B、C的对边分别为![]() 、
、![]() 、
、![]() .其中
.其中![]() ,且
,且
![]() .
.
(1)求角B的大小;
(2)求![]() +
+![]() 的取值范围.
的取值范围.
9、已知函数![]()
![]() ,且函数
,且函数![]() 与
与![]() 的
的
图像关于直线![]() 对称,又
对称,又![]() ,
,![]() 。
。
1)求![]() 的表达式及值域;
的表达式及值域;
2)问是否存在实数m , 使得命题 ![]() 和
和![]()
满足复合命题 ![]() 且
且![]() 为真命题?若存在,求出m的取值范围;若不存在,说明理由.
为真命题?若存在,求出m的取值范围;若不存在,说明理由.
10、已知![]() ,P1(x1,y1)、P2(x2,y2)是函数
,P1(x1,y1)、P2(x2,y2)是函数![]() 图象上两点,且线段P1P2中点P的横坐标是
图象上两点,且线段P1P2中点P的横坐标是![]() 。
。
(1)求证:点P的纵坐标是定值;
(2)若数列![]() 的通项公式是
的通项公式是![]() …m),求数列
…m),求数列![]() 的前m项和Sm ;
的前m项和Sm ;
(3)在(2)的条件下,若![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
11、已知函数![]()
(1)求![]() 在[0,1]上的极值;
在[0,1]上的极值;
(2)若对任意![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在[0,1]上恰有两个不同的实根,求实数
在[0,1]上恰有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
12、已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(1)![]() ,求直线
,求直线![]() 、
、![]() 的方程。
的方程。
(2)设![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(3)在(2)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内总存在
内总存在![]() 个实数
个实数![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
南海中学2008届高三理科数学综合训练(四)参考答案
1-4 ABCD , 5、4 , 6、-1
7、2.5小时 【解题思路】:设台风中心开始时的位置为P,移动后(A码头受到台风影响时或影响结束时)的位置为Q,记![]() ,由题意得,
,由题意得,![]() ,解得
,解得![]() 或
或![]() ,则A码头从受到台风影响到影响结束时台风中心移动的距离为
,则A码头从受到台风影响到影响结束时台风中心移动的距离为
8、 解:(1)由![]() 得
得![]()
可知![]() ,否则有,
,否则有,![]() ,
,![]() ,互相矛盾.
,互相矛盾.
∴ ![]() ,即
,即![]() 而
而![]() ,所以
,所以![]() . ∴ B=
. ∴ B=![]() .
.
(2)由正弦定理有, ,∴
,∴ ![]() ,
, ![]() ,
,
∴![]()
∵ ![]() , ∴
, ∴ ![]() , 于是
, 于是![]() ,
,
则![]() +
+![]() 的取值范围是
的取值范围是![]() .
.
9、解 1)由![]() ,
,![]() 可得
可得![]() ,故
,故![]() ,
,
由于![]() 在
在![]() 上递减,所以
上递减,所以![]() 的值域为
的值域为![]()
(2)![]() 在
在![]() 上递减,故
上递减,故![]() 真
真![]()
![]() 且
且![]() ;
;
又![]() 即
即![]() ,故
,故![]() 真
真![]()
![]() ,
,
故存在![]() 满足复合命题
满足复合命题 ![]() 且
且![]() 为真命题。
为真命题。
10、解:(1)由![]() 知,x1+x2=1,则
知,x1+x2=1,则
![]()
![]()
故点P的纵坐标是![]() ,为定值。
,为定值。
(2)已知![]() …+
…+![]() …
…![]()
又![]() …
…![]() …
…![]()
二式相加,得
![]() …
…![]()
因为![]() …m-1),故
…m-1),故![]() ,
,
又![]() ,从而
,从而![]() 。
。
(3)由![]() 得
得![]() …①对
…①对![]() 恒成立。显然,a≠0,
恒成立。显然,a≠0,
(ⅰ)当a<0时,由![]() 得
得![]() 。而当m为偶数时
。而当m为偶数时![]() 不成立,所以a<0不合题意;
不成立,所以a<0不合题意;
(ⅱ)当a>0时,因为![]() ,则由式①得,
,则由式①得,![]()
又![]() 随m的增大而减小,所以,当m=1时,
随m的增大而减小,所以,当m=1时,![]() 有最大值
有最大值![]() ,故
,故![]() 。
。
11、解:(1)![]() ,令
,令![]() (舍去)
(舍去)
![]() 单调递增;当
单调递增;当![]() 单调递减.
单调递减.
![]() 上的极大值,没有极小值。
上的极大值,没有极小值。
(2)由![]() 得
得![]() ……①
……①
设![]() ,
,![]() ,
,
依题意知![]() 上恒成立,
上恒成立,
![]() ,
,
![]() ,
,
![]() 上单增,要使不等式①成立,
上单增,要使不等式①成立,
当且仅当![]()
(3)由![]()
令![]() ,
,
当![]() 上递增;
上递增;
当![]() 上递减 。
上递减 。
而![]() ,
,
![]() 恰有两个不同实根等价于
恰有两个不同实根等价于
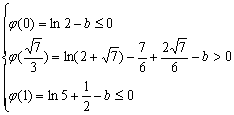
![]()
12、解:(1)设切点横坐标为![]() ,
,![]()
![]() ,
,
![]() 切线的方程为:
切线的方程为:![]() ,又
,又![]() 切线过点
切线过点![]() ,
,
![]() 有
有![]() ,即
,即![]() , 解得
, 解得![]()
![]() 切线
切线![]() 、
、![]() 的方程为:
的方程为:![]()
(2)设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,
,
![]()
![]() ,
, ![]() 切线
切线![]() 的方程为:
的方程为:![]() ,
,
![]() 切线
切线![]() 过点
过点![]() ,
, ![]() 有
有![]() ,
,
即![]() ,………① 同理,由切线
,………① 同理,由切线![]() 也过点
也过点![]() ,
,
得![]() .………②,由①、②,可得
.………②,由①、②,可得![]() 是方程
是方程![]() 的两根,
的两根,
 ………………………………………………………( * )
………………………………………………………( * ) 

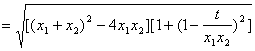 ,把( * )式代入,得
,把( * )式代入,得![]() ,
,
因此,函数![]() 的表达式为
的表达式为![]() .
.
(3)解法![]() :易知
:易知![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]()
![]()
![]() ,
,
则![]() .
.
依题意,不等式![]() 对一切的正整数
对一切的正整数![]() 恒成立,
恒成立, ![]() ,
,
即![]() 对一切的正整数
对一切的正整数![]() 恒成立,.
恒成立,.
![]() ,
, ![]() ,
,
![]() .由于
.由于![]() 为正整数,
为正整数,![]() .
.
又当![]() 时,存在
时,存在![]() ,
,![]() ,对所有的
,对所有的![]() 满足条件。
满足条件。
因此,![]() 的最大值为
的最大值为![]() .
.
解法![]() :依题意,当区间
:依题意,当区间![]() 的长度最小时,得到的
的长度最小时,得到的![]() 最大值,即是所求值.
最大值,即是所求值.
![]() ,
,![]() 长度最小的区间为
长度最小的区间为![]() ,
,
当![]()
![]() 时,与解法
时,与解法![]() 相同分析,得
相同分析,得![]() ,
,
解得![]() .
后面解题步骤与解法
.
后面解题步骤与解法![]() 相同(略).
相同(略).