08届高考教学第二次质量统一检测
数学试题（文科）
命题、审题：章 帆（株洲市四中） 叶美雄（南方中学） 曾辰晖（炎陵一中）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分，考试时间120分钟．
参考公式： http://www.mathedu.cn
如果事件A、B互斥，那么 正棱锥、圆锥的侧面积公式
如果事件A、B相互独立，那么 其中，c表示底面周长、l表示斜高或
母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P，那么n次独立重复实验中恰好发生k
次的概率
其中R表示球的半径
第Ⅰ卷（选择题）
一．选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合要求的．答案要写在答题卷上。
1、函数
的定义域是（
）
A、
B、
C、
D、
2、
垂直，则
等于(
)
A.
B. 1
C. 
D.
3、某单位有职工160人，其中有业务人员120人，管理人员16人，后勤人员24人，为了了解职工的某种情况，要从中抽取一个容量为20的样本，若要用分层抽样的方法抽取的业务人员、管理人员、后勤人员的人数分别为（ ）
（A） 7、6、7 （B） 15、2、3
（C） 10、6、4 （D） 17、1、2
4、已知
则
的值为（ ）
A．
B．
C．
D．
5、等差数列
中，若
，
，则前9项的和
等于（
）
A．66 B．99 C．144 D．297
6、关于直线
以及平面
，下面命题中正确的是（ ）
A．若
则
B．若
则
C．若
且
则 
D．若
则
7、函数
的图象过原点且它的导函数
的图象是
如图所示的一条直线, 则的图象的顶点在(
)
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
8、已知
则x,y之间的大小关系是（ ）
A.
B.
C.
D．不能确定
9、设A、B两点的坐标分别为(-1,0),(1,0)，条件甲：
； 条件乙：点C的坐标是方程 + = 1 (y¹0)的解. 则甲是乙的（ ）
（Ａ）充分不必要条件 （Ｂ）必要不充分条件
（Ｃ）充要条件 （Ｄ）既不是充分条件也不是必要条件
10、设数列
的前n项和为
，令
，称
为数列
，
，…，
的“理想数”，已知数列，，…，
的“理想数”为2004，那么数列8， ，，…，的“理想数”为 （
）
A．2008 B．2006 C． 2004 D． 2002
第Ⅱ卷（非选择题）
http://www.mathedu.cn
二、填空题：本大题共5小题，每小题5分 ，共25分，把答案填在答题卡中对应题号后的横线上.
11、
展开式中
的系数是_____________
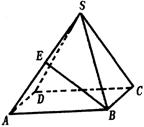
12、如图已知正四棱锥
侧棱长为
，底面边长为
，
是
的中点，则异面直线
与
所成角的大小为______________
13．有3个相识的人某天乘同一火车外出，假设火车有10节车厢，那么至少有2人在同一节车厢相遇的概率是________________
14、已知双曲线
，其左右焦点分别为F1、F2，圆C：
且
，则双曲线的离心率为________________
15、如果直线
与圆
相交于M、N两点，且点M、N关于直线
对称，动点
在不等式组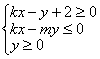
表示的平面区域的内部及边界上运动,则
(1)不等式组所确定的平面区域的面积为1;
(2)使得目标函数
取得最大值的最优解有且仅有一个;
(3)目标函数
的取值范围是
;
(4)目标函数
的最小值是
.
上述说法中正确的是
（写出所有正确选项）
三．解答题：本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16、(本题满分12分) ．
已知向量
，且与向量
所成角为
，其中A、B、C是△ABC的内角。（1）求角Ｂ的大小； （2）若
=1，AC=2，求△ABC的面积。
17、（本题满分12分）
设方程
，其中b、c
，
（1）求方程有实根的慨率；
（2）若函数
为偶函数，且
对
恒成立，
求
在
上的最大值。
18、（本题满分12分）
在直棱柱
中，
，
为棱
上一点，
，
为
的中点．
（1）、若E为线段AD上（不同于A、D）的任意一点，
求证：EF⊥
；
（2）、试问：若
，在线段
上的点能否使
与平面
成
的角？证明你的结论．
19、（本题满分12分）．
假设A型进口车关税税率在2002年是100％，在2007年是25％，2002年A型进口车每辆价格为64万元（其中含32万元关税税款）．
（1）已知与A型车性能相近的B型国产车，2002年每辆价格为46万元，若A型车的价格只受关税降低的影响，为了保证2007年B型车的价格不高于A型车价格的90％，B型车价格要逐年降低，问平均每年至少下降多少万元？
（2）某人在2002年将33万元存入银行，假设银行扣利息税后的年利率为1.8％（5年内不变），且每年按复利计算（上一年的利息计入第二年的本金），那么5年到期时这笔钱连本带息是否一定够买按（1）中所述降价后的B型车一辆？
20、（本小题满分13分）
已知函数
（1）当
时，证明
在
内是减函数；
（2）若在内有且只有一个极值点，求的取值范围。
21、（本题满分14分）
椭圆的中心是原点O，它的短轴长为
，相应于焦点F（c，0）（
）的准线
与x轴相交于点A，OF=2FA，过点A的直线与椭圆相交于P、Q两点。
（1）求椭圆的方程；
（2）若
，求直线PQ的方程；
（3）设
（
），过点P且平行于准线的直线与椭圆相交于另一点M，
证明
。
数学参考答案（文科）
一、选择题：（本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
| 题号 | 1 | ２ | ３ | ４ | ５ | ６ | ７ | ８ | ９ | １０ |
| 答案 | B | D | B | C | B | D | A | C | B | A |
二、填空题：（本大题共５小题，每小题５分，共２５分。把答案填写在相应的横线上。）
11、28； 12、
； 13、； 14、
； 15、（1）、（4）
三、解答题：（本大题共6小题，满分75分，解答要写出文字说明、证明过程或演算步骤）
16、解：（1）∵ , 且与向量所成角为
∴ 
，
∴ 
， ------------------3分
又
，∴
，即
。
-------------------6分
（2）由（1）可得：
∴ 
∵ 
， ∴ 
，
∴ 
，
∴ 当=1时，A=
---------10分
∴AB=2，
则
--------12分
17、解：（1）设事件A为方程有实根，由
得 
基本事件共有9种，事件A有6种，
∴
---------6分
（2）∵是偶函数，
∴b=c,即
又恒成立，即
对恒成立
∴
，∴c=3
∴
---------12分
18、解（1）连DF，AB＝AC，D为BC的中点
AD⊥BC，
直棱柱
平面
⊥平面ABC，
所以AD⊥平面，DF为EF在平面上的射影（*），因为BF＝BC＝
，BF∶
＝2∶1
＝BF＝BC＝BD，
所以Rt△DBF≌Rt△
，∠DFB＝∠
，
∠DFB＋∠
＝∠＋∠＝90°，
所以∠
＝90°，EF⊥
………………7分
（2）由（*）知∠EFD为EF与平面
成的角，若E为AD上一点，AB＝2a，
则tan∠EFD＝
，∠EFD＜60°，
即线段AD上的点E不能使EF与平面成60°的角 ………………12分
19、解：（1）2007年A型车价为32＋32×25％＝40（万元）
设B型车每年下降d万元，2002，2003……2007年B型车价格为：（公差为-d）
，
……
∴ ≤40×90％ ∴ 46-5d≤36 d≥2
故每年至少下降2万元 ………………6分
（2）2007年到期时共有钱
＞33（1＋0.09＋0.00324＋……）＝36.07692＞36（万元）
故5年到期后这笔钱够买一辆降价后的B型车 ………………12分
20、解：
………………2分
（1）
又
………………4分
由二次函数的图象可知，
时，恒有
在（－1，1）内是减函数
……………… 6分
（2）由于
若令
有
必有两个极值点
………………8分
要使在（－1，1）内只有一个极值点必须且只需
即
……………… 13分
21、解：（1）由题意，可设椭圆的方程为
。
由已知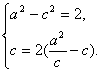得
解得
，
所以椭圆的方程为
。
……………… 4分
（2）由（1）可得A（3，0），设直线PQ的方程为
。由方程组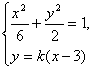
得
，依题意
，得
。
……………… 6分
设
，则
， ①，
。 ②
由直线PQ的方程得
。于是
。 ③
∵，∴
。 ④
由①②③④得
，从而
。
所以直线PQ的方程为
或
………… 9分
（3）证明：
。由已知得方程组
注意，解得
…………
12分
因
，故
。而
，
所以。
………… 14分