高考数学复习测试题一
姓名 得分
一.选择题.
1.设全集U = R ，A =
，则
UA=
（ ）．
A．
B.｛x x > 0｝ C.｛x x≥0｝ D.
≥0
2. 在数列1，2，2，3，3，3，4，4，4，4，……中，第25项为 （ ）．
A．25 B．6 C．7 D．8
3. 曲线
和直线
在y轴右侧的交点按横坐标从小到大依次记为P1，P2，P3，…，则P2P4等于
（ ）．
A．
B．2 C．3 D．4
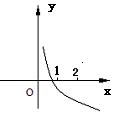4．右图为函数
的图象，其中m，n为常数，（ ）
则下列结论正确的是
A．
< 0 , n >1
B．> 0 , n > 1
C．> 0 , 0 < n <1 D． < 0 , 0 < n < 1
5.若 x、y 满足不等式组 ，则 2x + y 的取值范围是
(A) [,] (B) [－,] (C) [－,] (D) [－,]
6. 直线
绕原点按顺时针方向旋转30°所得直线与圆
的位置
关系是 （ ）
A．直线与圆相切 B．直线与圆相交但不过圆心
C．直线与圆相离 D．直线过圆心
7. 已知椭圆
与双曲线
有相同的焦点，则椭圆的离心率为
A． 
B． 
C． 
D．
（ ）
8.三位同学在研究函数 f (x)
= (x∈R) 时，分别给出下面三个结论：
① 函数
f (x) 的值域为 (－1,1)
② 若x1≠x2，则一定有f (x1)≠f (x2)
③ 若规定
f1(x)
= f (x)，fn+1(x) = f [ fn(x)]，则
fn(x) = 对任意 n∈N* 恒成立.
你认为上述三个结论中正确的个数有
（ ）
(A) 0个 (B)
1个 (C)
2个 (D)
3个
二.填空题.
9. 若双曲线的渐近线方程为
，它的一个焦点是
，则双曲线的方程是__________；
10. 已知函数
等于
；
11. 在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝, 第二件首饰是由6颗珠宝构成如图1所示的正六边形, 第三件首饰是由15颗珠宝构成如图2所示的正六边形, 第四件首饰是由28颗珠宝构成如图3所示的正六边形, 第五件首饰是由45颗珠宝构成如图4所示的正六边形, 以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断第6件首饰上应有_______________颗珠宝;则前
件首饰所用珠宝总数为__________________________颗.(结果用表示)
12. 若函数
内为增函数，则实数a的取值范围 ；
以下为选做题,请从中任选两题.
13.已知圆的直径AB=10cm，C是圆周上一点（不同于A、B点），CD
AB于D，CD=3cm，
则BD=_______________。
14.已知
为参数，则点(3，2)到方程
的距离的最大值是_____________。
15.已知x、y
R
，且4x+3y=1，则
＋
的最小值为______________。
三.解答题.
16.(12)已知函数
(
，
)为偶函数，且其图像上相邻的一个最高点和最低点之间距离为
.
⑴求
的解析式；
⑵若
，求
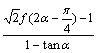的值。
17.(12) 已知
是定义在R上的函数，对于任意的实数a，b，都有
。
（Ⅰ）求
的值；
（Ⅱ）令
求证：
等差数列．
18. (14)某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额（最大供应量）如下表所示：
|
消耗量 资源 | 甲产品 （每吨） | 乙产品 （每吨） | 资源限额 （每天） |
| 煤（t） | 9 | 4 | 360 |
| 电力（kw·h） | 4 | 5 | 200 |
| 劳力（个） | 3 | 10 | 300 |
| 利润（万元） | 6 | 12 |
产品问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？
19.
（本小题满分14分）
设椭圆C：
的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且
.
⑴求椭圆C的离心率；
⑵若过A、Q、F三点的圆恰好与直线l：
相切，求椭圆C的方程.
20. （本小题满分14分）
已知
，
，数列
满足
，
， 
．
（Ⅰ）求证：数列
是等比数列；
（Ⅱ）当n取何值时，
取最大值，并求出最大值；
（III）若
对任意
恒成立，求实数
的取值范围．
21. （本小题满分14分）
已知
，点A(s,f(s)), B(t,f(t))
(I) 若
,求函数
的单调递增区间；
(II)若函数的导函数
满足：当x≤1时，有≤
恒成立，求函数的解析表达式；
(III)若0<a<b, 函数在
和
处取得极值，且
,证明：
与
不可能垂直.
高考数学复习测试题一
姓名： 得分
一.选择题.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 选项 |
|
|
|
|
|
|
|
|
二.填空题.
9． 10. 11. ；
12． 13． 14.
15.
三.解答题.
16.
17.
18.
19.
20.
21.
高考数学复习测试题一
答案
1. 答案：C. 
｛x x≥0｝,故选C.
2. 对于
中，当n＝６时，有
所以第２５项是７．选C.
3. Ａ． ∵
＝
，
∴根据题意作出函数图象即得．选A．
4. 答案：Ｄ．当x=1时，y＝m ,由图形易知m<0, 又函数是减函数，所以0<n<1,故选Ｄ．
5.C 6.Ｂ
7.D 由题意得，
又 
所以
8.D 9.
10.
11. 66, 
12.
13. 1cm或9cm
14. 
-1
15. 7+4
16. 解：⑴设最高点为
，相邻的最低点为
，则x1–x2=
∴
，∴
，∴
………………………（3分）
∴
， ∵是偶函数，∴
，
.
∵
，∴
，∴
…………… (6分)
⑵∵
，∴
………………………………(8分)
∴原式
……………………（12分）
17. 解：（1）令
………2分
由
（II）
设
………………………………………………9分
两边同乘以
故数列
等差数列 ……………………………………………12分
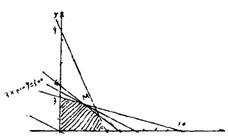
18. 解：设此工厂应分别生产甲、乙两种产品x吨y吨，获得利润z万元…………1分
|
…………………………5分
利润目标函数
………………………………8分
如图，作出可行域，作直线
向右上方平移至l1位置，直线经过可行域上的点M，且与原点距离最大，此时取最大值。……10分
解方程组
………………………………12分
所以生产甲种产品20t，乙种产品24t，才能使此工厂获得最大利润。……14分
19. 解⑴设Q（x0，0），由F（-c，0）
A（0，b）知
设
，
得
…2分
因为点P在椭圆上，所以
…………4分
整理得2b2=3ac，即2(a2－c2)=3ac，
,故椭圆的离心率e=
………6分
⑵由⑴知
， 
于是F（－a，0） Q
，
△AQF的外接圆圆心为（a，0），半径r=FQ=a……………………11分
所以
，解得a=2，∴c=1，b=，所求椭圆方程为
……14分
20. 解：（I）∵，
，
，
∴
． 即
．
又，可知对任何
，
，所以
．………2分
∵
，
∴是以
为首项，公比为
的等比数列．………4分
（II）由（I）可知
=
（
）．
∴
．
．……………………………5分
当n=7时，
，
；当n<7时，
，
；
当n>7时，
，
．
∴当n=7或n=8时，取最大值，最大值为
．……8分
（III）由，得
（*）
依题意（*）式对任意恒成立，
①当t=0时，（*）式显然不成立，因此t=0不合题意．…………9分
②当t<0时，由
，可知
（）．
而当m是偶数时
，因此t<0不合题意．…………10分
③当t>0时，由（）,
∴
∴
． （）……11分
设
（）
∵
=
,
∴
．
∴
的最大值为
．所以实数
的取值范围是
．………13分
21.解：(I) f (x)=x3-2x2+x,
(x)=3x2-4x+1,
因为f(x)单调递增，
所以(x)≥0，
即 3x2-4x+1≥0,
解得，x≥1, 或x≤
,……………………………2分
故f(x)的增区间是(-∞，)和[1,+ ∞]. …………………………3分
(II) (x)=3x2-2(a+b)x+ab.
当x∈[-1，1]时，恒有(x)≤.………………………4分
故有
≤(1)≤，
≤(-1)≤，
≤(0)≤,………………………5
即
………6
①+②，得
≤ab≤， 又由③，得ab=，
将上式代回①和②，得a+b=0,
故f(x)=x3x. ……………………9分
(III) 假设⊥,
即
=
= st+f(s)f(t)=0, ……………10分
(s-a)(s-b)(t-a)(t-b)=-1,
[st-(s+t)a+a2][st-(s+t)b+b2]=-1, ……………………………………11分
由s，t为(x)=0的两根可得，
s+t=
(a+b), st=, (0<a<b), 从而有ab(a-b)2=9. …………………………12分
这样(a+b)2=(a-b)2+4ab
= 
+4ab≥2
=12，即 a+b≥2,
这样与a+b<2矛盾. ……………………13分
故与不可能垂直. …………………………14分