08届高考理科数学第四次月考试题
数学试题(理科)
一、选择题:本题共12个小题,每小题5分,共60分。在每个小题的四个选项中,只有一项是符合题目要求的。
1.集合M![]() ,则M
,则M![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知向量a![]() ,若向量
,若向量![]() 与
与![]() 垂直,则
垂直,则![]() 的值为 ( )
的值为 ( )
A.![]() B.7 C.
B.7 C.![]() D.
D.![]()
3.设![]() 且
且![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知直线![]() 与
与![]() 互相垂直,垂足为
互相垂直,垂足为![]() ,则
,则![]() 的值是 ( )
的值是 ( )
A.24 B.20 C.0 D.-4
5.实数x,y满足不等式组 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
7.设a,b,c表三条直线,![]() 表示两个平面,则下列命题中逆命题不成立的是 ( )
表示两个平面,则下列命题中逆命题不成立的是 ( )
A.![]() ,若
,若![]() ,则
,则![]()
B.![]() ,
,![]() ,若
,若![]() ,则
,则![]()
C.![]() ,若
,若![]() ,则
,则![]()
D.![]() ,
,![]() 是
是![]() 在
在![]() 内的射影,若
内的射影,若![]() ,则
,则![]()
8.已知函数![]() 图象上A处的切线与
图象上A处的切线与![]() 的夹角为45
的夹角为45![]() ,则点A的横坐标是 ( )
,则点A的横坐标是 ( )
A.0 B.1 C.0或![]() D.1或
D.1或![]()
9.已知双曲线![]() ,被方向向量为
,被方向向量为![]() 的直线截得的弦的中点为(4,1),则该双曲线离心率的值是 ( )
的直线截得的弦的中点为(4,1),则该双曲线离心率的值是 ( )
|
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设正方体ABCD-A1B1C1D1中E,F分别是棱A1A,B1B中点,G为BC上一点,若C1F⊥EG,则![]() 为 ( )
为 ( )
A.60 ![]() B.
B.![]() C.120
C.120![]() D.150
D.150![]()
![]()
![]()
![]() 12.已知A,B是抛物线
12.已知A,B是抛物线![]() 上的两个点,O为坐标原点,若
上的两个点,O为坐标原点,若![]() 且
且![]() 的垂心恰是抛物线的焦点,则直线AB的方程是 ( )
的垂心恰是抛物线的焦点,则直线AB的方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
13.圆![]() 为参数)的标准方程是
,过这个圆外一点P
为参数)的标准方程是
,过这个圆外一点P![]() 的该圆的切线方程是
。
的该圆的切线方程是
。
14.若角![]() ________________
________________
15.已知m,n,m+n成等差数列,m,n,mn成等比数列,则椭圆![]() _______
_______
16.等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() __________.
__________.
三、解答题:本题共6个小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本题满分10分)
设有关于x的不等式![]()
![]()
(1)![]()
(2)当a为何值时,此不等式的解集为R(本题满分12分)
18.(本题满分10分)
已知角![]() 为
为![]() 的三个内角,其对边分别为
的三个内角,其对边分别为![]() ,若
,若![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() 的面积
的面积![]() ,求
,求![]() 的值.
的值.
(2)求![]() 的取值范围.
的取值范围.
19.(本小题满分12分)
|
已知椭圆![]() 是椭圆上纵坐标不为零的两点,若
是椭圆上纵坐标不为零的两点,若![]() 其中F为椭圆的左焦点.
其中F为椭圆的左焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)求线段AB的垂直平分线在y轴上的截距的取值范围.
20.(本题满分12分)
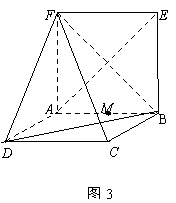 矩形ABCD与矩形ABEF的公共边为AB,且平面ABCD
矩形ABCD与矩形ABEF的公共边为AB,且平面ABCD![]() 平面ABEF,如图3所示,FD
平面ABEF,如图3所示,FD![]() , AD=1, EF=
, AD=1, EF=![]() .
.
(Ⅰ)证明:AE ![]() 平面FCB;
平面FCB;
(Ⅱ)求异面直线BD与AE所成角的余弦值
(Ⅲ)若M是棱AB的中点,在线段FD上是
否存在一点N,使得MN∥平面FCB?
证明你的结论.
21.(本题满分12分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上,且过点
的图像上,且过点![]() 的切线的斜率为
的切线的斜率为![]() .
.
(1)求数列![]() 的通项公式.
的通项公式.
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(3)设![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,
中的最小数,![]() ,求
,求![]() 的通项公式.
的通项公式.
22.(本题满分14分)
过双曲线![]() 的上支上一点
的上支上一点![]() 作双曲线的切线交两条渐近线分别于点
作双曲线的切线交两条渐近线分别于点![]() .
.
(1)求证:![]() 为定值;
为定值;
(2)若![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
参考答案
1.C 2.A 3.C 4.B 5.A 6.B 7.C 8.C 9.A 10.C 11.B 12.C
|
|
14.![]() 15.
15.![]() 16.n=12
16.n=12
17.(本小题满分10分)
解:![]() 时,不等式可化为
时,不等式可化为![]() …………………………… 2分
…………………………… 2分
由![]() ……………………………………………..4分
……………………………………………..4分
![]() …………………………………………………………5分
…………………………………………………………5分
![]()
![]() …………………………………………………………….7分
…………………………………………………………….7分
欲使![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
只须![]() 即可
即可![]()
![]() ……………………………………………………….. 10分
……………………………………………………….. 10分
18.(本小题满分10分)
解:(1)![]() ,
,![]() ,且
,且![]() .
.
![]() ,即
,即![]() ,又
,又![]() ,
,![]() ………..2分
………..2分
又由![]() ,
,![]()
由余弦定理得:![]()
![]() ,故
,故![]() …………………………………………………. 5分
…………………………………………………. 5分
(2)由正弦定理得: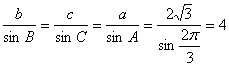 ,又
,又![]() ,
,
![]() ………………8分
………………8分
![]() ,则
,则![]() .则
.则![]() ,即
,即![]() 的取值范围是
的取值范围是![]() …………………………………………………………………………………10分
…………………………………………………………………………………10分
19.(本小题满分12分)
(Ⅰ)由已知,得
 ………4分
………4分
(Ⅱ)∵A、B是椭圆上纵坐标不为零的点,![]()
∴A、F、B三点共线,且直线AB的斜率存在且不为0.
又F(-1,0),则可记AB方程为![]() 并整理得
并整理得
![]() ……………………………………6分
……………………………………6分
显然△>0,设![]()
![]() ……………………8分
……………………8分
直线AB的垂直平分线方程为![]()
令x=0,得 ……………………………………10分
……………………………………10分
∵![]() “=”号,
“=”号,
∴![]() ,
,
所以所求的取值范围是![]() ……………………………………12分
……………………………………12分
 20.(本小题满分12分)
20.(本小题满分12分)
(1) ![]() 平面ABCD
平面ABCD![]() 平面ABEF,
平面ABEF,
且四边形ABCD与ABEF是矩形,
![]() AD
AD![]() 平面ABEF,
平面ABEF,![]() AD
AD![]() AE,
AE,
![]() BC∥AD
BC∥AD ![]() BC
BC![]() AE
AE
又FD=2,AD=1,所以AF=EF=![]() ,
,
所以四边形ABEF为正方形.![]() AE
AE![]() FB,
FB,
又BF![]() BF
BF![]() 平面BCF,BC
平面BCF,BC![]() 平面BCF
平面BCF
所以AE![]() 平面BCF……………………………………………4分
平面BCF……………………………………………4分
(2)设BF![]() AE=O,取FD的中点为H,连接OH,在
AE=O,取FD的中点为H,连接OH,在![]() OH//BD,
OH//BD,
![]()
![]() HOF即为异面直线BD与AE所成的角(或补角),
HOF即为异面直线BD与AE所成的角(或补角),
在![]() 中,OH=1,FH=1,FO=
中,OH=1,FH=1,FO=![]() ,
,![]() cos
cos![]() HOF=
HOF=![]()
![]() 异面直线BD与AE所成的角的余弦值为
异面直线BD与AE所成的角的余弦值为![]() ………………………….8分
………………………….8分
(3)当N为FD的中点时, MN∥平面FCB
证明:取CD的中点G,连结NG,MG,MN,
则NG//FC,MG//BC,
又NG![]() 平面NGM,MG
平面NGM,MG![]() 平面NGM且NG
平面NGM且NG![]() MG=G
MG=G
所以平面NGM//平面FBC,
![]() MN
MN![]() 平面NGM
平面NGM
![]() MN//平面FBC……………………………………………………………12分
MN//平面FBC……………………………………………………………12分
21.(本小题满分12分) 解:(1)![]() 点
点![]() 都在函数
都在函数![]() 的图像上,
的图像上,![]()
![]() ,
,
当![]() 时,
时,![]()
当n=1时,![]() 满足上式,所以数列
满足上式,所以数列![]() 的通项公式为
的通项公式为![]() …….3分
…….3分
(2)由![]() 求导可得
求导可得![]()
![]() 过点
过点![]() 的切线的斜率为
的切线的斜率为![]() ,
,![]() .
.
![]() .
.
![]() ①
①
由①×4,得
![]() ②
②
①-②得:
![]()
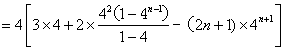
![]() ………………………………………………………………..7分
………………………………………………………………..7分
(3)![]() ,
,![]() .
.
又![]() ,其中
,其中![]() 是
是![]() 中的最小数,
中的最小数,![]() .
.
![]() 是公差是4的倍数,
是公差是4的倍数,![]() .
.
又![]() ,
,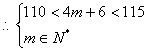 ,解得m=27.
,解得m=27.
所以![]() ,
,
设等差数列的公差为![]() ,则
,则![]()
![]() ,所以
,所以![]() 的通项公式为
的通项公式为![]() …………12分
…………12分
22.(本小题满分14分)
解:(1)设直线AB:![]()
由 得
得![]()
 …………………………………….3分
…………………………………….3分

…………………………………………………………………………………………….7分
(2)![]() ,所以四边形BOAM是平行四边形
,所以四边形BOAM是平行四边形
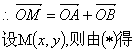 ……………………………………………………………….9分
……………………………………………………………….9分
![]() ①
①
![]() ②
②
由①②及![]() ……………………………………………..13分
……………………………………………..13分
![]() …………14分
…………14分
