08届高考文科数学复习第四次月考试题
数学试卷(文)
时量:120分钟 满分: 150分
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各式中,值为![]() 的是( )
的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 2.如图,
2.如图,![]() 为正方体,下面结论错误的是( )
为正方体,下面结论错误的是( )
(A)![]() 平面
平面![]()
(B)![]()
(C)![]() 平面
平面![]()
(D)异面直线![]() 与
与![]() 所成的角为60°
所成的角为60°
3.在等比数列![]() (
(![]() )中,若
)中,若![]() ,
,![]() ,则该数列的前10项和为( )
,则该数列的前10项和为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
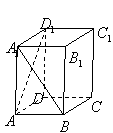 4.如图,正四棱柱
4.如图,正四棱柱![]() 中,
中,![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的余弦值为( )
所成角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设![]() 为两条直线,
为两条直线,![]() 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A.若![]() 与
与![]() 所成的角相等,则
所成的角相等,则![]()
B.若![]() ,
,![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,
,![]() ,则
,则![]()
D.若![]() ,
,![]() ,
,![]() ,则
,则![]()
6.如果双曲线![]() 上一点
上一点![]() 到双曲线右焦点的距离是2,那么点
到双曲线右焦点的距离是2,那么点![]() 到
到![]() 轴的距离是( )
轴的距离是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.设![]() 是
是![]() 和
和![]() 的等比中项,则
的等比中项,则![]() 的最大值为( )
的最大值为( )
A.1 B.3 C.![]() D.
D.![]()
8.给出下列三个等式:![]() ,
,![]() ,
, ![]() ,下列函数中不满足其中任何一个等式的是( )
,下列函数中不满足其中任何一个等式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
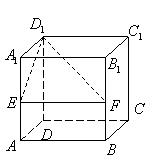 9.在棱长为1的正方体
9.在棱长为1的正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() .则点
.则点![]() 到平面
到平面![]() 的距离为( )
的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
10.已知抛物线![]() 上存在关于直线
上存在关于直线![]() 对称的相异两点
对称的相异两点![]() 、
、![]() ,则
,则![]() 等于( )
等于( )
(A)3
(B)4
(C)![]() (D)
(D)![]()
二、填空题:本大题共5小题,每小题5分 ,共25分,把答案填在答题卡中对应题号后的横线上.
11.数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于_____
等于_____
12. 若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() .
.
13.以双曲线![]() 的中心为顶点,且以该双曲线的右焦点为焦点的抛物线方程是________
的中心为顶点,且以该双曲线的右焦点为焦点的抛物线方程是________
14.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为![]() ,
,![]() ,
,![]() ,则此球的表面积为 .
,则此球的表面积为 .
15.已知正方形![]() ,则以
,则以![]() 为焦点,且过
为焦点,且过![]() 两点的椭圆的离心率为______.
两点的椭圆的离心率为______.
三.解答题:本大题共6小题,共75分. 解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,![]() .
.
(Ⅰ)求B的大小;
(Ⅱ)若![]() ,
,![]() ,求b.
,求b.
17. (本小题满分12分)
如图,在底面为平行四边形的四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
 (Ⅰ)求证:
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
18.(本小题满分12分)
设数列![]() 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,![]() 为等比数列,且
为等比数列,且![]()
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前n项和Tn
的前n项和Tn![]()
19. (本小题满分13分)
已知函数![]() ,常数
,常数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]()
(2)讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
20. (本小题满分13分)
如图,一载着重危病人的火车从O地出发,沿射线OA行驶,其中
![]() 在距离O地5a(a为正数)公里北偏东β角的N处住有一位医学专家,其中sinβ=
在距离O地5a(a为正数)公里北偏东β角的N处住有一位医学专家,其中sinβ= ![]() 现有110指挥部紧急征调离O地正东p公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车,并在C处相遇,经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时,抢救最及时.
现有110指挥部紧急征调离O地正东p公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车,并在C处相遇,经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时,抢救最及时.
|
(2)当p为何值时,抢救最及时.
21. (本小题满分13分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(![]() )的准线
)的准线![]() 与x轴相交于点A,OF=2FA,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,OF=2FA,过点A的直线与椭圆相交于P、Q两点.
(Ⅰ)求椭圆的方程及离心率;
(Ⅱ)若![]() ,求直线PQ的方程;
,求直线PQ的方程;
(Ⅲ)设![]() (
(![]() ),过点P且平行于准线
),过点P且平行于准线![]() 的直线与椭圆相交于另一点M,证明:
的直线与椭圆相交于另一点M,证明:![]() .
.
数学试卷(文)
参考答案
一、选择题
1、B 2、D 3、B 4、D 5、D 6、A 7、C 8、B 9、D 10、C
二、填空题
11、![]() 12、
12、![]() 13、
13、![]()
![]() 14、
14、![]() 15、
15、![]()
三、解答题
16、解:
(Ⅰ)由![]() ,根据正弦定理得
,根据正弦定理得![]() ,所以
,所以![]() ,
,
由![]() 为锐角三角形得
为锐角三角形得![]() .………………………..6分
.………………………..6分
(Ⅱ)根据余弦定理,得![]()
![]()
![]() .
.
所以,![]() .………………………………………………12分
.………………………………………………12分
17、(Ⅰ)∵PA⊥平面ABCD
∴AB是PB在平面ABCD上的射影
 又∵AB⊥AC,AC
又∵AB⊥AC,AC![]() 平面ABCD,
平面ABCD,
∴AC⊥PB……………………3分
(Ⅱ)连接BD,与AC相交于O,连接EO。
∵ABCD是平等四边形,
∴O是BD的中点,
又E是PD的中点,
∴EO∥PB
又PB![]() 平面AEC,EO
平面AEC,EO![]() 平面AEC,
平面AEC,
∴PB∥平面AEC。………………….7分
(Ⅲ)取BC中点G,连接OG,则点G的坐标为![]()
又![]()
∴![]()
∴OE⊥AC,OG⊥AC
∴∠EOG是二面角E-AC-B的平面角。
∵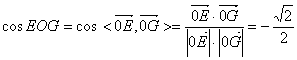
∴![]()
∴二面角![]() 的大小为
的大小为![]() …………………………….12分
…………………………….12分
18、
解:(1):当![]()
![]()
故{an}的通项公式为![]() 的等差数列.
的等差数列.
设{bn}的通项公式为![]()
故![]() ……….5分
……….5分
(II)
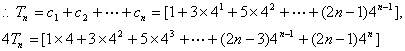
两式相减得
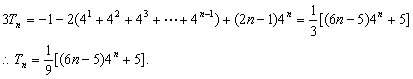
……………………………..12分
19、解:(1)![]() …………………………6分
…………………………6分
(2)当![]() 时,
时,![]() ,
,
对任意![]() ,
,![]() ,
, ![]() 为偶函数.
为偶函数.
当![]() 时,
时,![]() ,
,
取![]() ,得
,得 ![]() ,
,
![]() ,
,
![]() 函数
函数![]() 既不是奇函数,也不是偶函数. ……………………….13分
既不是奇函数,也不是偶函数. ……………………….13分
20、解:(1)以O为原点,正北方向为y轴建立直角坐标系,
则![]()
设N(x0,y0),![]()
![]()
又B(p,0),∴直线BC的方程为:![]()
由 得C的纵坐标
得C的纵坐标![]() ,∴
,∴![]() …………………6分
…………………6分
(2)由(1)得 ∴
∴![]() ,∴当且仅当
,∴当且仅当![]()
![]() 时,上式取等号,∴当
时,上式取等号,∴当![]() 公里时,抢救最及时.
公里时,抢救最及时.
…………………13分
21、(Ⅰ)解:由题意,可设椭圆的方程为![]() .由已知得
.由已知得 解得
解得![]() 所以椭圆的方程为
所以椭圆的方程为![]() ,离心率
,离心率![]() …………………………………………………………..3分
…………………………………………………………..3分
(Ⅱ)解:由(1)可得A(3,0).设直线PQ的方程为![]() .由方程组
.由方程组
 得
得![]() 依题意
依题意![]() ,得
,得![]() .设
.设![]() ,则
,则![]() , ①
, ①
![]() . ② 由直线PQ的方程得
. ② 由直线PQ的方程得![]() .于是
.于是
![]() . ③ ∵
. ③ ∵![]() ,∴
,∴![]() . ④. 由①②③④得
. ④. 由①②③④得![]() ,从而
,从而![]() .
.
所以直线PQ的方程为![]() 或
或![]() . ……………………..7分
. ……………………..7分
(Ⅲ)证明:![]() .由已知得方程组
.由已知得方程组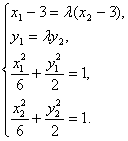
注意![]() ,解得
,解得![]() . 因
. 因![]() ,
,
故![]()
![]() .
.
而![]() ,所以
,所以![]() .
.
……………………………….13分
