08届高考文科数学第一次模拟考试试卷
命题人。粱宪平 江国华 (景德镇一中)仇裕玲（鹰潭一中）
审题人：武智理曹永泉（景德镇一中）
考生注意：
1．本考试设试卷Ⅰ卷、Ⅱ卷和答题纸三部分，试卷包括试题与答题要求，所有答题必须写在答题纸上，做在试卷上一律不得分。
2．答题纸与试卷在试题编号上是一一对应的，答题时应特别注意，不能错位。
3．考试时间120分钟。试卷满分150分。
第Ⅰ卷(选择题，共60分)
一、选择题：(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求)
1．已知全集U=Z，A={－2，－1，0，1}，B={x 
，x∈Z}，则
( )
A、{0，1｝ B、｛1｝ C、{－2，－1} D、｛－1,0，1}
2．己知α∈(
，π)，sinα=
，则tan(α+
)的值为( )
A、7 B、－
D、－
3．在△ABC中，已知D是AB边上一点，若
，
，则λμ=( )
A、
B、
C、－ D、－
 |
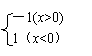4．设函数f(x)＝ ,则
的值为
A、a B、b C、min{a，b}．D、max{a，b}
5．
的展开式中的常数项是( )
A、15 B、－
6．已知定义在R上的函数y=f(x)存在反函数y= f－1(x)，若函数y=f(x+1)的反函数是f－1(x－1)，且f(0)＝1，则f(12)=
A、1 B、一
7．在△ABC中，设命题p：
，命题q：△ABC为等边三角形，那么命题p是命题q的( )
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
8．若直线y=kx+1与圆x2+y2=1相交于P、O两点，且∠POQ=60°(其中O为原点)，则k
的值为( )
A、
B、
C、
D、±
9．顶点往同一球面上的正四棱柱ABCD－A′B′C′D中，AB=1，AA′=
，则A、C两点间的球面距离为( )
A、
B、 C、
D、
10．12支足球队(含甲、乙、丙)平均分成三个小组，甲、乙、丙三个球队中至少有两支球队被分在同一小组的概率是( )
A、 B、
C、
D、
11．在三棱锥P—ABC中，∠APB=∠BPC=60°，PA=1，PB =
，PC=，则三棱锥P—ABC的体积为( )
A、
B、
C、
D、
12．椭圆C1：
的左准线为l，左、右焦点为分别为F1、F2，抛物线C2的准线为l，焦点为F2，C1与C2的一个交点为P，线段PF2的中点为G，O是坐标原点，则
的值为（ ）
A、－1 B、
D、
第Ⅱ卷(非选择题，共90分)
二、填空题(本大题共4小题，每小题4分，共16分，把答案填在答题卡上的相应位置)
13．某学校举行师生座谈会，采用分层抽样的方法邀请部分师生代表参加，已知老师代表与学生代表的比为4：5，其中学生代表中男生是女生人数的
，且男生代表比女生代表多3人，则参加座谈的老师代表共有
14．设0<a<1，且m=loga(a2+1)，n=loa（a+1)，P=loga(2a)，则m、n、P的大小为
(用“>”号连接)
15．已知在平面直角坐标系中O(0，0)、M(1，0)、N(1，1)、Q(2，3)动点P(x，y)满足不等式1≤
≤3，2 ≤
≤4，则ω=
的最大值为
16．有下列命题：
①若sin θ+cosθ=，则
②关于实数x的方程sinx=x有三个解：
③若角，β满足cosα cosβ=1，则sin(α+β)=0；
④函数f(x)=sinx+sinx 的值域为[－2，2]；
其中正确的命题序号是
三、解答题
17．(本小题满分12分)已知函数f(x)＝(4cos2x－2)(cos 2x+2sinxcosx)－1，
(1)求 f(x)的最小正周期；
(2)在给出的直角坐标系中画出y= f(x) 在区间[－
，
]上的简图．(要求先列表，再描点画图)
18．(本小题满分12分)已知函数f(x) ＝ax3+bx2+cx+d(x∈R)在x=时取极小值－6，且函数y＝f(x＋)的图象关于点(－，0)对称．
(1)判断函数 f(x)的奇偶性并求f(x)的解析式：
(2)x∈[－2，1]时，求f(x)的值域；
19．(本小题满分12分)如图，已知梯形ABB1E中EB1∥AB和正方形BB1 C1C且AC=BlCl=2，
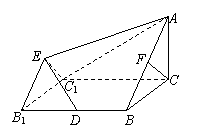CCl⊥平面EBlCl，D是BBl的中点，F是AB的中点，∠ACB=∠AED=90°
(1)求证CF⊥平面ABBlE；
(2)求异面直线AC与ECl所成的角的大小；
(3)求二面角E—AC1—C的大小：
20．（本小题满分12分)设b，c分别是先后抛掷一枚骰子得到的点数，A＝｛xx2－bx+2c<0，x∈D}．
(1)若D=R，求A≠φ的概率：
(2)若D=N*，求A中恰有5个元素的概率：
21．(本小题满分12分)已知直线l：x一
+4=0与椭圆C：
(a>0，b>0)有且仅有一个公共点G，直线l与x轴交于E点，直线l与y轴交于F点，且
(1)求椭圆C的方程：
(2)若直线m绕点E旋转，且保持与(1)中所求的椭圆C相交于不同两点A、B，求直线m斜率的取值范围．
22．(本小题满分14分)已知数列{bn}中，bl= a，b2=a2，其中a>0，且a≠1，当n≥2时，总有bn+1=(1+a) bn－a bn－1
(1)求数列{bn}的通项公式：
(2)若
求数列{Cn }的前n项和Sn
